
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
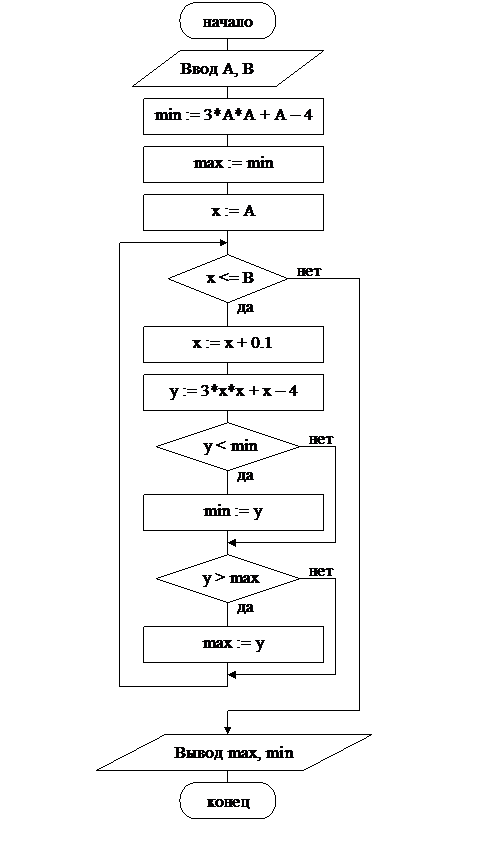
Текст программы на языке ПаскальProgram Example_6; Var A, B, R : word; Begin writeln; write(‘Введите натуральное число A = ‘); read(A); write(‘Введите натуральное число B = ‘); read(B); if A < B then R := B – 1 else R := A – 1; repeat R := R + 1 until (R mod A = 0) and (R mod B = 0); writeln(R, ‘ - наименьшее общее кратное чисел ‘, A, ‘ и ’, В); readln end. Данные для тестирования 1) Для А = 5, В = 3 ð 15 - наименьшее общее кратное чисел 5 и 3 2) Для А = 5, В = 30 ð 30 - наименьшее общее кратное чисел 5 и 30 3) Для А = 10, В = 25 ð 50 - наименьшее общее кратное чисел 10 и 25 Пример 3.2. Найти наибольшее и наименьшее значение функции y = 3x2 + x – 4, если на заданном отрезке [А, В] значения х изменяются с шагом 0,1. Математическая модель задачи Введём переменные: min – наименьшее значение функции; max – наибольшее значение функции; х – значение узла сетки, изменяющееся от А до В с шагом 0,1; у – значение заданной функции в узле сетки х. В качестве начального значения для переменных max и min примем значение функции в точке А. Далее с помощью цикла while и условного оператора организуем сравнение переменных max и min со значением функции в очередном узле сетке и, при необходимости, переприсваивание новых значений функции. Блок-схема алгоритма
Текст программы на языке Паскаль Program Example_7; Var A, B, x, y, max, min : real; Begin writeln; write(‘Введите начало отрезка A = ‘); read(A); write(‘Введите конец отрезка B = ‘); read(B); min := 3*A*A + A – 4; max := min; x := A; while x <= B do begin x := x + 0.1; y := 3*x*x + x – 4; if y < min then min := y; if y > max then max := y end; writeln(min, ‘ - наименьшее значение функции на отрезке [A, В]’); writeln(max, ‘ - наибольшее значение функции на отрезке [A, В]’); readln end. Данные для тестирования
Пример 3.3. Дано натуральное n. Вычислить сумму
Решение задачи Введём переменные: S – сумма; k – номер очередного слагаемого; n– количество слагаемых в сумме. Данная сумма может быть представлена в виде S=u1+u2+u3+… . Начальное значение суммы равно 0. При вычислении суммы к начальному ее значению прибавляется значение первого члена последовательности, затем к полученному значению прибавляется значение второго члена последовательности и так далее. То есть при вычислении суммы циклически проводится операция сложения. Вычисление суммы организуем с помощью цикла while. Если до начала цикла k присвоить 1, то в качестве условия выполнения цикла можно записать k <= n. Блок-схема алгоритма
Текст программы на языке Паскаль Program Example_8; Var k, n : integer; S : real; Begin writeln; write(‘Введите количество слагаемых суммы N = ‘); read(n); while k <= n do begin S := S + 1/sqr(2*k + 1); k := k + 1; end; writeln(‘S = ’, S:6:4); readln end. Данные для тестирования 1) Для n = 2 2) Для n = 3
ЧИСЛОВЫЕ РЯДЫ В задачах этой темы необходимо вычислить заданные суммы S. Каждая задача должна решаться в двух вариантах: а) задано число членов суммы N; б) вычисление производить до тех пор, пока очередной член вычисляемой суммы не станет по модулю меньше заданного значения e. Все последующие слагаемые в S входить не должны. При решении задач данной темы для реализации варианта а) должен использоваться оператор цикла с параметром (for), а для реализации варианта б) – оператор цикла с постусловием (repeat) или оператор цикла с предусловием (while) – это определяет конкретный преподаватель. Пример 4.1. Вычислить сумму ряда:
Решение задачи Выберем схему решения поставленной задачи. Данная сумма может быть представлена в виде S=u1-u2+u3-u4+…. Начальное значение суммы – это первое слагаемое u1=1. При вычислении суммы из начального ее значения вычитается значение второго члена последовательности, затем прибавляется значение третьего члена, затем вычитается значение четвертого члена суммы и так далее. То есть при вычислении суммы необходимо учитывать чередование знака слагаемых. Для учета такого чередования надо ввести дополнительную переменную Znak, которая будет принимать значения либо 1, либо –1. Начальное значение знака При вычислении значения суммы надо к предыдущему значению суммы прибавить значение модуля очередного слагаемого, умноженного на знак. При расчете абсолютного значения дроби надо отметить закономерность. Числитель очередного слагаемого равен порядковому номеру члена суммы (обозначим его переменной k). Тогда знаменатель дроби можно рассчитать по формуле (k + 1)2. В варианте а) число членов суммы заранее известно (равно N), и для решения задачи удобно использовать цикл с параметром. В варианте б) значение очередного слагаемого следует запомнить в некоторой переменной (sl), чтобы использовать его при проверке условия прекращения вычислений – модуль последнего слагаемого должен быть меньше заданной величины e. Вычисление суммы в варианте б) организуем с помощью цикла while: пока очередное слагаемое по модулю будет больше e (в алгоритме обозначим её Е), будем выполнять действия в цикле.Чтобы не «потерять» последнее слагаемое, прибавим его к сумме после завершения цикла
 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 711. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||




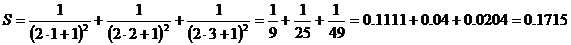

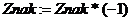 .
.