Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Задание 2. Фильтрация сигналов для демодуляции амплитудно-манипулированных сигналов в гауссовских каналах связи. ⇐ ПредыдущаяСтр 2 из 2
Проделаем задание 2 аналогично заданию 1 с той лишь разницей, что в качестве модулирующего сигнала будет выступать битовая последовательность. В задании использовался модифицированный код из предыдущего задания.
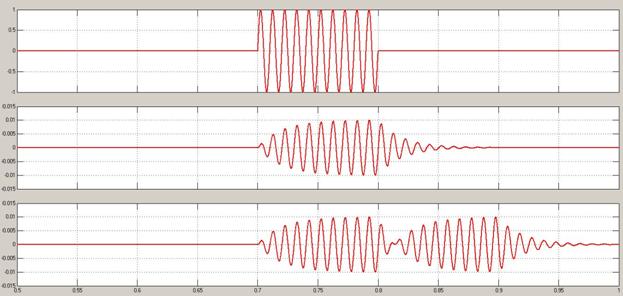
Рис 2. Временное представление модулирующей битовой последовательности, детектируемого сигнала и демодулированного сигналов
Задание 3. Обнаружение детерминированного импульсного сигнала Порядок выполнения работы: 1) Введём известные данные и посчитаем порог Байса для принятия решения
2) Из теории проверки статистических гипотез имеем:
Необходимо проверить соотношение:
Так как помеха, сгенерированная в задании 2, имеет математическое ожидание МО=0 и среднеквадратическое отклонение СКО=1, то:
Листинг программы t=0:0.001:1; %Задаем массив отсчетов времени fc=100; %Задаем частоту несущего сигнала fm=10; %Задаем частоту модулирующего сигнала Uc0=3; %Задаем амплитуду несущего колебания Um0=2; %Задаем амплитуду модулирующего сигнала U0=3; %Задаем постоянную составляющую модулирующего сигнала fi0=pi/3; %Задаем начальную фазу модулирующего колебания m=1; %Задаем коэффициент модуляции Un0=0.3; %Задаем амплитуду белого шума Uc=Uc0*cos(2*pi*fc*t); %Задаем несущее гармоническое колебание Um=U0+Um0*cos(2*pi*fm*t+fi0); %Задаем модулирующий гармонический сигнал Uam=Uc0.*(1+m*Um/max(abs(Um))).*cos(2*pi*fc*t); %Выражение для АМ-сигнала Un=Un0*randn(size(t)); %Генерирует белый шум с МО=0 и СКО=1 Ud=Uam+Un; %Сигнал на входе приемника (аддитивная помеха) U1=Un.^2; U2=Um.^2;  U3=U1+U2; U4=U3'; L=2.71828^(sum(U4)); disp('Отношение правдоподобий') disp(L)
Задача 4. Согласованная фильтрация сигнала. Порядок выполнения работы: 1) Зададим вокне Workspace в среде MatLabпараметры, необходимые для решения задачи:
2) В среде Simulinkсоставим блок-схему, реализующую согласованную фильтрацию сигнала:
Рис 3. Блок-схема согласованной фильтрации сигнала Элементы блок-схемы
Рис. 4. Сигналы
где nnи nd ― порядок числителя и знаменателя передаточной функции; num ― вектор или матрица коэффициентов числителя; den ― вектор коэффициентов знаменателя;
Рис. 5. Сигналы на экране осциллографа из Рис. 6. Список использованной литературы 1. Краткая сводка по Matlab Н.Ю. Золотых 2. Статистические модели и методы обработки сигналов в системах радиосвязи: Учебное пособие / Ш.М.Чабдаров, Р.Р.Файзуллин, А.Ф.Надеев, Р.Х.Рахимов, А.Ю.Феоктистов; Казань: Изд-во Казан, гос. техн. ун-та. 1997. 90с. 3. Файзуллин Р.Р. Комплексный подход к решению задач синтеза и анализа эффективности алгоритмов и мультипроцессорных устройств обработки сигналов мобильных мультисервисных систем. Нелинейный мир, No2, т.9. М.: ЗАО ≪Издательство ≪Радиотехника≫, 2011. стр. 78 – 85. 4. Файзуллин Р.Р., Кадушкин В.В., Воробьев М.С. Полигауссовыйквазиоптимальный алгоритм многопользовательского разрешения сигналов. Нелинейный мир, No10, т.12. М.: ЗАО ≪Издательство ≪Радиотехника≫, 2014. стр. 27 – 31
|
||||||||||||||||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 310. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |


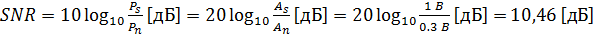 ;
; на фоне АБГШ.
на фоне АБГШ. :
: ;
; ;
; ;
; ;
;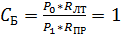 ;
; – гипотеза о том, что в сигнале
– гипотеза о том, что в сигнале 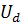 присутствует
присутствует  ;
; – гипотеза о том,в сигнале
– гипотеза о том,в сигнале 
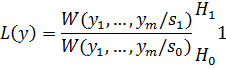


 , следовательно, на основании критерия Байса принимается гипотеза
, следовательно, на основании критерия Байса принимается гипотеза 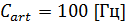 ; Частота синусоидального радиосигнала;
; Частота синусоидального радиосигнала; ; Время начала генерации импульсного сигнала;
; Время начала генерации импульсного сигнала; ; Длительность модулированного импульса;
; Длительность модулированного импульса; ;Масштабированный период радиосигнала (используется при умножении сигналов);
;Масштабированный период радиосигнала (используется при умножении сигналов); ; Циклическая частота синусоидального сигнала;
; Циклическая частота синусоидального сигнала;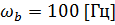 ; Полоса пропускания полосового фильтра;
; Полоса пропускания полосового фильтра;











 задает передаточную функцию в виде отношения полиномов:
задает передаточную функцию в виде отношения полиномов:
 ,
, и
и  — преобразования Лапласа для сигналов
— преобразования Лапласа для сигналов  (входной сигнал) и
(входной сигнал) и  (выходной сигнал), причем:
(выходной сигнал), причем: ;
; ;
;