
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Задание 1. Демодуляция АМ-сигналаСтр 1 из 2Следующая ⇒ Пример №1 Вычислим порог для критерия Котельникова:
Для аналитического обнаружения порога рассмотрим:
Пример №2 Обнаружить цель двумя РЛС (радиолокационная станция) независимо. Априорная вероятность обнаружения цели 1-й станции равна 0,7; 2-й равна 0,8. Нужно определить вероятность обнаружения хотя бы одной станции. Решение: В таких задачах зондирующий импульс детерминированный, случайная помеха отсутствует. Нет необходимости вычислять правдоподобие. Задача сводится к вычислению элементарных событий. Соответственно, вероятность обнаружения: P(A) = 0,7 P(B) = 0,8 P(AB)= P(A)*P(B) = 0,7*0,8 = 0,56 P(C) = P(A+B)=P(A) + P(B) – P(AB)= 0,7+0,8-0,56= 0,94 или
Ответ: вероятность обнаружения одной станции P(C)=0,94. Пример№3: Генерируется два сигнала и расстояние наблюдается на интервале от 0 до t , скважность между двумя импульсами равна Решение:
Решение задачи сводится к отношению ошибочной и полезной областей, область перезагрузки приемника находится в заштрихованной области. При сближении τ1 и τ2 область перегрузки уменьшается, говоря о высокой разрешающей способности приемника. Площадь заштрихованной области равняется s, тогда искомая вероятность есть отношение:  S= T2 s= T2-(T- τ)2
τ= 0,5 c, P(A)=0,75 Оптимальное обнаружение детерминированного сигнала с учётом критических ошибок. На вход приёмника поступает либо случайный процесс в виде шума n(t), либо сумма полезного сигнала и помехи f(t).Рассмотрим две гипотезы:1) Априорные вероятности этих гипотез принимаются равновероятными. Помеха n(t) при стрессовыхГауссовским шумом нулевым и средним и с выборочной дисперсией. В момент времени производится измерение входного процесса и по полученному значению алгоритм принимает решение: был на входе сигнал или не было. Кроме выборочного среднего и выборочной дисперсии иногда используется корреляционный момент. Из-за случайного характера процесса приёма решение в пользу гипотез Пример №4. Три источника сигнала генерируют на базовую станцию свои сигналы. Стоит задача определить вероятность потери связи Решение: Назначим априорные вероятности потерь помехоустойчивости по каждому источнику:
Возникает задача проверки гипотез, которые ведут к событию A. Гипотеза Предположим, что если помехоустойчивость снизилась у одного из источников, то вероятность потери связи равна 0,25. Если только у двоих источников, то будет равняться 0,4. Если же у всех трёх, то это число будет 0,5.
Т.е. связь не будет восстановлена. Ответ: вероятность потери связи Пример №5 Апостериорная вероятность гипотез. По каналу связи передаются сигналы в виде кодовых комбинаций S1 и S0 с априорными вероятностями их передачи P1=0.7 и Р2=0.3. Из-за наличия помех вероятность правильного каждого символа в группе уменьшается до 0.6. Искажения кодовой комбинации происходит независимо друг от друга. Фиксируем прием символов: U=10110 Определить какая команда была передана. S1=11111 P1=0.7 S0=00000 Р2=0.3 P0=0.6 U=10110 H1→S1 H0→S0 Решение: P(A(H1))=0,6*0,4*0,6*0,6*0,4=0,035 P(A(H0))=0,4*0,6*0,4*0,4*0,6=0,023 P(H1(A))= P(H0/A)=0,22 → H1
Пример 6 Имеется множество абонентов – 1000, которые разбросаны по терминалам 2G, 3G, 4G, 5G и разбросаны по трем категориям Home, Corp, VIP
Абоненты взаимодействуют с БС образуя группу событий: А1- БС обрабатывает сигнал абонента группы 2G А2- БС обрабатывает сигнал абонента группы 3G А3- БС обрабатывает сигнал абонента группы 4G А4- БС обрабатывает сигнал абонента группы 5G
1. Какова вероятность обработки базовой станцией сигнала каждого из 4-х стандартов? Возможны всего 4 исхода: Р2G=
2. Какова вероятность обработки базовой станцией сигнала любого из 4-х стандартов, но определенной группы? Возможны всего 3 исхода: PHome= 3. Какова вероятность обработки базовой станцией сигнала VIPабонента стандарта 3G? Таких всего 150 человек. Р(А) = РVIP 3G= !Примечание: если это событие Р(А) вычислять как произведение : Р(АВ) =Р3G*РVIP=0,5*0,36=0,18 ≠ 0,15 следовательно так считать нельзя. Нужно вычислять условные вероятности Р(А/В) Р(А/В) = P(3G/VIP)= P(AB)=P(B)P(A/B)=0,36*0,417=0,15 Условная вероятность выбора сигнала группы VIPиз стандарта 3G P(В/А)= P(AB)=P(А)P(В/А)=0,5*0,3=0,15 4. Базовая станция равновероятно обрабатывает сигнал какого-то абонента. Какова вероятность, что этот сигнал € группе «Home»? У нас выбор сигнала по 4-м стандартам равновероятен, т.е. Р(А1)=Р(А2)=Р(А3)=Р(А4)=0,25 – априорные вероятности P(В)- полная вероятность принадлежности сигнала к группе «Home». >> >> P(B/A1)= >>Р(В)= 5. Предположим, что принятый(обработанный) сигнал € группе Home Какова вероятность того, что он был сгенерирован 3G-абонентом? >>P(A2/В)=
Задание 1. Демодуляция АМ-сигнала Порядок выполнения работы: 1) Зададим временной массив t: 0≤t≤1; 2) Зададим линейные частоты модулирующего 3) Зададим амплитуду несущегосигнала 4) Зададим коэффициент модуляции m: 0<m≤1 (при m>1 наступает перемодуляция(избыточная модуляция)), простые демодуляторы (типа квадратичного детектора) демодулируют такой сигнал с сильными искажениями. 5) Сгенерируем несущий сигнал и модулирующий сигнал, используя входные параметры:
6) Сгенерируем амплитудно-модулированный сигнал
Т.к.
7) Сгенерируем массив случайных величин (соразмерный смассивом t),распределенных по равномерному закону в интервале (0, 1)[белый шум
8) Проведем фильтрацию принимаемого сигнала Операция линейной дискретной фильтрации в общем случае описывается следующим образом:
Максимальное из чисел
Рис 1. Цифровой рекурсивный фильтр Передаточная функция фильтра имеет вид:
В среде MatLab используется функция 9) Зададим параметры фильтра:
И проведем операцию демодуляции принимаемого сигнала.
10) Вычислим отношение сигнал/шум по формуле:
Листинг программы clear t=0:0.001:1; %Задаем массив отсчетов времени fc=100; %Задаем частоту несущего сигнала fm=10; %Задаем частоту модулирующего сигнала Uc0=3; %Задаем амплитуду несущего колебания Um0=2; %Задаем амплитуду модулирующего сигнала U0=3; %Задаем постоянную составляющую модулирующего сигнала Un0=0.1; %Задаем амплитуду белого шума fi0=pi/3; %Задаем начальную фазу модулирующего колебания m=1; %Задаем коэффициент модуляции Uc=Uc0*cos(2*pi*fc*t); %Задаем несущее гармоническое колебание Um=U0+Um0*cos(2*pi*fm*t+fi0); %Задаем модулирующий гармонический сигнал Uam=Uc0.*(1+m*Um/max(abs(Um))).*cos(2*pi*fc*t); %Выражение для АМ-сигнала Un=Un0*randn(size(t)); %Генерирует белый шум с МО=0 и СКО=1 Ud=Uam+Un; %Сигнал на входе приемника (аддитивная помеха) b=[1 1 1]; %Коэффиенты b цифрового фильтра a=1; %Коэффициенты a цифрового фильтра Udmd=filter(b,a,abs(Ud)); subplot(3,2,1) plot(t,Um) grid on xlabel('Время, с') ylabel('Амплитуда, B') title ('Модулирующийсигнал') subplot(3,2,2) plot(t,Uc) grid on xlabel('Время, с') ylabel('Амплитуда, B') title ('Несущееколебание') subplot(3,2,3) plot(t,Uam) grid on xlabel('Время, с') ylabel('Амплитуда, B') title ('АМсигнал') subplot(3,2,4) plot(t,Un) grid on xlabel('Время, с') ylabel('Амплитуда, B') title ('Белыйшум') subplot(3,2,5) plot(t,Ud) grid on xlabel('Время, с') ylabel('Амплитуда, B') title ('Сигнал на входе приемника') subplot(3,2,6) plot(t,Udmd) grid on xlabel('Время, с') ylabel('Амплитуда, B') title ('Отфильтрованный сигнал')
|
|||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 300. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
||||||||||||||||||||||||||||||||||||||||||







 , вводится ограничение: если разница
, вводится ограничение: если разница 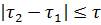 то приемник перегружается и выносит ошибочное решение.
то приемник перегружается и выносит ошибочное решение.  это случайные моменты поступления любых импульсов поступающих независимо от источника 1 и источника 2. Поступления от источников равновероятные. Задача определить вероятность события Р(А) что приемник будет перегружен.
это случайные моменты поступления любых импульсов поступающих независимо от источника 1 и источника 2. Поступления от источников равновероятные. Задача определить вероятность события Р(А) что приемник будет перегружен.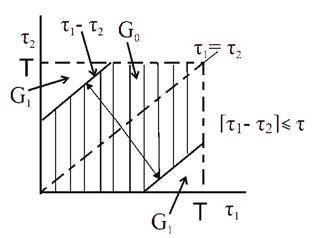 τ1 , τ2 – представляем в виде декартовых координат, а область возможных значений поступлений τ1/τ2 есть T2
τ1 , τ2 – представляем в виде декартовых координат, а область возможных значений поступлений τ1/τ2 есть T2
 сигнал + помеха; 2)
сигнал + помеха; 2)  только помеха.
только помеха.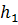 и
и  сопровождаются ошибками двух видов: ошибка первого рода (когда отвергается правильная гипотеза) носит название ложная тревогаF; ошибка второго рода ( когда принимается не правильная гипотеза) носит название пропуск сигналаH.
сопровождаются ошибками двух видов: ошибка первого рода (когда отвергается правильная гипотеза) носит название ложная тревогаF; ошибка второго рода ( когда принимается не правильная гипотеза) носит название пропуск сигналаH.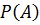 . Каждый источник из-за воздействия помех может потерять связь с базовой станцией.
. Каждый источник из-за воздействия помех может потерять связь с базовой станцией.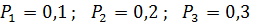
 - помехоустойчивость упала у одного источника. Гипотеза
- помехоустойчивость упала у одного источника. Гипотеза  – помехоустойчивость упала у двух источников. Гипотеза
– помехоустойчивость упала у двух источников. Гипотеза 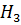 – помехоустойчивость снизилась у всех трёх источников.
– помехоустойчивость снизилась у всех трёх источников.

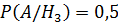

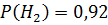
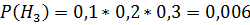


 =
= 

 - Абоненты
- Абоненты =0,1;Р3G=0,5(Р(А)); Р4G=0,15; Р5G=0,25
=0,1;Р3G=0,5(Р(А)); Р4G=0,15; Р5G=0,25
 ; Рcorp= 0,5; РVIP= 0,36(P(B))
; Рcorp= 0,5; РVIP= 0,36(P(B)) =0,15
=0,15 =0,417 – Условная вероятность выбора сигнала стандарта 3Gиз группы VIP
=0,417 – Условная вероятность выбора сигнала стандарта 3Gиз группы VIP =0,3
=0,3 =0,5; P(B/A2)=
=0,5; P(B/A2)= 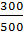 =0,6; P(B/A3)=
=0,6; P(B/A3)= 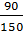 =0,6; P(B/A4)=
=0,6; P(B/A4)=  =0;
=0;  (Аi)Р(В/ Аi)=0,5*0,25+0,6*0,25+0,6*0,25+0*0,25=0,425
(Аi)Р(В/ Аi)=0,5*0,25+0,6*0,25+0,6*0,25+0*0,25=0,425 =
=  = 0,352
= 0,352 и несущего
и несущего 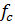 колебаний.
колебаний. . Для модулирующего сигнала зададим амплитуду
. Для модулирующего сигнала зададим амплитуду  , постоянную составляющую
, постоянную составляющую  , и начальную фазу колебаний
, и начальную фазу колебаний  .
. ;
;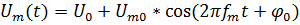 ;
; :
: ;
; ;
; ]. Зададим его амплитуду
]. Зададим его амплитуду  . В канале связи будет создаваться аддитивная помеха, т.е. сигнал на входе приемника будет иметь вид:
. В канале связи будет создаваться аддитивная помеха, т.е. сигнал на входе приемника будет иметь вид: ;
; ;
; — отчёты входного сигнала;
— отчёты входного сигнала; — отчёты выходного сигнала;
— отчёты выходного сигнала; —постоянные коэффициенты;
—постоянные коэффициенты; и
и  называется порядком фильтра.
называется порядком фильтра.
 ;
;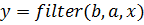 .
. ;
; ;
; ;
;