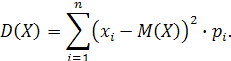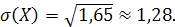Дискретные случайные величины

10) В денежной лотерее выпущено 100 билетов. Разыгрывается четыре выигрыша по 5 тысяч рублей; пять выигрышей по 4 тысячи рублей и одиннадцать выигрышей по 1 тысячи рублей.

а) Составить ряд распределения случайной величины X – размер выигрыша по одному купленному билету.

б) Найти математическое ожидание, дисперсию и среднее квадратическое отклонение случайной величины.

в) Записать функцию распределения и построить ее график.

Решение

а) Случайная величина X – размер выигрыша по одному купленному билету.

Возможные значения случайной величины:

0; 1; 4; 5.

Вероятность выиграть 5 тысяч рублей по одному билету:

Аналогично определяются вероятности остальных значений случайной величины.

Ряд распределения имеет вид:

б) Найдем числовые характеристики случайной величины.

Ответ:

Теоремы сложения и умножения вероятностей

Варианты 1-10 (N – номер варианта)

В урне N белых и (25 – N) черных шаров. Из урны последовательно достают два шара. Найти вероятность того, что:

1) шары будут разных цветов, если шары возвращают в урну;

2) шары будут одинакового цвета, если шары не возвращают в урну;

3) хотя бы один шар будет белым, если шары не возвращают в урну.

Варианты 11-20 (N – номер варианта)

В урне (N – 6) белых и (31 – N) черных шаров. Из урны последовательно достают все шары. Найти вероятность того, что

1) третьим по порядку будет вынут белый шар;

2) из первых трех шаров хотя бы один будет белым шаром.

Варианты 21-30 (N – номер варианта)

В урне (N – 16) белых и 5 черных шаров и (36 – N) красных шаров. Три из них вынимаются наугад. Найти вероятность того, что по крайней мере два из них будут разноцветными при условии: а) шары возвращаются в урну; б) шары не возвращаются в урну.

Формула полной вероятности. Формула Байеса

Варианты 1-10 (N – номер варианта)

Имеются три одинаковые с виду урны. В первой N белых шаров и
(25 – N) черных шаров; во второй урне (20 – N) белых и (N + 5) черных; в третьей только белые шары. Из наугад выбранной урны достают один шар. Какова вероятность, что этот шар белый?

Варианты 11-20 (N – номер варианта)

Имеются две урны: в первой (N – 5) белых шаров и (30 – N) черных шаров; во второй урне (21 – N) белых и (N + 4) черных. Из первой урны во вторую перекладывают, не глядя, один шар. После этого из второй урны достают один шар. Найти вероятность того, что этот шар будет белым.

Варианты 21-30 (N – номер варианта)

Имеются три урны: в первой (N – 15) белых шаров и (35 – N) черных шаров; во второй урне (40 – N) белых и (N – 20) черных; в третьей – N белых шаров (черных нет). Из наугад выбранной урны достали один шар. Этот шар оказался белым. Найти вероятность того, что шар достали из первой урны.

Формула Бернулли

Варианты 1-10 (N – номер варианта)

В семье 6 детей. Вероятность рождения мальчика равна 0,51. Найти вероятность того, что среди этих детей:

N = 1) один мальчик;

N = 2) более одного мальчика;

N = 3) два мальчика;

N = 4) более двух мальчиков;

N = 5) не более двух мальчиков;

N = 6) три мальчика;

N = 7) более трех мальчиков;

N = 8) не более трех мальчиков;

N = 9) четыре мальчика;

N = 10) не более четырех мальчиков.

Варианты 11-20 (N – номер варианта)

Отрезок АВ разделен точкой С в отношении 3:1. На этот отрезок наудачу брошено шесть точек. Предполагается, что вероятность попадания точки на отрезок пропорциональна длине отрезка и не зависит от его расположения. Найти вероятность того, что:

N = 11) одна точка окажется левее точки С;

N = 12) более одной точки окажется левее точки С;

N = 13) две точки окажется левее точки С;

N = 14) более двух точек окажется левее точки С;

N = 15) не более двух точек окажется левее точки С;

N = 16) три точки окажется левее точки С;

N = 17) более трех точек окажется левее точки С;

N = 18) не более трех точек окажется левее точки С;

N = 19) четыре точки окажется левее точки С;

N = 20) не более четырех точек окажется левее точки С.

Варианты 21-30 (N – номер варианта)

Монету бросают 6 раз. Найти вероятность того, что «герб» выпадет:

N = 21) один раз;

N = 22) более одного раза;

N = 23) два раза;

N = 24) более двух раз;

N = 25) не более двух раз;

N = 26) три раза;

N = 27) более трех раз;

N = 28) не более трех раз;

N = 29) четыре раза;

N = 30) не более четырех раз.