
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Задача 2. Задача об оптимальной диетеИмеется n видов продуктов питания, в которых содержится m типов питательных веществ (белки, жиры, углеводы). В одной весовой единице продукта i-го типа (i Требуется определить оптимальный состав рациона продуктов, такой, чтобы каждое питательное вещество содержалось в нем в необходимом количестве, обеспечивающем суточную потребность человека, и при этом суммарная калорийность рациона была минимальной. Ведем в рассмотрение следующие переменные: х – весовое количество продукта питания i-го типа в суточном рационе. Тогда в общем случае математическая постановка задачи об оптимальной диете может быть сформулирована следующим образом: где множество допустимых альтернатив ∆ß формируется следующей системой ограничений типа неравенств: x1, x2, …, xn ≥ 0 (6) Для решения задачи об оптимальной диете с помощью программы MS Excel необходимо задать конкретные значения параметрам исходной задачи. Для определенности предположим, что в качестве исходных типов продуктов рассматриваются: хлеб, мясо, сыр, бананы, огурцы, помидоры, виноград (n = 7), а в качестве питательных веществ рассматриваются белки, жиры, углеводы (m = 3).  Калорийность одной весовой единицы каждого из продуктов следующая: с1 = 2060, с2 = 2430, с3 = 3600, с4 = 890, с5 = 140, с6 = 230, с7 = 650. Содержание питательных веществ в каждом из продуктов может быть задано в форме нижеприведенной таблицы. Минимальная суточная потребность в питательных веществах следующая: в белках b1 = 100, в жирах b2 = 70, в углеводах b3 = 400. Для решения данной задачи c помощью программы MS Excel создадим новую книгу с именем Линейное программирование и изменим имя ее второго рабочего листа наЗадача о диете. Таблица – Содержание питательных веществ в продуктах питания
Этап. Создание математической модели задачи Составим математическую модель процесса по описанию задачи: 2060Х1+2430Х2+3600Х3+890Х4+140X5+230X6+650X7=Fmin – целевая функция (суммарная калорийность продуктов). {61Х1+220Х2+230Х3+15Х4+8X5+11X6+2X7 >= 100 {12Х1+172Х2+290Х3+Х4 +X5+2X6+6X7 >=70 – ограничения модели {420Х1+212Х4 +26X5+38X6+155X7 >=400 x1,x2,…,xn ≥ 0, где n=7 – граничные условия Этап. Создание формы Для решения поставленной задачи выполним следующие подготовительные действия: 1. Внесем необходимые надписи в ячейки A1:I1, A2:A7, B4, I4, J4. 2. В ячейки ВЗ:НЗвведем значения коэффициентов целевой функции: с1 = 2060, c2 = 2430, c3 = 3600, c4 = 890, c5 = 140, c6 = 230, c7= 650. 3. В ячейку I2 введем формулу: =СУММПРОИЗВ(B2:Н2;B3:H3), которая представляет целевую функцию (4). 4. В ячейки В5:Н7введем значения коэффициентов ограничений, взятых из таблицы.
Рисунок 6.4 – Исходные данные для решения задачи об оптимальной диете 5. В ячейки J5:J7введем значения правых частей ограничений, соответствующих минимальной суточной потребности в питательных веществах: в белках b1=100, жирах b2= 70 и углеводах b3= 400. 6. В ячейку I5введем формулу: =СУММПРОИЗВ($B$2:$H$2;В5:Н5), которая представляет левую часть первого ограничения (5). 7. Скопируем формулу, введенную в ячейку I5,в ячейки I6 и I7. 8. Внешний вид рабочего листа MSOfficeExcel с исходными данными для решения задачи об оптимальном рационе питания имеет следующий вид (pиc. 6.4). Следует напомнить, что для отображения формул в ячейках рабочего листа необходимо выполнить операцию главного меню: Сервис | Параметры и в открывшемся диалоговом окне на вкладке Видотметить флажком строку выбора Формулыв группе Параметрыокна.
|
||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 604. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 {1, 2, ..., n}) содержится аi единиц питательного вещества j-го вида (j
{1, 2, ..., n}) содержится аi единиц питательного вещества j-го вида (j  (4)
(4)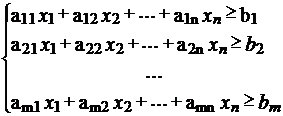 (5)
(5)