
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Лекция 2 Решение систем линейных уравнений ⇐ ПредыдущаяСтр 2 из 2 Системой линейных алгебраических уравнений (СЛАУ) называется система вида
Решением системы (1) называется такая совокупность n чисел Решить систему означает найти все ее решения или доказать, что ни одного решения нет. СЛАУ называется совместной, если она имеет хотя бы одно решение, и несовместной, если она решений не имеет. Если совместная система имеет только одно решение, то она называется определенной, и неопределенной, если она имеет более чем одно решение. Две системы уравнений называются равносильными или эквивалентными, если они имеют одно и то же множество решений. В частности, две несовместные системы считаются эквивалентными. Основной матрицей СЛАУ (1) называется матрица А размера
Матрицей неизвестных СЛАУ (1) называется матрица-столбец Х, элементами которой являются неизвестные системы (1):
Матрицей свободных членов СЛАУ (1) называется матрица-столбец В, элементами которой являются свободные члены данной СЛАУ:
С учетом введенных понятий СЛАУ (1) можно записать в матричном виде
Рассмотрим в общем виде систему уравнений АХ = В с невырожденной квадратной матрицей А. В этом случае существует обратная матрица А-1. Домножим слева обе части на А-1. Получим А-1АХ = А-1В. Отсюда ЕХ = А-1В и Х = А-1В. Последнее равенство представляет собой матричную формулу для нахождения решения таких систем уравнений. Использование этой формулы получило название метода обратной матрицы  Правило и формулы Крамера Рассмотрим систему
Учитывая равенство
Таким образом, после перемножения матриц получаем:
Заметим, что сумма
по элементам первого столбца, который получается из определителя Таким образом, можно сделать вывод, что Аналогично: Следовательно, нами найдено решение заданной системы по равенствам
известным, как формулы Крамера. Для нахождения решения СЛАУ, последние равенства можно записать в общем виде следующим образом:
Согласно этим формулам, имеем правило Крамера для решения СЛАУ: по матрице системы если
Лекция 3 Комплексные числа
Комплексным числом называется число вида z = x +iy, где x и y – действительные числа, i – мнимая единица, то есть число, квадрат которого равен (минус) –1, x – действительная часть, y – мнимая часть. Если x = 0, то число z = iy чисто мнимое. Запись z = x + iy – алгебраическая форма записи числа. Два комплексных числа z1 = x1+iy1и z2=x2+iy2называются равными (z1=z2) тогда и только тогда, когда равны их действительные части и равны их мнимые части: x1=x2, y1=y2. Понятия «больше» и «меньше» для комплексных чисел не вводятся. Два комплексных числа вида z = x + iy и z = x – iy называются комплексно-сопряженными. Всякое комплексное число z = x + iy можно изобразить точкой М(x,y) на плоскости Оxy и, наоборот, каждую точку М(x,y) координатной плоскости можно рассматривать как образ комплексного числа z = x + iy. Плоскость, на которой изображаются комплексные числа, называется комплексной плоскостью. Комплексное число z = x + iy можно также изобразить в виде радиус-вектора r = ОМ. Длина вектора r = │ОМ│ называется модулем комплексного числа. Угол φ, образованный вектором OM с положительным направлением оси Ox называется аргументом комплексного числа: φ = Arg z. Аргумент комплексного числа величина многозначная Arg z = arg z +2πk, где arg z – главное значение аргумента, – π < arg z <+ π (или [0, 2π)). Угол φ таков, что cos φ = x/r; sin φ = y/ r.
Если x и y - декартовы координаты точки плоскости, то, перейдя на плоскости к полярным координатам (r, φ) и воспользовавшись связью x = rcos φ, y = rsin φ получим тригонометрическую форму записи комплексного числа: z = r (cos φ + isin φ) .
Используя формулу Эйлера еiφ= cos φ+isin φ получим показательную формузаписи комплексного числа: Z= z еiφ Cуммой комплексных чисел z1 и z2 называется комплексное число z вида z = (x1 + x2; y1 + y2). Произведением комплексных чисел z1 и z2 называется комплексное число z = (x1x2 – y1y2; x1y2 + x2y1). Разностью комплексных чисел z1 и z2 называется комплексное число z такое, что z2 + z = z1, откуда находим z = z1 – z2 = (x1 – x2, y1 – y2).
Лекция 4 Дробно-рациональные функции
Дробно-рациональные функции комплексного переменного в различных формах широко используют в ТАУ для представления передаточных функций и решения задач синтеза и анализа САУ. Дробно-рациональная функция некоторого действительного или комплексного переменного
где Полиномы дробно-рациональной функции могут быть представлены в виде произведения биномов (разложение многочлена на сомножители), тогда функция может быть представлена в форме Боде
где Корни уравнения
Корни характеристического уравнения
Полюсы и нули могут быть действительными и комплексно-сопряженными числами. Таким образом, задача представления функции в форме Боде сводится к поиску корней уравнений, образованных полиномами числителя и знаменателя. Их принято располагать на плоскости комплексной переменной
Рис. 1
Мнимая ось делит плоскость Пример Представьте дробно-рациональную функцию
в форме Боде и покажите расположение полюсов и нулей дробно-рациональной функции на комплексной плоскости. Решение Найдем корни уравнения
Получаем два комплексно-сопряженных корня (нуля)
Найдем полюсы
Получаем три полюса
Покажем расположение нулей и полюсов на комплексной плоскости (см. рис. 2).
Рис. 2 Дробно-рациональную функцию (1) часто представляют в виде суммы простейших дробей (форма Хэвисайта)
где
Такое представление дробно-рациональной функции возможно, если полюсы Функция, которая имеет один нулевой полюс, может быть представлена в следующем виде:
В этом случае вместо формул (3), (4) применяют выражение
где
Следовательно, представление дробно-рациональной функции в форме Хэвисайта сводится к нахождению полюсов дробно-рациональной функции и рациональному использованию формул разложения. Рассмотрим ряд примеров получения формы Боде. Пример Представьте дробно-рациональную функцию
в форме Хэвисайта, используя формулы разложения (3), (4). Решение Уравнение полинома числителя имеет вид
Характеристическое уравнение имеет вид
Найдем корни характеристического уравнения
Определим производную от полинома знаменателя
Определим коэффициенты разложения соответствующие по номеру полюсам
Тогда форма Хэвисайта имеет вид
Пример Представьте дробно-рациональную функцию
в форме Хэвисайта, используя формулы разложения (5), (6). Решение Представим
Тогда
Ненулевые полюсы имеют вид
Производная от
Определим коэффициенты разложения
Тогда форма Хэвисайта имеет вид
Импульсные функции
Реальные сигналы (переменные и воздействия), встречающиеся в системах управления, обычно представляют с помощью некоторых идеализаций – импульсных функций. Чаще всего используют ступенчатую единичную функцию (функцию Хэвисайта) и дельта-функцию (функцию Дирака), которые описываются следующим образом:
Графики этих функций показаны на рис. 3.
Рис. 3 Для единичной и дельта-функции справедливо
Таким образом, дельта-функция представляет собой мгновенный импульс, равный бесконечности в нулевой момент времени и нулю в другие моменты, площадь которого постоянна и равна единице. Поэтому иногда
Контрольные вопросы и задачи 1. Как определить порядок дробно-рациональной функции? 2. Поясните процедуру преобразования функции к форме Боде. 3. Какие полюсы дробно-рациональной функции называют простыми? 4. В чем состоит идеализация представления реального сигнала единичной ступенчатой функцией? 5. Представьте дробно-рациональную функцию
в форме Боде. Ответ:
6. Представьте дробно-рациональную функцию
в форме Хэвисайта. Ответ:
7. Представьте дробно-рациональную функцию
в форме Хэвисайта. Ответ:
Лекция 5 Преобразование Фурье
Соотношение
называют прямым преобразованием Фурье. Функция угловой частоты
где Спектры в теории автоматического управления представляют графически, изображая отдельно их действительную и мнимую части:
На рис. 1 представлено типичное изображение спектра непериодического сигнала.
Рис. 1 Отметим следующие особенности спектра непериодической функции 1. Спектр непериодической функции времени непрерывен; 2. Область допустимых значений аргумента спектра
3. Действительная часть спектра – четная функция частоты, мнимая часть спектра – нечетная функция, что позволяет использовать одну половину спектра
Преобразование Фурье обратимо, то есть, зная Фурье-изображение, можно определить исходную функцию – оригинал. Соотношение обратного преобразования Фурье имеет следующий вид:
или в сокращенной записи · функция однозначна, содержит конечное число максимумов, минимумов и разрывов; · функция абсолютно интегрируема, то есть
Обратное преобразование Фурье возможно только в том случае, если все полюсы Рассмотрим примеры определения спектра временных функций. Пример: Найдем частотный спектр дельта-функции.
так как при
а при
В итоге,
Рис. 2 Пример: Найдем частотный спектр единичной ступенчатой функции. Для этой функции не выполняется требование абсолютной интегрируемости, так как
Поэтому
Преобразование Лапласа
Соотношение
называют прямым преобразованием Лапласа. Комплексная переменная Преобразование Лапласа обратимо, то есть, зная изображение по Лапласу, можно определить оригинал, используя соотношение обратного преобразования
или Отметим, что преобразование Лапласа изображает исходную функцию лишь при Получим изображения по Лапласу для импульсных функций.
так как
На практике для выполнения прямого и обратного преобразований Лапласа используются таблицы преобразований, фрагмент которой показан в табл. 1. Таблица 1.
Таблицы преобразования Лапласа могут быть использованы для определения Фурье-изображений таких абсолютно интегрируемых функций, которые равны 0 при
если Рассмотрим формулировки основных теорем преобразования Лапласа, которые широко используются в ТАУ. 1. Теорема линейности. Любое линейное соотношение между функциями времени справедливо и для изображений по Лапласу этих функций;
2. Теорема о дифференцировании оригинала. Если где Дифференцирование 3. Теорема об интегрировании оригинала.
Замечание В области изображений по Лапласу сложные операции дифференцирования и интегрирования сводятся к операциям умножения и деления на Для нахождения оригинала функции по ее изображению используют обратное преобразование Лапласа. Функцию изображения необходимо представить в форме Хэвисайта, воспользовавшись необходимой формулой разложения дробно-рациональной функции. Полученную сумму простейших дробей подвергают обратному преобразованию Лапласа. Для этого можно воспользоваться таблицами преобразования Лапласа, которые определяют изображения многих временных функций. Фрагмент таблицы преобразования Лапласа приведен в табл. 1. В тех случаях, когда имеются комплексно-сопряженные полюсы изображения, необходимо преобразовать соответствующие простейшие дроби к виду, удобному для использования таблицы преобразования Лапласа. Пример Определим оригинал
Используем разложение Хэвисайта для дробно-рациональной функции с одним нулевым полюсом. Тогда
Коэффициенты разложения имеют вид
Изображение в форме Хэвисайта имеет вид
Используем теорему о линейности и таблицу преобразований к каждому слагаемому, в результате получаем
График функции оригинала имеет вид, показанный на рис. 3.
Рис. 3 Кратко поясним алгоритм решения дифференциальных уравнений операторным методом на примере решения дифференциального уравнения 2 порядка в общем виде
где Применим теорему о дифференцировании для нахождения изображений производных
Пусть
Получим операторное уравнение, используя теорему линейности
Решаем уравнение относительно
Найдем
где Особо следует обратить внимание на получение изображения производной ступенчатой единичной функции
Если использовать
то получается ошибочное решение, поэтому следует использовать называемые "левые" начальные условия
Справедливость этого можно легко проверить подстановкой решения в исходное дифференциальное уравнение.
Контрольные вопросы и задачи 1. Какие ограничения накладываются на прямое и обратное преобразование Фурье? 2. Как с помощью таблиц преобразования Лапласа получить частотный спектр реального сигнала – непериодической функции времени? 3. Если изображение по Лапласу имеет вид дробно-рациональной функции, в какой форме ее удобнее представлять для получения оригинала, в форме Боде или в форме Хэвисайта? 4. Определите оригинал следующего изображения по Лапласу
Ответ:
5. Определите оригинал следующего изображения по Лапласу
Ответ:
6. Найдите
где Ответ:
7. Найдите
где Ответ:
Лекция 6 Понятие линейного динамического звена
САУ удобно представлять для анализа и при синтезе в виде взаимосвязанной совокупности отдельных элементов – динамических звеньев. Под динамическим звеном понимают в общем случае абстрактное устройство, имеющее вход и выход, и для которого задано уравнение, связывающее сигналы на входе и выходе, как это показано на рис. 1.
Рис. 1 Подробное изучение свойств реальных объектов управления и систем автоматического управления приводит к описанию динамических звеньев в виде нелинейных дифференциальных уравнений. Но во многих случаях их можно линеаризовать, то есть заменить нелинейные уравнения линейными, приближенно описывающими процессы в системах. Тем самым осуществляется декомпозиция задач анализа и синтеза систем, то есть первоначально используют линейное представление, а затем осуществляют учет вносимых нелинейностями особенностей. Такому подходу способствует то, что, в большинстве случаев, нормально функционирующая система работает в режиме малых отклонений, при которых нелинейности не проявляются. В дальнейшем мы будем рассматривать преимущественно аппарат изучения линейных систем, а особенности систем других классов: нелинейных, импульсных, цифровых и стохастических, будут излагаться позднее в других учебных дисциплинах. Если уравнение, связывающее сигналы Уравнение линейного динамического звена имеет следующий общий вид:
где Использовать такое описание динамического звена в задачах анализа и синтеза систем и объектов управления не рационально, поэтому существуют и иные формы описания и представления динамических звеньев и систем в целом.
Передаточная функция
Подвергнем уравнение (1) преобразованию Лапласа, считая начальные условия нулевыми и заменяя оригиналы сигналов их изображениями по Лапласу
Используя теоремы преобразования Лапласа линейности и дифференцирования, получим операторное уравнение, связывающие изображения входного и выходного сигналов
Преобразуем уравнение (2) к следующему виду
Получим из (3) отношение изображений выходного и входного сигналов
Отношение (4) не зависит от изображений сигналов, определяется только параметрами самого динамического звена ( Отношение изображений выходного и входного сигналов называют передаточной функцией динамического звена
Уравнение вида
называют характеристическим уравнением динамического звена, так как знаменатель передаточной функции – это характеристический полином дифференциального уравнения, описывающего динамическое звено.
Пример
Определим передаточную функцию динамического звена по его принципиальной электрической схеме
Рис. 2 Решение: По второму закону Кирхгоффа запишем уравнения описывающие схему
С учетом того, что
получаем
Получим операторные уравнения
Из второго уравнения выразим значение изображения тока
Подставим полученное выражение в первое уравнение системы
В итоге получаем искомую передаточную функцию
Структурная схема
Графически передаточные функции динамического звена представляют в следующем виде:
Рис. 3 Если известно изображение входного сигнала и передаточная функция динамического звена, всегда можно найти изображение выходного сигнала при нулевых начальных условиях
В общем случае САУ состоит из множества динамических звеньев, сигналы с выходов звеньев могут суммироваться или вычитаться, суммироваться с внешними для САУ сигналами. Суммирование и вычитание изображений сигналов могут быть представлено графически с помощью суммирующих звеньев: 1.
2.
Показанная выше неоднозначность графического представления вычитания изображений на суммирующем элементе связана с различием в стандартах разных стран. Используя графическое представление передаточных функций звеньев и суммирующие звенья, можно в графической форме представить операторные уравнения, описывающие САУ. Такое графическое представление операторных уравнений в ТАУ называют структурной схемой. Пример По математической модели объекта управления в форме системы дифференциальных уравнений определить структурную схему объекта.
Решение: Получим систему операторных уравнений, подвергнув исходную систему дифференциальных уравнений преобразованию Лапласа и заменив оригиналы изображениями,
Из первого уравнения системы операторных уравнений, которое описывает динамическое звено объекта управления, после преобразований получим
Тогда передаточная функция этого звена имеет вид
а выражение
Из второго уравнения системы операторных уравнений, которое описывает динамическое звено объекта управления, после преобразований получим, вводя обозначение,
Тогда передаточная функция этого звена имеет вид
а выражение
Соединим все фрагменты структурной схемы объекта управления, объединяя одноименные сигналы, либо разветвляя их с помощью точек ветвления , показанных на схеме. В результате получим
Временные характеристики динамического звена
Временной или импульсной характеристикой динамического звена называют реакцию звена на
Рис. 4 Выясним, что представляет собой временная характеристика, то есть почему ее называют характеристикой динамического звена? Для этого рассмотрим динамическое звено с передаточной функцией
Рис. 5 В этом случае, в соответствии с (5), имеем
Таким образом
Получаем, что передаточная функция звена – это изображение по Лапласу импульсной характеристики динамического звена. В свою очередь, импульсная характеристика может быть определена по передаточной функции
при использовании разложения в форму Хэвисайта и обратное преобразование Лапласа. Знание импульсной характеристики позволяет определить реакцию динамического звена на сигнал любой формы. Для динамического звена с передаточной функцией
а если легко получить
Переходной характеристикой или переходной функцией динамического звена называют реакцию динамического звена на
Рис. 6 Для анализа переходной характеристики рассмотрим динамическое звено с передаточной функцией
Рис. 7 В этом случае, в соответствии с (5), имеем
По теореме об интегрировании оригинала имеем
Переходная функция является интегралом по времени от импульсной характеристике и наоборот
Переходная характеристика динамического звена может быть определена по передаточной функции
Контрольные вопросы и задачи 1. Что такое линейное динамическое звено? 2. Как определить передаточную функцию линейного динамического звена? 3. Перечислите основные элементы структурных схем систем управления. 4. Как определить по передаточной функции динамического звена его временные характеристики: импульсную и переходную? 5. Как по переходной характеристике определить импульсную характеристику динамического звена? 6. Определите передаточную функцию динамического звена по его принципиальной электрической схеме
Ответ:
7. Определите передаточную функцию динамического звена по его принципиальной электрической схеме
Ответ:
8. По математической модели объекта управления в форме системы дифференциальных уравнений определить структурную схему объекта.
Ответ:
Лекция 7 Частотные характеристики динамического звена Частотной характеристикой динамического звена называют функцию комплексного аргумента
Получим связь частотной характеристики с известными понятиями. Для этого рассмотрим динамическое звено с передаточной функцией
Получим отношение спектров
Таким образом, частотную характеристику динамического звена можно определить как отношение спектра (преобразования Фурье) выходного сигнала к спектру входного сигнала. Знание частотной характеристики звена позволяет определить выходной спектр по входному
Рассмотрим динамическое звено –
Рис. 1 Получим спектр выходного сигнала – импульсной характеристики
Тогда имеем
то есть преобразование Фурье от импульсной характеристики равно частотной характеристике динамического звена. Частотная функция характеристика как функция комплексного аргумента может быть представлена в следующем виде –
где
Амплитуда, фаза, действительная и мнимая части частотной характеристики являются функциями частоты, поэтому частотная характеристика используется и графически представляется в виде амплитудно-фазовой, действительной, мнимой, амплитудной и фазовой частотных характеристик. В теории автоматического управления рассматривают и используют следующие частотные характеристики динамических звеньев: 1. Амплитудно-частотная характеристика (АЧХ) –
2. Фазочастотная характеристика (ФЧХ) –
3. Вещественная частотная характеристика (ВЧХ) –
4. Мнимая частотная характеристика (МЧХ) –
5. Амплитудно-фазовая частотная характеристика (АФЧХ), которая определяется как годограф (след движения конца) вектора На рис. 2 покажем частотные характеристики некоторого динамического звена.
Рис. 2 Для выяснения физического смысла частотной характеристики рассмотрим динамическое звено с передаточной функцией
Рис. 3 Вспомним, что решение линейного дифференциального уравнения динамического звена, в рамках классического метода, состоит из двух составляющих – свободной и установившейся. Установившаяся составляющая в случае гармонической функции времени, стоящей в правой части уравнения, так же является гармонической функцией времени. Поэтом установившийся сигнал на выходе динамического звена можно описать следующим выражением
Сигнал на выходе звена определим с помощью теоремы об умножении изображений
В результате получаем
Для перехода к установившемуся режиму полагаем
Но, с другой стороны, имеем по определению прямого преобразования Фурье
Поэтому
Отсюда следует простой алгоритм экспериментального определения частотной характеристики линейного динамического звена, объекта или системы управления для конкретной частоты 1. Подать на вход объекта синусоидальный сигнал частоты 2. Дождаться затухания свободной составляющей переходного процесса. 3. Измерить амплитуду выходного сигнала и сдвиг его по фазе относительно входного сигнала. 4. Отношение амплитуды выходного установившегося сигнала к амплитуде входного сигнала определит модуль частотной характеристики при частоте 5. Сдвиг фазы выходного сигнала относительно входного сигнала определит угол (аргумент) частотной характеристики при частоте Применяя данный алгоритм для частот от нуля до бесконечности, можно экспериментальным путем определить частотную характеристику конкретного устройства. |
||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 214. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
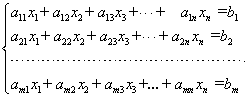 (1)
(1) , при подстановке которых каждое уравнение системы обращается в верное равенство.
, при подстановке которых каждое уравнение системы обращается в верное равенство.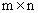 , элементами которой являются коэффициенты при неизвестных данной системы, то есть
, элементами которой являются коэффициенты при неизвестных данной системы, то есть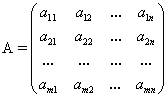 .
. .
. .
. или
или . (2)
. (2) линейных уравнений с
линейных уравнений с 
 , или в развернутом виде
, или в развернутом виде .
. или
или .
. есть разложение определителя
есть разложение определителя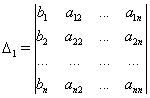
 путем замены первого столбца коэффициентов столбцом из свободных членов.
путем замены первого столбца коэффициентов столбцом из свободных членов.
 , где
, где  получен из
получен из  .
. ,
, 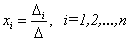 .
. вычисляется определитель системы
вычисляется определитель системы  ;
; , то в матрице системы каждый столбец последовательно заменяется столбцом свободных членов и вычисляются определители
, то в матрице системы каждый столбец последовательно заменяется столбцом свободных членов и вычисляются определители  получаемых при этом матриц; решение системы находится по формулам Крамера.
получаемых при этом матриц; решение системы находится по формулам Крамера.

 Частным комплексных чисел z1 и z2 называется комплексное число z такое, что
Частным комплексных чисел z1 и z2 называется комплексное число z такое, что  .
. имеет следующий вид:
имеет следующий вид:
 - полиномы числителя и знаменателя,
- полиномы числителя и знаменателя, 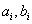 - действительные числа,
- действительные числа,  - порядок числителя,
- порядок числителя,  - порядок знаменателя (всей дробно-рациональной функции функции),
- порядок знаменателя (всей дробно-рациональной функции функции),  - для функций используемых в ТАУ.
- для функций используемых в ТАУ.
 - корни уравнения
- корни уравнения  ,
,  - корни характеристического уравнения
- корни характеристического уравнения  .
. , так как
, так как .
. .
. . На рис. 1 показано расположение полюсов и нулей некоторой дробно-рациональной функции.
. На рис. 1 показано расположение полюсов и нулей некоторой дробно-рациональной функции.
 – 2). Рассмотрим пример получения формы Боде.
– 2). Рассмотрим пример получения формы Боде.
 .
. ,
, 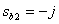 .
.
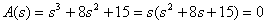 .
.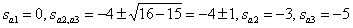 .
.
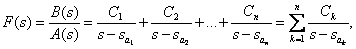
 - корни характеристического уравнения
- корни характеристического уравнения 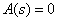 ,
,  - коэффициенты разложения, которые находят по следующей функции:
- коэффициенты разложения, которые находят по следующей функции:
 .
.

 - ненулевые полюсы
- ненулевые полюсы  ,
,

 .
. .
. ,
,  .
. .
. ,
,  .
. .
.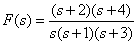

 ,
, .
. ,
,  .
.
 .
. ,
,  ,
,  .
. .
.

 .
.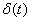 называют единичным импульсом.
называют единичным импульсом.
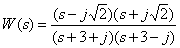 .
.
 .
.
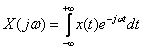
 –
–  называется Фурье-изображением или частотным спектром функции
называется Фурье-изображением или частотным спектром функции  . Спектр характеризует соотношение амплитуд и фаз бесконечного множества бесконечно малых синусоидальных компонент, составляющих в сумме непериодический сигнал
. Спектр характеризует соотношение амплитуд и фаз бесконечного множества бесконечно малых синусоидальных компонент, составляющих в сумме непериодический сигнал 
 - символ прямого преобразования Фурье.
- символ прямого преобразования Фурье.


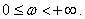

 , где
, где  - символ обратного преобразования Фурье. Заметим, что временная функция имеет преобразование Фурье тогда и только тогда, когда:
- символ обратного преобразования Фурье. Заметим, что временная функция имеет преобразование Фурье тогда и только тогда, когда:
 ,
,
 ,
,
 и
и

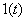 Фурье-изображения не имеет.
Фурье-изображения не имеет.
 называется оператором Лапласа, где
называется оператором Лапласа, где  - некоторое положительное постоянное число. Функция комплексной переменной
- некоторое положительное постоянное число. Функция комплексной переменной  называется изображением сигнала
называется изображением сигнала  , где
, где  - символ прямого преобразования Лапласа.
- символ прямого преобразования Лапласа.
 , где
, где  - символ обратного преобразования Лапласа.
- символ обратного преобразования Лапласа. , а поведение исходной функции при
, а поведение исходной функции при  никак не сказывается на изображении. Класс функций, преобразуемых по Лапласу, значительно шире класса функций, преобразуемых по Фурье. Практически любые функции времени в ТАУ имеют преобразование Лапласа.
никак не сказывается на изображении. Класс функций, преобразуемых по Лапласу, значительно шире класса функций, преобразуемых по Фурье. Практически любые функции времени в ТАУ имеют преобразование Лапласа.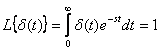 ,
, при
при  .
.




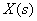



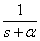
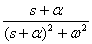
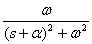
 . Для получения Фурье-изображений в этом случае достаточно положить в изображении по Лапласу
. Для получения Фурье-изображений в этом случае достаточно положить в изображении по Лапласу  . В общем виде это выглядит как
. В общем виде это выглядит как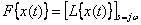 ,
, при
при  ;
; и
и  ,
, - начальное значение оригинала.
- начальное значение оригинала. .
. ;
; .
. .
. .
. .
. .
.
 ,
, ,
,  ,
,  .
. ,
,  .
. , тогда
, тогда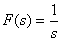 .
. ,
, .
. .
. ,
, ,
,  .
.
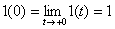 ,
,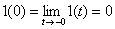 .
.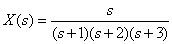 .
.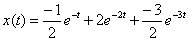 .
.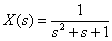 .
. .
. ,
, .
.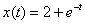 .
. ,
,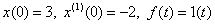 .
.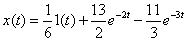 .
.
 и
и  , линейно, то говорят о линейном динамическом звене
, линейно, то говорят о линейном динамическом звене
 - постоянные коэффициенты,
- постоянные коэффициенты,  .
.

 ), имеет вид дробно-рациональной функции.
), имеет вид дробно-рациональной функции. .
. ,
,

 ,
,

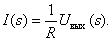
 .
. .
.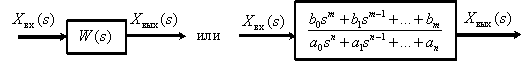
 .(5)
.(5)





 .
. ,
, описывает суммирующее звено
описывает суммирующее звено 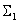 . Таким образом, получены два фрагмента структурной схемы
. Таким образом, получены два фрагмента структурной схемы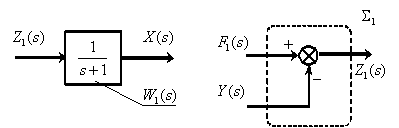
 .
. ,
,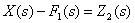 описывает суммирующее звено
описывает суммирующее звено  . Таким образом, получены еще два фрагмента структурной схемы
. Таким образом, получены еще два фрагмента структурной схемы
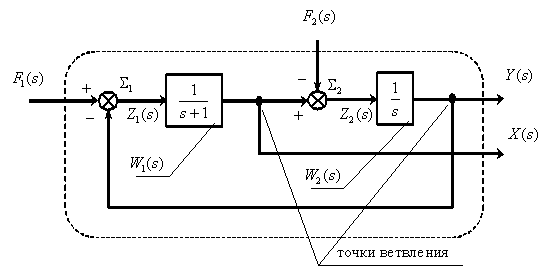
 . При этом схема эксперимента имеет вид –
. При этом схема эксперимента имеет вид –

 .
.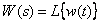
 ,
,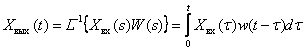 ,
, , тогда
, тогда .
. . При этом схема эксперимента имеет вид –
. При этом схема эксперимента имеет вид –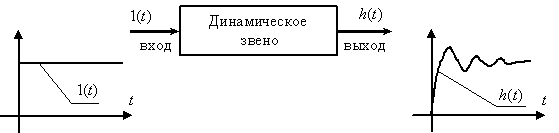

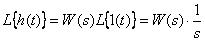 .
.
 .
.

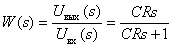 .
.
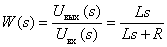 .
.

 , полученную путем формальной замены
, полученную путем формальной замены  на
на 
 . Тогда частотные спектры этих сигналов (преобразование Фурье) этих функций можно определить следующим образом –
. Тогда частотные спектры этих сигналов (преобразование Фурье) этих функций можно определить следующим образом –
 .
. .
. .
.
 .
. ,
,
 – действительная (вещественная) часть
– действительная (вещественная) часть  ,
, – мнимая часть
– мнимая часть  – модуль (амплитуда)
– модуль (амплитуда)  – фаза аргумент
– фаза аргумент  .
. .
.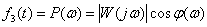 .
. .
. , построенный на комплексной плоскости при изменении частоты от 0 до
, построенный на комплексной плоскости при изменении частоты от 0 до  .
.
 .
.
 .
.
 .
. , тогда получаем
, тогда получаем .
. .
. .
. :
: