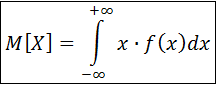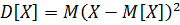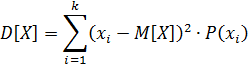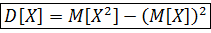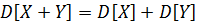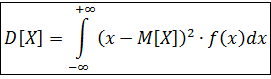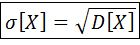Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Дискретная случайная величина. ⇐ ПредыдущаяСтр 3 из 3
1).Таблица: Ряд распределения(может быть конечным или бесконечным)
Так как события X=x1, X=x2…. попарно несовместны и составляют полную группу событий, следовательно
2).График: многоугольник распределения.
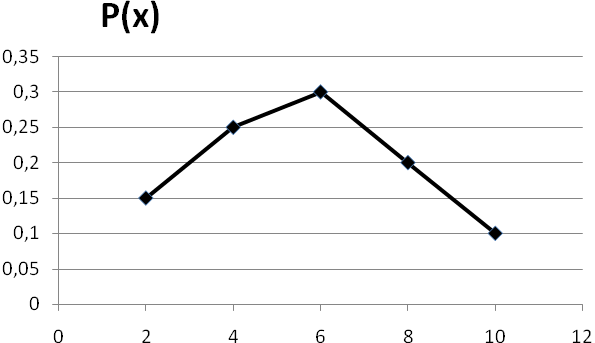
3).Функция распределения F(x0)– это вероятность того, что случайная величина X принимает значения меньшие или равные x0.
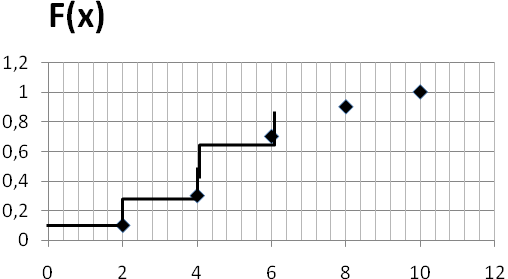
Вероятность попадания значения случайной величины в заданный интервал:
Пример:
F(4)=P(X≤4)=F(2)+F(4)=0,1+0,2=0,3 F(8)=P(X≤8)=F(2)+F(4)+F(6)+F(8)=0,1+0,2+0,4+0,2=0,9 P(4<X≤8)=F(8)-F(4)=0,9-0,3=0,6 Непрерывная случайная величина. 1).Таблица: Интервальный ряд распределения.
Где к – количество интервалов. 2).График: Гистограмма.
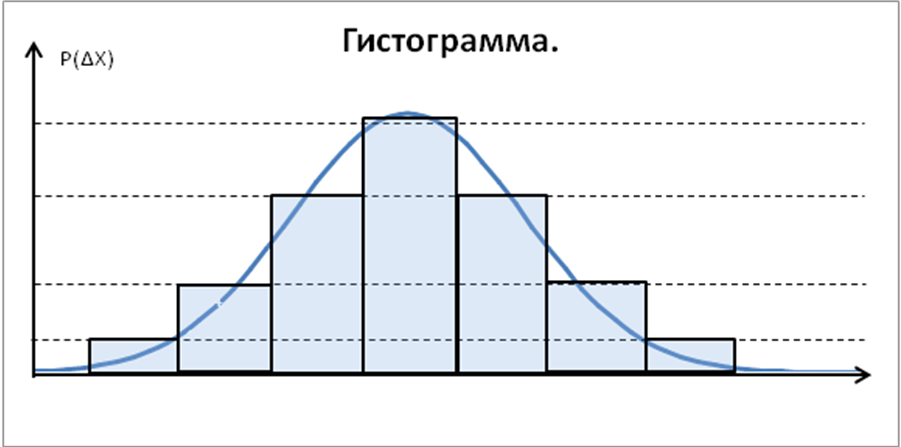
Функция распределения.
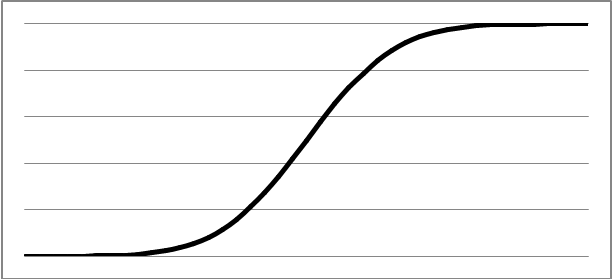 
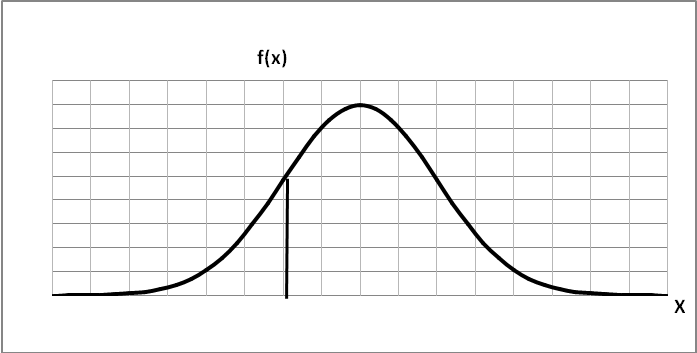
4). Функция плотности распределения f(x): (только для непрерывной случайной величины).
Найдём предел: Обозначим: . То есть функция распределения F(x) является первообразной для функции плотности распределения f(x).
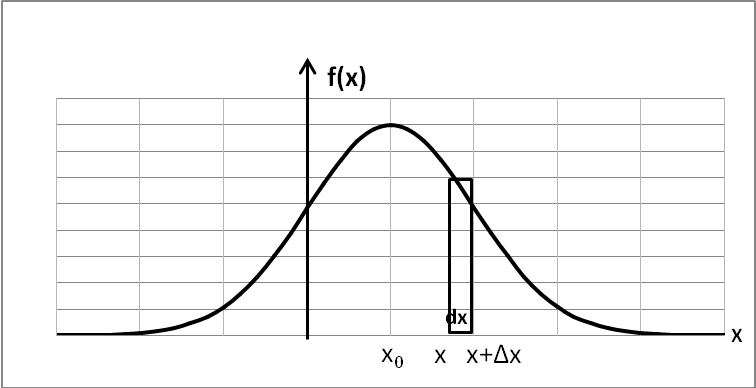
1). f(x) неотрицательная функция (f(x)≥0). 2). Вероятность попадания в элементарный интервал dx=(x+Δx)-x равна f(x)dx=dP.
3).Вероятность попадания случайной величины в интервал [a,b]:
4). Условие нормировки:
Числовые характеристики (параметры) случайной величины.
1). Математическое ожидание. Это среднее значение случайной величины.
. Пусть проведено nиспытаний, случайная величина приняла значение x1 -- m1 -- раз, x2 -- m2 -- раз, ………………….. Xk -- mk -- раз,где К -- количество различных значений, mi -- частота значения xi. m1+m2+…+mk=n Среднее арифметическое
Непрерывная случайная величина.
2). Дисперсия (рассеивание). Это математическое ожидание (среднее значение) квадрата отклонения случайной величины X от её математического ожидания.
Дискретная случайная величина.
Для вычисления дисперсии удобно пользоваться формулой:
Если X и Y независимые случайные величины,то
Непрерывная случайная величина.
Размерность дисперсии (единица измерения)2,поэтому используют: Средне -квадратическое или стандартное отклонение.
Контрольные вопросы.
Предмет теории вероятностей. Классификация случайных событий. Теоремы сложения вероятностей. Теоремы умножения вероятностей. Формула полной вероятности. Формулы Байеса. Дискретные и непрерывные случайные величины. Способы задания закона распределения случайной величины. Параметры распределения случайной величины. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 398. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
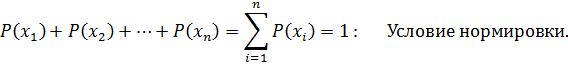
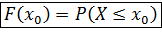
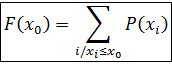
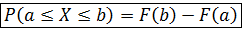
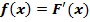
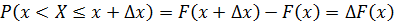
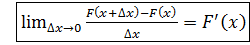
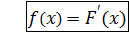 это функция плотности распределения.
это функция плотности распределения.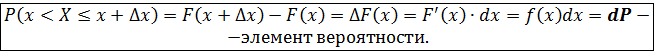
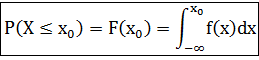
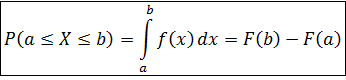
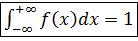 площадь под кривой равна единице.
площадь под кривой равна единице.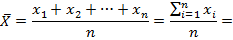
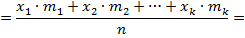
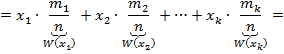 При n→∞ W(x1)→P(x1)
W(x2)→P(x2)
W(xk)→P(xk)
При n→∞ W(x1)→P(x1)
W(x2)→P(x2)
W(xk)→P(xk)
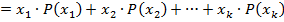 =
=
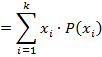
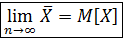
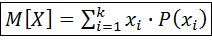
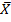 :
: