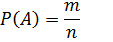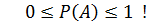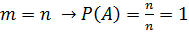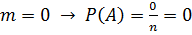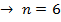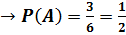Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Классическое определение вероятности.Стр 1 из 3Следующая ⇒ Основы теории вероятностей.
Теория вероятностей – это раздел математики, который изучает закономерности в массовых случайных событиях. Событие – это факт, который может произойти или не произойти в результате проведения опыта или испытания. Выделяют три вида событий: а) достоверные б) невозможные с) случайные Достоверное событие – это событие, которое обязательно произойдёт в результате данного опыта.( например: при бросании кубика выпадет 1≤целое число≤6). Невозможное событие – это событие, которое никогда не произойдет в условиях данного опыта. .( например: при бросании кубика выпадет число≥7, например 10). Случайное событие – это событие, которое может произойти или не произойти в результате данного опыта. ( например: бросили кубик один раз – выпадение числа 3 – случайное событие). События обозначаются первыми заглавными буквами латинского алфавита: А, В, С, D,. События называются массовыми, если они происходят одновременно в достаточно большом числе испытаний или многократно повторяются .( например: много людей бросают кубики или один человек бросает кубик много раз).
Классификация случайных событий.
Равновозможные события – это события такие, что ни одно из них не является более возможным, чем другие ( например: кубику всё равно на какую грань упасть). Совместные события – это события, которые могут произойти одновременно в результате данного опыта. ( например: бросаем 2 кубика - выпадение числа 1 и выпадение числа 3 – совместные события). Несовместные события – это равновозможные события такие, что появление одного из них исключает появление остальных.( например: бросаем 1 кубик – выпадение цифры 3 исключает выпадение остальных цифр).  Несколько случайных событий: Противоположные события Несмотря на то, что события случайные, при большом числе опытов они подчиняются закономерностям, которые изучает теория вероятностей.
Вероятность случайного события.
Вероятность случайного события Существуют два определения вероятности: классическое и статистическое, каждое из них имеет свои достоинства и недостатки. Классическое определение вероятности. Вероятность события
Если А – случайное событие, то
Если А – достоверное событие, то Если А – невозможное событие, то
Пример: при бросании кубика возможно 6 исходов Событие А: выпадет четное число. Число исходов, благоприятствующих событию А, m=3. Достоинства: можно вычислить вероятность не производя испытания. Недостатки: 1) не всегда известно число исходов опыта, 2) часто невозможно представить результат испытаний в виде равновозможных и несовместных событий. Поэтому на практике часто пользуются статистическим определением вероятности. |
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 349. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
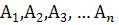 образуют полную группу событий, если каждое из них может произойти в результате данного опыта. ( например: выпадение чисел 1,2,3,4,5,6 –полная группа событий для бросания одного кубика).
образуют полную группу событий, если каждое из них может произойти в результате данного опыта. ( например: выпадение чисел 1,2,3,4,5,6 –полная группа событий для бросания одного кубика).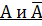 – это равновозможные несовместные события, образующие полную группу событий. Появление события
– это равновозможные несовместные события, образующие полную группу событий. Появление события 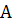 исключает появление события
исключает появление события 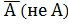 . ( например: орёл или решка, попадание в мишень или промах).
. ( например: орёл или решка, попадание в мишень или промах).