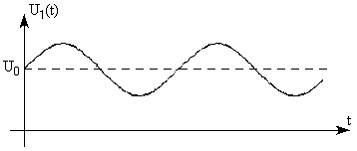
ОПИСАНИЕ ЛАБОРАТОРНОЙ УСТАНОВКИ

Лабораторная работа № 2

ИСЛЕДОВАНИЕ ЧАСТОТНОЙ МОДУЛЯЦИИ

Цель работы:Изучение работы частотного модулятора и спектра частотно модулированного сигнала. 

Теоретическая часть

Частотно-модулированный сигнал - это колебание, у которого мгновенная частота изменяется по закону модулирующего сигнала. Пусть модулирующий сигнал и несущее колебание изменяется, как показано на рис. 1 и 2.

Рис.1. Модулирующий сигнал.

Рис.2. Несущий сигнал.

Тогда мгновенная частота при частотной модуляции равна:

ω(t)=ω₀+ΔωcosΩt(1)

здесь Δω - девиация (отклонение) частоты под действием модулирующего сигнала, это отклонение в принципе пропорционально амплитуде модулирующего колебания. Мгновенную фазу частотно-модулированного сигнала найдем, проинтегрировавω (t) по времени:

Δφ=∫ω(t)dt = ω₀t +Δω/Ωsin Ωt (2)

В соответствии с рис.2 и выражением (1) частотно-модулированное колебание запишется в следующем виде:

U_чм=U_mcos(ω₀t+msinΩt) (3)

ГдеΔω/Ω=m - есть индекс частотной модуляции. Вид частотно – модулированного сигнала показан на рис. 3.

Рис.3. Частотно – модулированный сигнал.

Преобразуем выражение (3) по формуле косинуса суммы двух аргументов, получим:

U_чм(t)=U_m[cosω₀tcos(msinΩt) - sinω₀t sin(msinΩt)] (4)

Применим для выражений cos(m sin Ωt) и sin(m sin Ωt) преобразования по функциям Бесселя :

Тогда выражение (4) для частотно-модулированного сигнала будет иметь вид:

. (5)

Из (5) видно, что частотно – модулированный сигнал имеет дискретный спектр рис.4. с гармониками на частотах (ω₀± nΩ), где n=1, 2, 3, 4, 5…

Рис.4. Спектр частотно – модулированного сигнала.

Вид спектра модулированного колебания зависит от индекса частотной модуляции m, теоретически спектр бесконечен и содержит колебания несущей частоты и боковых составляющих первой и высших гармоник модулирующего сигнала, число которых бесконечно велико. Амплитуды боковых составляющих спектра пропорциональны бесселевым функциям, зависимость которых от индекса модуляции представлена на рис.5

Рис.5. Нормированная амплитуда составляющих спектра ЧМ сигнала в зависимости от индекса модуляции.

Графики беселевых функций показывают, что при малых индексах модуляции mпорядка 1, амплитуды высших гармонических составляющих спектра сигнала близки к нулю.С ростомm амплитуда несущей частоты сначала убывает до нуля, а боковые составляющие увеличиваются, и возрастает значимость высших гармоник. Происходит расширение полосы частот спектра. Дальнейшее увеличение mведет к волнообразному изменению амплитуды несущей частоты и еще большему расширению спектра.

Рассмотрим режим модуляции при малых и больших значениях m.Еслиm<<1, так что имеет место приближенные равенстваsin(msinΩt) ≈msinΩt, cos(msinΩt) ≈ 1,то выражение (4) переходит в следующее:

U_чм(t) ≈U_m(cosω₀t- msinΩtsinω₀t) = U_m[cosω₀t+ m/2cos(ω₀t+Ω)t–m/2cos(ω₀t-Ω)t](6)

Сравнивая (6) c уравнением для АМ колебания, у которого модулирующая функция такая же, как и при ЧМ, видим, что спектр колебаний состоит из несущей частоты ω₀и двух боковых частот: верхней ω₀ +Ωи нижней ω₀ –Ω.Ширина спектра равна - 2Ω,как и при амплитудной модуляции. Этот результат показывает, что при очень маленьких девиациях Δω (по сравнению с Ω) ширина спектра от Δω не зависит.При возрастании mуравнение (6) не дает правильного представления о действительной картине явлений при частотной модуляции. Для получения правильной картины необходимо учитывать боковые частоты высших порядков в соответствии с выражением(5).

При значениях индекса mот 0.5 до 1 приобретает некоторое значение вторая пара боковых частот, ввиду чего ширина спектра должна быть приравнена 4Ω. Далее, при 1<m<2 приходиться учитывать третью и четвертую пары боковых частот и т.д.На рис.6 показаны спектры сигналов с ЧМ для трех значений индекса модуляции 1, 2.5, 4 и 5.

Рис.6. Спектры ЧМ колебаний. Зависимость спектров от индекса модуляции ( а) m=1; б) m=2.5; в) m=4; г) m=5). ; где - девиация частоты, F- частота модулирующего сигнала).

Из приведенных примеров следует, что ширина спектра практически может быть ограничена боковыми частотами, которые образуются гармониками с номером, равнымm.Рассмотрим теперь большие значения m.Вопрос сводиться к выяснению зависимости бесселевой функции J_n(m)от порядкового номера n при больших значениях аргумента m. Оказывается, что при m>>1 величина | J_n(m)| более или менее равномерна при всех целых значениях |n|, меньших, чем аргумент m. При |n|, близких к m, | J_n(m)|образует всплеск, а придальнейшем увеличении |n| функция | J_n(m)|быстро убывает до нуля. Общий характер этой зависимости показан на рис.7 для m=100. Из рисунка видно, что наивысший номер nбоковой частоты, которую еще необходимо принимать в расчет, приблизительно равен индексу модуляции m(в данном случае n=100).В практической радиотехнике различают широкополоснуюm>>1 (Δω>>Ω) и узкополосную m≤1 (Δω<<Ω) частотную модуляцию. С определенной долей приближения, в первом случае, как правило, учитывают составляющие с номерами n≤ m+1 . Это соответствует ши­рине спектра ЧМ колебания при гармонической модуляции в которой сосредоточено 99 % энергии сигнала – 2(Δω+Ω)≈2 Δω.

При небольших индексах ЧМ (от 1 до 2.5) пользуютсяфор­мулой -2Ω(1+m+√m).

Рис.7. Ширина спектра ЧМ колебания при больших значениях индекса модуляции.

За пределами этой полосы амплитуда составляющих в 100 раз меньше амплитуды немодулированной несущей.

    В некоторых случаях(m=4~10)для определения ши­рины спектра ЧМ сигналаможно воспользоваться фор­мулой -2Δω+2Ω.Основное применение ЧМ - высококачественное радиовещание (при девиации частоты ~100KHz - т.е. с m≈4) в диапазоне УКВ (60-100MHz) и в каналах передачи звука в телевещании. Причина - низкая чувствительность к паразитной амплитудной модуляции и к помехам.Поскольку спектр ЧМ сигнала шире, чем при АМ, помехоустойчивость такой модуляции выше. Применяется ЧМ по причине своей широкополосности в основном в диапазоне метровых и более коротких волн. Узкополосная ЧМ (Narrow Frequency Modulation - NFM) используется в системах мобильной связи, широкополосная (Wide Frequency Modulation — WFM) в радио- и телевещании. При стереофоническом вещании в модулирующем сигнале имеется поднесущая с дополнитель­ной модуляцией в зависимости от стандарта вещания. Кроме того ЧМ с m≈2 широко применялась в системах радиорелейной и спут­никовой связи, модуляция несущей осуществлялась широкополосным групповым сигналом, но в настоящее время, такие сигналы практиче­ски вытеснены цифровыми.

В радиолокации ЧМ используется как внутриимпульсная в вариан­тах линейной ЧМ(ЛЧМ), симметричной, зигзагообразной и др.

ОПИСАНИЕ ЛАБОРАТОРНОЙ УСТАНОВКИ

Установка содержит формирователь УКВ-ЧМ сигнала, в котором предусмотрена возможность подачи внешнего модулирующего сигнала, низкочастотный генератор, аттенюатор и анализатор спектра.

ДОМАШНЕЕ ЗАДАНИЕ

1.Изучить теоретическую часть.

2.Ознакомиться с порядком выполнения лабораторной работы.

3.Подготовиться к ответам на контрольные вопросы.

КОНТРОЛЬНЫЕ ВОПРОСЫ

1.Дайте определение частотной модуляции.

2.Что такое "девиация"?

3.Что такое "индекс модуляции"? От чего он зависит и от чего не зависит?

4.Чем определяется ширина спектра ЧМ сигнала?

5. В чем отличие спектра ЧМ от АМ при малых (m < 1) индексах модуляции?

6.Почему частота модулирующего сигнала должна быть меньше частоты несущего колебания?

7. Во сколько раз ширина спектра радиосигнала с АМ модуляцией больше спектра первичного модулирующего сигнала?

8.В чем преимущества ЧМ модуляции по сравнению с АМ модуляцией и в чем её недостатки?

9.Какова практическая зависимость эффективной ширины спектра ЧМ радиосигнала в зависимости от девиации частоты несущей?

ЛАБОРАТОРНОЕ ЗАДАНИЕ