
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Изучение электростатических полей,Созданных системой проводящих электродов Для создания электростатических полей обычно применяется система металлических электродов, часть которых (или все) находятся под определенными потенциалами
Применим теорему Гаусса
для электростатического поля к кубу с ребрами
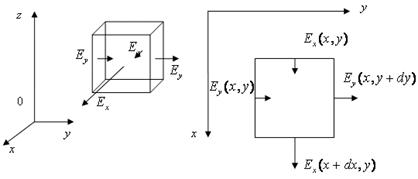
Рис. 1.5. Применение теоремы Гаусса для плоского (двумерного) электрического поля
Отношение потока вектора
где
Из формулы (1.11) следует
Подстановка последних выражений в уравнение (1.15) приводит к двумерному уравнению Лапласа
Функции, являющиеся решениями уравнения Лапласа
называются гармоническими функциями, они играют важную роль во многих задачах физики и математики.  Для получения единственного решения
где
Задачи, подобные (1.18), (1.20), (1.21) называются краевыми задачами. Их аналитическое решение возможно не всегда, поэтому часто приходится применять компьютерные вычисления. В качестве примера рассмотрим поле, созданное двумя плоскими электродами М и N на токопроводящей бумаге прямоугольной формы. Пусть данному случаю отвечают граничные условия: на электроде M φ=0, (1.22) на электроде N φ=U, (1.23) на краях токопроводящей бумаги Последнее условие вызвано следующим. Вблизи края токопроводящей бумаги электрический ток, обусловленный направленным движением электронов, направлен параллельно краю. Следовательно, и вектор
Это условие называют условием отражающего экрана. Решение уравнения Лапласа (1.18) для двух плоских электродов и граничных условий (1.26)-(1.28)
где
Из последнего выражения находится
|
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 469. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 . Распределение зарядов при этом неизвестно, что не позволяет применить принцип суперпозиции (1.35) для напряженностей электростатического поля. Поэтому необходимо использовать уравнения непосредственно для потенциала φ. Рассмотрим их для примера плоского (двухмерного) поля, когда
. Распределение зарядов при этом неизвестно, что не позволяет применить принцип суперпозиции (1.35) для напряженностей электростатического поля. Поэтому необходимо использовать уравнения непосредственно для потенциала φ. Рассмотрим их для примера плоского (двухмерного) поля, когда ,
,  . (1.12)
. (1.12) , (1.13)
, (1.13) , параллельными осям координат, расположенному вне электродов и электрических зарядов на них (рис. 1.5). Объем куба
, параллельными осям координат, расположенному вне электродов и электрических зарядов на них (рис. 1.5). Объем куба  , площадь грани
, площадь грани  .
.
 (1.14)
(1.14) через поверхность к объему
через поверхность к объему 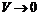 называется дивергенцией вектора
называется дивергенцией вектора  , (1.15)
, (1.15) – составляющая вектора
– составляющая вектора  (1.16)
(1.16) . (1.17)
. (1.17) . (1.18)
. (1.18)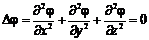 . (1.19)
. (1.19) уравнение Лапласа (1.18) должно быть дополнено граничными условиями. В частности, на поверхности проводящих (металлических) электродов потенциал постоянен и равен поданному на него потенциалу
уравнение Лапласа (1.18) должно быть дополнено граничными условиями. В частности, на поверхности проводящих (металлических) электродов потенциал постоянен и равен поданному на него потенциалу , (1.20)
, (1.20) – уравнения линий, описывающих форму электродов. В некоторых случаях задается значение производной по нормали к линии
– уравнения линий, описывающих форму электродов. В некоторых случаях задается значение производной по нормали к линии  . Например, задается нулевое значение такой производной
. Например, задается нулевое значение такой производной . (1.21)
. (1.21) напряженности электрического поля также направлен параллельно краям листа, а его составляющая, направленная вдоль нормали к краю, равна нулю
напряженности электрического поля также направлен параллельно краям листа, а его составляющая, направленная вдоль нормали к краю, равна нулю . (1.25)
. (1.25) , (1.26)
, (1.26)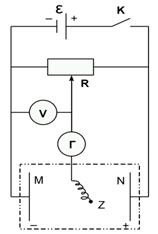 линейно зависит лишь от одной переменной. Поэтому его можно представить в виде
линейно зависит лишь от одной переменной. Поэтому его можно представить в виде , (1.27)
, (1.27) (1.28)
(1.28) .
.