
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Случай 1.Система устойчива в разомкнутом состоянии.Передаточная функция разомкнутой системы имеет вид:
Этот случай соответствует сигналам автоматического управления без астатизма. Введем вспомогательную функцию:
где Подставим в (2)
Это значит, что годограф
Вернемся теперь к функции,
Формулировка частотного критерия Найквиста. Если разомкнутая система устойчива, то для устойчивости замкнутой системы необходимо и достаточно, чтобы амплитудно-фазо-частотная характеристика разомкнутой системы не охватывала точку Первый график (рис. 9) соответствует случаю, когда устойчивость системы нарушается только с увеличением общего коэффициента усиления разомкнутой системы. Второй график (рис. 10) соответствует случаю, когда уменьшение к может привести к неустойчивости замкнутой системы (с уменьшением к меняются радиусы-векторы всех точек характеристики). Годографы неустойчивых систем.
Имея в виду очертания амплитудно-фазовых характеристик, к сформулированному критерию устойчивости добавим разъяснения, что значит «не охватывает точки с координатами  Характеристика может пересекать отрицательную ось левее точки
Случай 2. Система нейтральна в разомкнутом состоянии. Характеристический полином разомкнутой системы
Это соответствует системам с астатизмом порядка
Подстановка
В случае
Для сложных очертаний годографа Найквиста в число отрицательных переходов надо включать и переход пунктирной окружности бесконечно большого радиуса при Случай 3. Система неустойчива в разомкнутом состоянии. Пусть характеристический многочлен
при замене
при изменении частоты Задание: Задания выполняются по вариантам из курсовой работы 1. Изучить предложенную функциональную схему. 2. Определить передаточные функции звеньев и составить структурную схему. 3. Ввести параметры звеньев и определить передаточную функцию замкнутой системы. 4. Рассчитать теоретически и построить годограф Михайлова. 5. Определить устойчивость системы, используя критерий Найквиста.
|
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 379. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 ,
,  (1)
(1) , (2)
, (2) - характеристический полином замкнутой системы;
- характеристический полином замкнутой системы;  - характеристический полином разомкнутой системы.
- характеристический полином разомкнутой системы. , получим
, получим  . По критерию Михайлова изменение аргумента
. По критерию Михайлова изменение аргумента  при
при 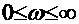 равно
равно  , т.к. предполагается, что разомкнутая цепь устойчива. С другой стороны требуется, чтобы система была устойчива в замкнутом состоянии. Для этого нужно потребовать, чтобы изменение аргумента
, т.к. предполагается, что разомкнутая цепь устойчива. С другой стороны требуется, чтобы система была устойчива в замкнутом состоянии. Для этого нужно потребовать, чтобы изменение аргумента  при
при  должно быть равно
должно быть равно .
.
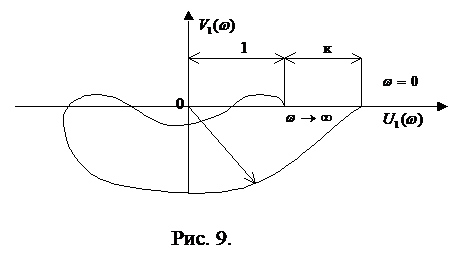
 , которая представляет собой амплитудно-фазовую частотную характеристику разомкнутой системы (рис. 10 и рис 11).
, которая представляет собой амплитудно-фазовую частотную характеристику разомкнутой системы (рис. 10 и рис 11).

 .
.


 ,
,  . Рассмотрим случай, когда
. Рассмотрим случай, когда  , тогда
, тогда 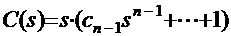 . Плоскость корней
. Плоскость корней 
 означает перемещение вдоль оси
означает перемещение вдоль оси  от точки 0 вверх. При этом, чтобы все корни оставить слева, обойдем точку 0 по окружности малого радиуса
от точки 0 вверх. При этом, чтобы все корни оставить слева, обойдем точку 0 по окружности малого радиуса  , тогда
, тогда  ;
;  . И при
. И при  получим
получим  ;
;  при
при  .Следовательно, точки
.Следовательно, точки  соответствует
соответствует  окружности бесконечно большого радиуса в плоскости корней
окружности бесконечно большого радиуса в плоскости корней  . Поскольку при этом все корни
. Поскольку при этом все корни  .
.
 аналогично получается та же формулировка критерия – не охват точки
аналогично получается та же формулировка критерия – не охват точки 
 корней с положительной действительной частью. Тогда функция
корней с положительной действительной частью. Тогда функция
 на
на  , согласно критерию Михайлова для устойчивости замкнутой системы должна иметь следующее изменение аргумента
, согласно критерию Михайлова для устойчивости замкнутой системы должна иметь следующее изменение аргумента
 от 0 до
от 0 до  . Это значит, что для устойчивости замкнутой системы требуется, чтобы амплитудно-фазо-частотная характеристика разомкнутой цепи охватила точку
. Это значит, что для устойчивости замкнутой системы требуется, чтобы амплитудно-фазо-частотная характеристика разомкнутой цепи охватила точку  , где
, где  .
.