
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Формулировка критерия Михайлова.Стр 1 из 3Следующая ⇒ Лабораторная работа № 8. Частотные критерии устойчивости (Михайлова, Найквиста).
Время выполнения работы: 2 часа
Цель работы: изучить частотные критерии устойчивости (Михайлова, Найквиста) и научиться их использовать.
Содержание: · Цель работы · Краткие сведения из теории · Критерий устойчивости Михайлова · Критерий устойчивости Найквиста. · Задание · Отчет по лабораторной работе · Контрольные вопросы
Краткие сведения из теории: Частотные критерии устойчивости позволяют судить об устойчивости систем автоматического управления по их частотным характеристикам. Эти критерии являются графоаналитическими и получили широкое распространение, так как позволяют сравнительно легко исследовать устойчивость систем высокого порядка, а так же имеют простую геометрическую интерпретацию и наглядность. Мы рассмотрим два частотных критерия устойчивости: критерий Михайлова и критерий Найквиста. Критерий устойчивости Михайлова
Критерий устойчивости Михайлова относится к частотным критериям и используется для исследования устойчивости замкнутых систем. Рассмотрим замкнутую систему управления структурная схема которой имеет вид
Пусть передаточная функция разомкнутой системы равна
и пусть Передаточная функция замкнутой системы
Полином
Составим характеристический полином замкнутой системы
Если подставим в
В последнем равенстве выделим действительную и мнимую части комплексного числа: 
где
На плоскости Формулировка критерия Михайлова. Для того, чтобы замкнутая система автоматического управления была устойчива, необходимо и достаточно чтобы годограф Михайлова при изменении частоты
Заметим, что для устойчивых систем автоматического управления годограф Михайлова начинается при Кроме того, для устойчивых систем фаза Кривая Михайлова для устойчивых систем всегда плавную спиралевидную форму, причём конец её ( Признаком неустойчивости системы является нарушение числа и последовательности пройденных кривой Михайлова квадрантов координатной плоскости, вследствие чего угол поворота вектора Примеры годографов Михайлова для неустойчивых систем:
Критерий устойчивости Найквиста. Частотный критерий устойчивости Найквиста базируется на частотных характеристиках разомкнутых систем управления. Он дает правила, согласно которых по виду частотных характеристик разомкнутой системы можно судить об устойчивости замкнутой системы.
|
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 806. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |


 – степень полинома
– степень полинома  ,
,  – степень полинома
– степень полинома  .
. .
. - имеем степень
- имеем степень  .
. . (1)
. (1)
 , то получим комплексное число
, то получим комплексное число .
. , (2)
, (2) . (3)
. (3)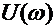 и
и  комплексное число
комплексное число  изображается вектором
изображается вектором  (см. рис. 2). При из изменении частоты
(см. рис. 2). При из изменении частоты  от 0 до
от 0 до  вектор
вектор  на вещественной положительной полуоси, обходил последовательно
на вещественной положительной полуоси, обходил последовательно 
 все коэффициенты характеристического полинома положительны и
все коэффициенты характеристического полинома положительны и  .
. с ростом частоты
с ростом частоты  ,являющиеся слагаемыми вектора
,являющиеся слагаемыми вектора  ) уходит в бесконечность в том квадранте координатной плоскости, номер которого равен степени характеристического полинома.
) уходит в бесконечность в том квадранте координатной плоскости, номер которого равен степени характеристического полинома. .
.