
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Критерий устойчивости ГурвицаСтр 1 из 2Следующая ⇒ Лабораторная работа № 7. Алгебраические критерии устойчивости (Гурвица и Рауса). Время выполнения работы: 2 часа
Цель работы: изучить алгебраические критерии устойчивости (Гурвица и Рауса) и научиться их использовать.
Содержание: · Цель работы · Краткие сведения из теории: · Критерий устойчивости Гурвица · Критерий устойчивости Рауса · Задание: · Отчет по лабораторной работе: · Контрольные вопросы
Краткие сведения из теории: Прямой метод анализа устойчивости систем, основанный на вычислении корней характеристического уравнения очень сложен, особенно для уравнений высоких степеней. Поэтому в инженерной практике приобретают правила, которые позволяют определять устойчивость системы без вычисления корней. Эти правила называются критериями устойчивости. С помощью критериев устойчивости можно не только установить, является ли система устойчивой или нет, но и выяснить, как влияют на устойчивость те или иные параметры и структурные изменения в системе. Различают две группы критериев устойчивости: алгебраические (Рауса и Гурвица), основанные на анализе коэффициентов характеристического уравнения и частотные (Михайлова и Найквиста), основанные на анализе частотных характеристик. Частотные критерии позволяют оценивать устойчивость системы, даже если в наличии имеются экспериментальные частотные характеристики, а уравнения динамики неизвестны. Критерий устойчивости Гурвица Этот критерий позволяет сказать, где на комплексной плоскости расположены корни характеристического уравнения. Пусть имеем характеристическое уравнение: 
Сначала строим главный определитель Гурвица по следующему правилу: по главной диагонали определителя слева направо выписываются все коэффициенты характеристического уравнения от С1 до Сn в порядке возрастания индекса. Столбцы вверх от главной диагонали дополняются коэффициентами характеристического уравнения с последовательно возрастающими индексами, а столбцы вниз с последовательно убывающими индексами. На место коэффициентов с индексами больше n (где n – порядок характеристического уравнения) и меньше нуля проставляются нули.
Далее выделяем в главном определителе Гурвица главные диагональные миноры и получаем определители Гурвица низшего порядка. Номер определителя зависит от номера коэффициента по диагонали, до которого составляют данный определитель.
В итоге проверяется n определителей, которые являются главными диагональными минорами матрицы Гурвица. Определение: чтобы САУ была устойчива, необходимо и достаточно, чтобы определитель Гурвица и его диагональные миноры имели знаки, одинаковые со знаком первого коэффициента СО характеристического уравнения, т.е. были положительными, так как всегда СО можно выбрать положительным. Т.е. при СО > 0, Условия устойчивости 1. Система первого порядка Характеристическое уравнение первого порядка:
Система будет устойчива, если все коэффициенты уравнения положительны. 2. Система второго порядка Характеристическое уравнение:
Определитель Вывод: для устойчивой системы второго порядка все коэффициенты характеристического уравнения должны иметь один и тот же знак.
3. Система третьего порядка. Характеристическое уравнение:
Главный определитель:
По Гурвицу Минор второго порядка:
Воспользуемся правилом Саррюса и определим:
Чтобы условие выполнялось, нужно, чтобы C3>0 и чтобы Вывод: чтобы система третьего порядка была устойчива, необходимо и достаточно, чтобы:
4. Система четвертого порядка
Полагая, что знаки выбраны так, чтобы Главный определитель
Так как Чтобы Чтобы Раскроем определитель
То есть, Или
Вывод: чтобы система четвертого порядка была устойчива, необходимо и достаточно, чтобы соблюдались следующие условия:
Сложности использования критерия Гурвица возрастают с ростом порядка полинома. Считается, что эффективное использование критерия Гурвица возможно при n < 4, так как при больших размерностях число проверяемых условий стремительно возрастает. |
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 255. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |



 >0,
>0, 

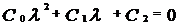


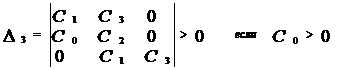








 , то
, то 
 , нужно, чтобы
, нужно, чтобы  , нужно, чтобы
, нужно, чтобы 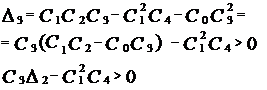
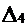 . Для этого разложим его на адьюнкты первой строки:
. Для этого разложим его на адьюнкты первой строки:


