
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Закон распределения как модель формирования размера в партии деталей
Рассеяние величины А (размера конструктивного элемента детали) в партии деталей характеризуется прежде всего полем рассеяния ωА, которое определяется как разность максимального и минимального значений: ωА = Аmax - Amin (1) Вторая характеристика должна определить положение поля рассеяния относительно конца номинального значения показателя А0. Это можно сделать с помощью любого из трех отклонений: минимального (нижнего) EIω, максимального (верхнего) ESω или координаты середины поля рассеяния (среднего) EСω, как это показано схемой на рис. 2. Всю совокупность значений показателя А(размера элемента конструкции детали)в партии обработанных деталей можно описать одним из следующих наборов трех величин: 1 вариант - А0 , EIω, ESω 2 вариант - А0, EIω, ωА 3 вариант - А0, ESω, ωА 4 вариант - А0, ECω, ωА 5 вариант - А0, Amax, Amin
Рис. 2. Схема характеристик рассеяния размера элемента в партии деталей после обработки
В этих наборах номинальное значение размера элемента А0 координата середины поля рассеяния ECω описывают уровень качества, а поле рассеяния ωА (EIω, ESω) дают представление о достигнутой в партии изготовленных изделий стабильности значения этого показателя. Очевидно, что для описания требуемого качества вместо поля рассеяния и его координаты необходимо задать поле допуска ТА и одну из его координат (например, ЕС). Варианты описания значений показателя в партии машин различаются формой задания полей рассеяния и допуска и в случае необходимости легко преобразуются один в другой по формулам, приведенным в табл. 1. 
Таблица 1. Формулы для перехода от одной формы задания показателя служебного назначения к другой
Важной характеристикой рассеяния величины показателя А служит распределение его значений по полю рассеяния ωА. Распределение – это совокупность значений показателя, расположенных возрастающем порядке с указанием частоты их повторения. Для оценки частоты повторения значений используют: · частоту - количество mi значений Ai в партии, · частость – отношение количества mi значений Ai к их общему количеству n в партии, · вероятность P(x) – количество значений Ai в процентах от общего их числа. Распределение значений показателя служебного назначения может быть представлено в виде таблицы или графика. Для построения таблицы и графика поле рассеяния ωА, рассчитанное по формуле (1), разбивают на несколько равных интервалов и подсчитывают количество mi значений, которые попадают в каждый интервал. По результатам этой работы заполняют таблицу, в которой располагают интервалы в порядке возрастания значений показателя. Пример такого представления распределения 100 значений размеров деталей, обработанных в одной технологической системе и рассеянных по полю ωА = 0,35 мм, приведен в табл. 2. Информация о распределении из табл.2 может быть представлена графически в виде диаграммы, представленной на рис. 3. Для этого по оси абсцисс откладывают значение показателя (размера в рассматриваемом примере) и отмечают границы интервалов в соответствии с табл. 2. По оси ординат откладывают частоты mi, частости
Таблица 2. Распределение размеров в партии обработанных деталей
Рис. 3. Распределение размеров в партии обработанных деталей Если увеличивать количество значений показателя (измеренных размеров деталей) при уменьшении величины интервала (устремив его к нулю), ломаная линия полигона распределения превращается в плавную кривую, называемую кривой распределения (см. рис.4). Эта кривая графически представляет дифференциальный закон распределения (плотность вероятности) непрерывной случайной величины, аналитическое выражение которого описывается функцией y = f (x), (2) где х – текущее значение случайной величины (нашего показателя служебного назначения машины А); y - значение ординаты кривой рассеяния, соответствующей текущему значению xi=Аi случайной величины, (т.е. частота, частость или вероятность текущего значения случайной величины). Зная этот закон можно определить вероятность того, что значение случайной величины x окажется в интервале от а до b:
В графическом представлении вероятность будет равна площади участка с основанием аb, ограниченного сверху кривой распределения, как это показано на рис.4.
Рис. 4. График дифференциального закона распределения случайной величины
При a=-∞ и b=+∞ Во многих теоретических и практических задачах для количественного описания распределения используют следующие числовые характеристики: · положение центра группирования случайной величины (центром группирования случайной величины называют ее среднее значение, около которого в основном располагаются все ее остальные значения) характеризуют математическим ожиданием М(х), средним арифметическим значением Xср случайной величины или средним арифметическим отклонением от номинального значения Х0: Еmх = Xср - Х0; · меру рассеяния характеризуют полем рассеяния ω, дисперсией и средним квадратическим отклонением σx. Математическое ожидание дискретной случайной величины (каковой является, например, размер конструктивного элемента в партии обработанных деталей):
где k – количество возможных значений случайной величины х. Математическое ожидание непрерывной случайной величины:
В практических задачах, решаемых в технологии машиностроения, положение центра группирования характеризуют средним арифметическим значением случайной величины:
где: mi – частота отдельных значений xi ; k – количество отдельных значений xi ; n – общее количество значений xi. Центр группирования или среднее значение случайной величины не всегда совпадает с серединой поля рассеяния (рис. 5), его координата М(х) относительно конца номинального значения: М(х) = Хср - Х0 ≠ ECωx. (6)
Рис. 2.5. Смещение центра группирования случайной величины Х относительно середины поля рассеяния
Смещение центра группирования относительно середины поля рассеяния оценивается коэффициентом относительной асимметрии α:
Одной из характеристик рассеяния значений случайной величины вокруг центра группирования M(x) служит дисперсия Dx. Дисперсия дискретной случайной величины:
Дисперсия непрерывной случайной величины:
В практике для оценки степени рассеяния случайной величины используют среднее квадратическое отклонение, равное положительному квадратному корню из дисперсии:
Для практических распределений положение центра группирования характеризуют средним арифметическим значением случайной величины и тогда среднее квадратическое отклонение равно:
Таким образом, чтобы охарактеризовать распределение случайной величины используют следующий набор числовых характеристик: · номинальное значение случайной величины Х0 (например, номинальный размер); · поле рассеяния случайной величины ωх; · координата середины поля рассеяния (центральное отклонение) ECω; · среднее арифметическое значение случайной величины Хср или среднее арифметическое отклонение Еmх; · Если кривая распределения симметрична относительно среднего арифметического значения, центр группирования оказывается совмещенным с координатой середины поля рассеяния, т. е. ECωx = Еmх.
Законы распределения Распределения случайных величин в зависимости от условий могут описываться разными законами. Многочисленными исследованиями ученых-технологов из всего разнообразия выявлено ограниченное их количество, достаточно адекватно описывающее результаты технологических процессов машиностроения. Из этих законов наибольшее практическое значение имеет закон нормального распределения или закон Гаусса. Это объясняется тем, что в технологических процессах машиностроительного производства на результат оказывает влияние большое количество отклоняющих факторов, причем большинство из них влияют примерно в одинаковой степени. Согласно известному положению теории вероятностей распределение суммы большого количества взаимно независимых случайных слагаемых величин при отсутствии доминирующих факторов подчиняется закону Гаусса. Уравнение кривой нормального распределения имеет следующий вид:
Анализ этого уравнения показывает, что кривая нормального распределения симметрична относительно центра группирования, представляемого величинами М(х) или Хср. Координата центра группирования определяет положение кривой относительно начала отсчета (например, относительно номинального значения показателя Х0), а среднее квадратическое отклонение σ – ее форму и размах. Значениям х и –х соответствует одинаковая величина ординаты y. При х = Хср кривая имеет максимум:
На расстоянии ±σ от вершины (см. рис. 2.6) кривая имеет две точки (точки А и В) перегиба, ордината которых:
Рис.2.6. Кривая закона нормального распределения (Гаусса)
Кривая асимптотически приближается к оси абсцисс. На расстоянии ±3σ от вершины кривой ее ветви настолько близко подходят к оси абсцисс, что в этих пределах оказывается 99,73% от площади под всей кривой. При практических расчетах обычно принимается, что поле рассеяния ωх = 6σх (2.10) и в пределах этого поля находятся все значения исследуемой случайной величины. Возникающая при этом погрешность составляет 0,27% и считается допустимой. Из формулы (2.10) следует, что с увеличением σх пропорционально растет поле рассеяния, как это показано на рис. 2.7.
Рис. 2.7. Влияние среднеквадратического отклонения на форму кривой нормального распределения
Поэтому среднее квадратичное отклонение и считается мерой рассеяния или мерой точности; применительно к нашей теме это отклонение можно считать мерой нестабильности показателя служебного назначения машины. С помощью закона Гаусса адекватно описываются результаты производственных процессов с достаточно большой повторяемостью, т.е. в условиях массового и крупносерийного производств машин. В условиях единичного и мелкосерийного производств, где повторяемость отсутствует или чрезвычайно мала, возможность получения единичного результата становится одинаково возможной в пределах возможного или допустимого поля рассеяния. При необходимости обеспечить (достичь) особо высокую стабильность результата (например, при обработке деталей по 5-6 квалитетам точности) вероятность его попадания в узкие границы поля допуска по наименьшему, среднему или наибольшему значениям становится одинаковой. В этих случаях применяют закон равной вероятности.Такое распределение формируется также, когда в технологической системе есть один доминирующий фактор и этот фактор изменяет получаемый размер по линейному закону. Примером такого фактора может служить размерный износ инструмента, описываемый линейной функцией аргумента времени его работы. Графически закон равной вероятности представляется прямоугольником с основанием ωх = xmax - xmin и высотой
Рис. 2.8. Распределение случайной величины по закону равной вероятности
В условиях серийного производства результат соединения двух или нескольких деталей, размеры которых рассеяны по закону равной вероятности, распределение их общего размера долее адекватно описывается законом равнобедренного треугольника (законом Симпсона). Этот закон также применяют также для описания распределений размеров 7-8 квалитетов точности, полученных при обработке на станках. Графически этот закон представляется равнобедренным треугольником с основанием, равным полю рассеяния ωх (см. рис. 2.9.).
Рис. 2.9. Распределение случайной величины по закону Симпсона
Распределение оказывается симметричным относительно
И среднее квадратическое отклонение Распределения по законам Симпсона и равной вероятности можно рассматривать как отклонения от закона нормального распределения, количественно степень этих отклонений оценивается коэффициентом λ, который называют относительным средним квадратическим отклонением:
Таблица 2.3. Значения относительного среднего квадратического отклонения
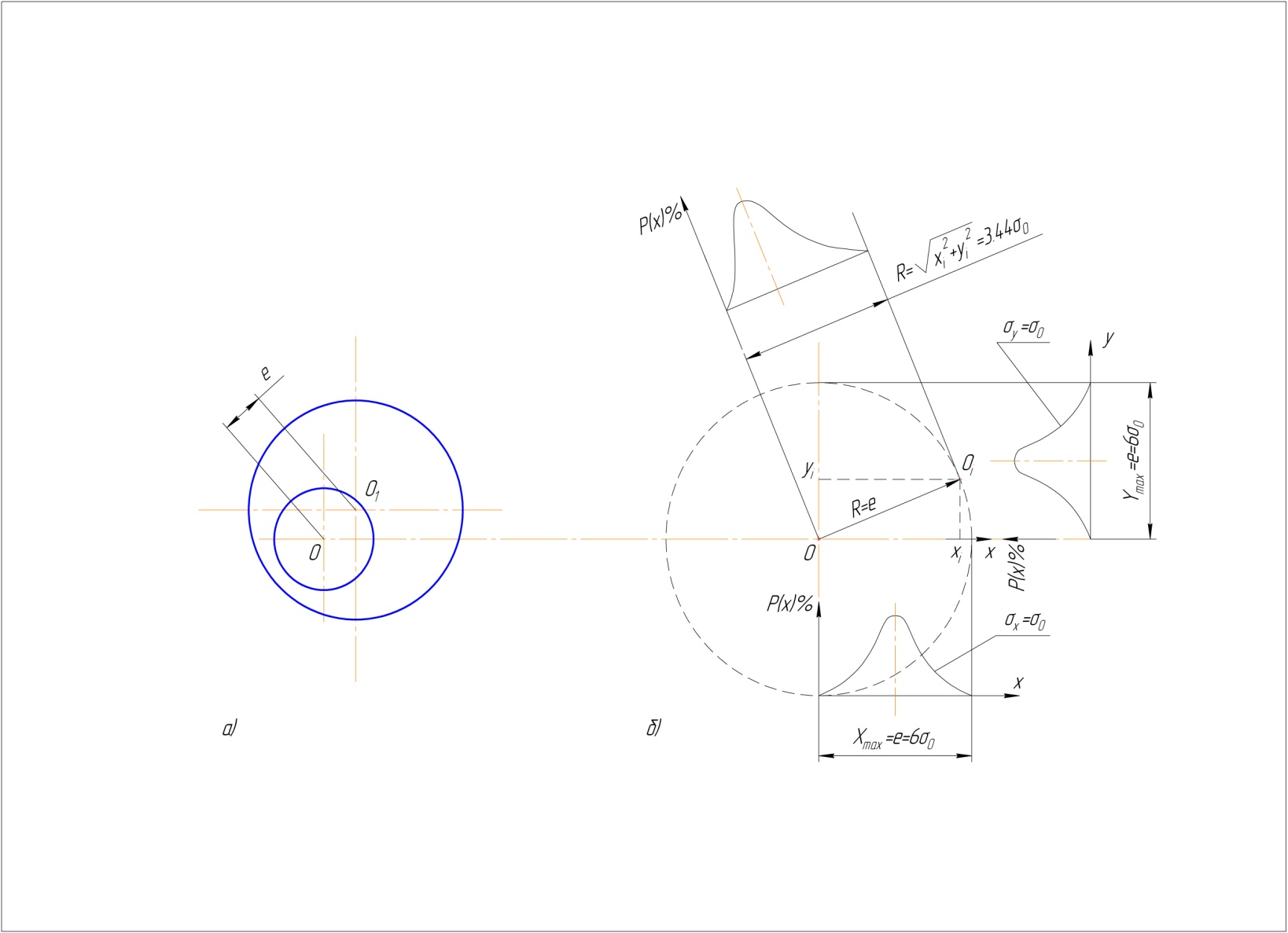
Закон эксцентриситета (закон Релея).Этим законом описывается распределение таких сугубо положительных по величине погрешностей как эксцентриситет, радиальное биение, эллипсность, непараллельность и т.п. Формирование этого распределения хорошо иллюстрируется образованием эксцентриситета наружной и внутренней цилиндрических поверхностей при обтачивании поверху и установке на оправку с гарантированным зазором. Схема такого процесса приведена на рис. 2.10. На рис. 2.10а приведена деталь типа диска, наружная поверхность которого получается с некоторым эксцентриситетом е относительно оси отверстия О. Эксцентриситет представляется радиусом-вектором R = е, который может бытьравновероятно направлен под любым углом к оси ОХ. На рис. 2.10б показано текущее положение радиуса-вектора R, описываемое текущими значениями координат его конца хi и уi.
Рис.2.10. Схема формирования распределения по закону Релея эксцентриситета отверстия и наружного цилиндра
Особенностью такого распределения является то, что в его основе лежит распределение координат по закону Гаусса (нормального распределения), а распределение эксцентриситета нормальным не является, как это показано на рис. 2.10б. Уравнение закона Релея имеет следующий вид:
где σ0 – среднее квадратическое отклонение значений координат X и Y. Поле рассеяния переменной величины радиуса-вектора R равно ω = 3,44 σ0
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 811. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |

 или вероятности P(x), соответствующие каждому интервалу. На ширине каждого интервала строят прямоугольник, высота которого равна соответствующей частоте (частости, вероятности). В результате построения получается столбчатая ступенчатая диаграмма 1, называемая гистограммой распределения.
или вероятности P(x), соответствующие каждому интервалу. На ширине каждого интервала строят прямоугольник, высота которого равна соответствующей частоте (частости, вероятности). В результате построения получается столбчатая ступенчатая диаграмма 1, называемая гистограммой распределения.

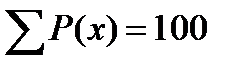 %
%
 Если в середине каждого интервала построить ординаты, соответствующие mi,
Если в середине каждого интервала построить ординаты, соответствующие mi, 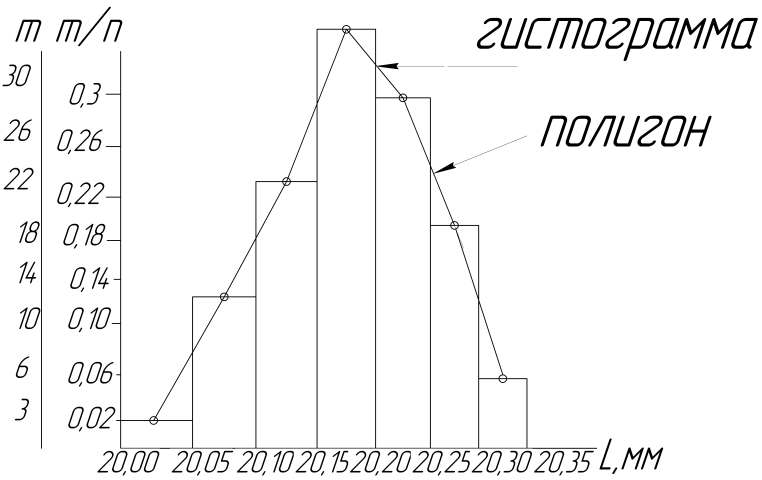
 (2.3)
(2.3)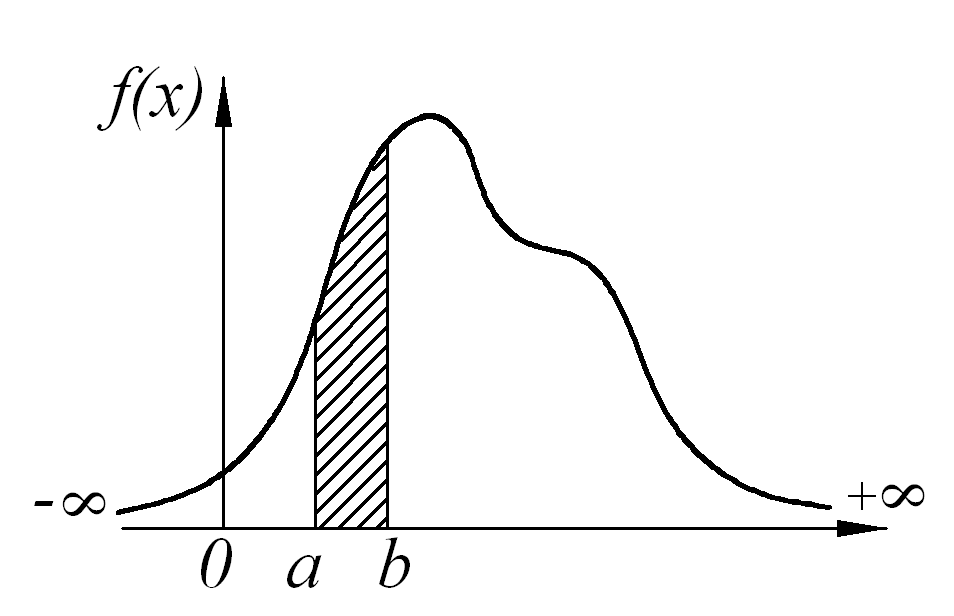
 (2.4)
(2.4) ,
, 
 (5)
(5)
 (2.7)
(2.7) .
.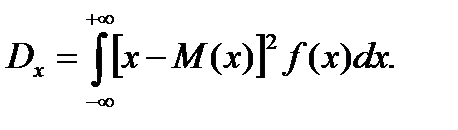 .
.
 (8)
(8) (2.9)
(2.9)



 (см.рис. 2.8.). Среднее значение случайной величины
(см.рис. 2.8.). Среднее значение случайной величины 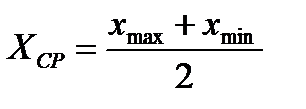 , среднее квадратическое отклонение
, среднее квадратическое отклонение  .
.

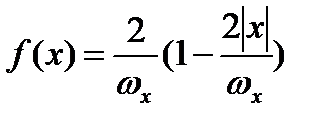 ,
, .
. . В таблице 2.3 приведены значения коэффициентов.
. В таблице 2.3 приведены значения коэффициентов.




 ,
,