
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Свойства умножения вектора на число.1) 2) 3) 4)
Доказательство 1). Пусть для простоты
Рис.1.3. Иллюстрация свойства сложения векторов Доказательство 2)–4). Очевидно с учетом того, что при этом получаются коллинеарные вектора.
Замечание. Можно определить операцию вычитания векторов по формуле  (см. рис.1.4) (см. рис.1.4)
Рис. 1.4. Вычитание векторов 2о. Линейно зависимые и линейно независимые системы векторов Определение 11.Линейной комбинацией векторов Определение 12.Вектора Определение 13.Вектора Теорема 1. 1) Для того, чтобы элементы 2) Если среди 3) Если часть элементов множества Доказательство. 1.
 2. Если 3. Если Теорема 2. Два вектора коллинеарны тогда и только тогда, когда они линейно зависимы. Доказательство. Если один из векторов нулевой, то очевидно. Поэтому далее предполагаем, что оба вектора ненулевые.
Следствие 1. Если Доказательство. Теорема 3. Три вектора компланарны тогда и только тогда, когда они линейно зависимы. Доказательство. Будем предполагать, что никакие два вектора из трех не коллинеарны, так как иначе утверждение очевидно в силу свойства линейно зависимых векторов.
Рис.1.5. Иллюстрация доказательства теоремы 3.
Теорема 4. Любые четыре вектора линейно зависимы. Доказательство. Предположим, что никакие три из векторов
Рис.1.6. Иллюстрация доказательства теоремы 4.
Определение 14.Базисом на прямой (соответственно, на плоскости и в пространстве) называется упорядоченный набор из одного (соответственно, из двух и трех) линейно независимых векторов. Замечание. Очевидно, что рассматриваемые векторы должны быть ненулевыми. Теорема 5(о существовании и единственности разложения по базису). Всякий вектор пространства (соответственно, плоскости и прямой) однозначно представляется в виде линейной комбинации векторов данного базиса. Доказательство. Докажем существование искомой линейной комбинации для пространства. Пусть векторы
Докажем единственность. От противного. Пусть имеется два различных набора чисел Определение 15.Координатами (компонентами) вектора
Также будем писать Теорема 6 (операции над векторами, заданными своими координатами). При сложении любых двух векторов Доказательство. Пусть
|
|||||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 179. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
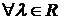 и
и 
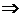
 .
. и
и  вектора
вектора 
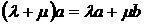 .
. .
. .
.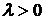 и будем использовать правило параллелограмма для сложения векторов. Если вместо
и будем использовать правило параллелограмма для сложения векторов. Если вместо 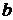 взять
взять  и
и 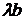 , то получим подобный параллелограмм и его диагональ соответственно равна
, то получим подобный параллелограмм и его диагональ соответственно равна  (см. рис.1.3).
(см. рис.1.3).
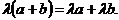

 с коэффициентами
с коэффициентами  R называется выражение вида:
R называется выражение вида:  .
. называются линейно зависимыми, если
называются линейно зависимыми, если  R, из которых хотя бы одно отлично от нуля, и линейная комбинация
R, из которых хотя бы одно отлично от нуля, и линейная комбинация  с этими
с этими  является нулевым вектором, т.е.
является нулевым вектором, т.е.  .
.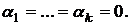

 Пусть векторы
Пусть векторы  – линейно зависимы, т.е.
– линейно зависимы, т.е.  и, например,
и, например,  . Тогда
. Тогда  и
и  , т.е.
, т.е.  является линейной комбинацией
является линейной комбинацией 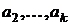 .
. Пусть
Пусть  . Тогда
. Тогда  , где
, где 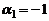 , т.е.
, т.е.  – линейно зависимы.
– линейно зависимы.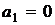
 и
и  – любое, например,
– любое, например, 
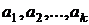 - линейно зависимы.
- линейно зависимы.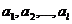 – линейно зависимы, то
– линейно зависимы, то  одновременно неравные нулю, так что
одновременно неравные нулю, так что 
 и хотя бы одно из
и хотя бы одно из 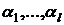 отлично от нуля
отлично от нуля  . Тогда если
. Тогда если  , то
, то 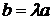 , если
, если  , то
, то  . В обоих случаях
. В обоих случаях  , где
, где  не равно 0. Тогда, если
не равно 0. Тогда, если  ,
, 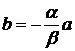
 , то
, то  R:
R:  R:
R: 

 . Т.о.
. Т.о. 
 .
. компланарны. Перенесем их в точку O, проведем через конец вектора c прямые, параллельные векторам
компланарны. Перенесем их в точку O, проведем через конец вектора c прямые, параллельные векторам  .(см. рис. 1.5) Векторы
.(см. рис. 1.5) Векторы  ,
,  – коллинеарны
– коллинеарны  R:
R:  ,
,  . Но
. Но 
 ,
, 
 R, одновременно не равные нулю:
R, одновременно не равные нулю:  . Если, например,
. Если, например,  , то
, то 
 не компланарны (иначе они линейно зависимы) очевидно. Остальное следует из (рис.1.6) по аналогии с доказательством теоремы 4. Через точку D проведем три плоскости, параллельные парам векторов {
не компланарны (иначе они линейно зависимы) очевидно. Остальное следует из (рис.1.6) по аналогии с доказательством теоремы 4. Через точку D проведем три плоскости, параллельные парам векторов { 
 ,
, 
 .
.  R:
R: 
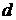 – линейно зависимы.∎
– линейно зависимы.∎ образуют данный базис, а
образуют данный базис, а  линейно зависимы, так что существует нетривиальная линейная комбинация
линейно зависимы, так что существует нетривиальная линейная комбинация  . Если
. Если  , то имеем
, то имеем 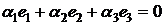 , причем одно из чисел
, причем одно из чисел  , что противоречит линейной независимости
, что противоречит линейной независимости  и искомая комбинация имеет вид
и искомая комбинация имеет вид .
. и
и  таких, что
таких, что  и
и 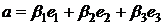 . Тогда
. Тогда  и в силу линейной независимости
и в силу линейной независимости  , что противоречит различию наборов чисел. ∎
, что противоречит различию наборов чисел. ∎
 на
на  , все координаты вектора умножаются на это число.
, все координаты вектора умножаются на это число. – базис,
– базис,  . Тогда в силу свойств операций сложения векторов и умножения вектора на число имеем
. Тогда в силу свойств операций сложения векторов и умножения вектора на число имеем ,
,  . В силу единственности разложения по базису
. В силу единственности разложения по базису