
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Построение функции Грина задачи. ⇐ ПредыдущаяСтр 2 из 2 Если задача (2.1) – (2.7) невырождена (т.е. имеет единственное решение) на Г, то ее решение для функции
Определение. Функцией Грина 1. при 2. при 3. при
(для уравнения порядка 4. при
(где
Функцию Грина задачи (2.1) - (2.7) на графе
где
Положим в задаче (2.1) - (2.7) Функцию
где
Согласно определению функции Грина на отрезке, она должна удовлетворять однородному уравнению, поэтому найдем фундаментальную систему решений однородного уравнения По левым частям краевых условий (2.16) построим функционалы: Так как функция Грина должна удовлетворять краевым условиям, то 
Функцию Грина задачи (4.5) будем искать в виде:
где по равенствам (4.6) можно найти функция
Итак
Построим
Аналогично строим
Построим
Тогда функция Грина задачи (2.1) - (2.7) определяемая по формуле (4.2), имеет вид:
где
H(x,s) определяется по формуле (4.4).
5. Решение дифференциального неравенства
Рассмотрим задачу (2.1)-(2.7).
Теорема 3. Если Доказательство. Возможны 3 случая: 1) Рассмотрим 1-ый случай: Если Из условия непрерывности (2.3) имеем: Из условия непрерывности (2.4) имеем: Рассмотрим случай 1.2: Функция Из условия непрерывности (2.3) имеем: Из условия непрерывности (2.4) имеем: Рассмотрим случай 1.3: Функция Рассмотрим 2-ой случай: Пусть теперь Рассмотрим случай 2.1: Если
Так как Рассмотрим случай 2.2: Если функция
Так как Рассмотрим случай 2.3: Если функция
Так как Рассмотрим 3-ий случай: Заметим, что если поменять направление на каждом из
Следствие: Если
ЛИТЕРАТУРА
1. Эльсгольц Л.Э. Дифференциальные уравнения и вариационное исчисление Серия: «Курс высшей математики и математической физики» -3выпуск/Главная редакция физико-математической литературы. М.: Наука,1969.-424с.
2. Камке Э. Справочник по обыкновенным дифференциальным уравнениям. – М.: Физматлит, 1961.
3. Петровский И.Г. Лекции по теории обыкновенных дифференциальных уравнений/ Под ред. И.Е. Морозова – М. :Наука, 1964.- 272с.
4. Покорный Ю.В. Дифференциальные уравнения на геометрических графах/Ю.В. Покорный, О.М. Пенкин, В.Л. Прядиев, А.В. Боровских. К.П. Лазарев, С.А. Шабров М. : Физматлит, 2004.- 272с. |
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 243. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 , и любой
, и любой  может быть представлено в виде:
может быть представлено в виде: . (4.1)
. (4.1)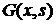 на отрезке называют функцию двух переменных
на отрезке называют функцию двух переменных  и
и 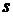 , при каждом фиксированном
, при каждом фиксированном 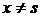
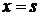 непрерывна по
непрерывна по 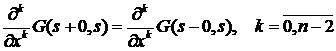 ,
,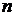 )
) ,
,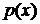 - коэффициент при старшей производной дифференциального уравнения порядка
- коэффициент при старшей производной дифференциального уравнения порядка 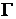 можно построить по формуле:
можно построить по формуле: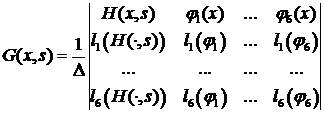 (4.2)
(4.2)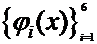 - фундаментальная система решений однородного уравнения
- фундаментальная система решений однородного уравнения 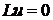 .
. (4.3)
(4.3)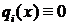 .
.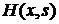 можно построить по функциям Грина двухточечных задач (задач на отрезках) на
можно построить по функциям Грина двухточечных задач (задач на отрезках) на  :
: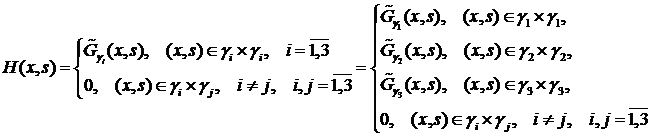 (4.4)
(4.4)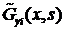 - функция Грина двухточечной краевой задачи на отрезке
- функция Грина двухточечной краевой задачи на отрезке  :
: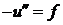 на
на  , (4.5)
, (4.5)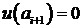 ,
,  , (
, (  )
)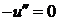 :
: 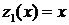 ,
, 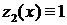 .
.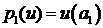 ,
, 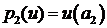 .
.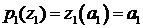 ,
, 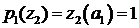
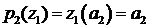 ,
, 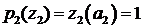 . (4.6)
. (4.6)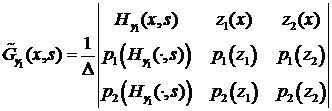 ,
,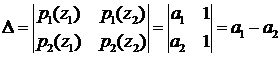 ,
, - какое-либо решение неоднородного уравнения задачи (4.5), которое может быть найдено, например, с помощью функции Коши:
- какое-либо решение неоднородного уравнения задачи (4.5), которое может быть найдено, например, с помощью функции Коши: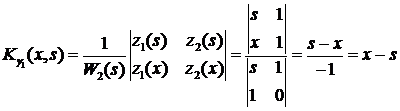 .
.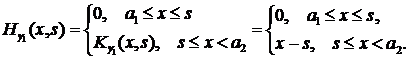
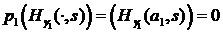 ,
, 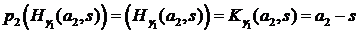 .
.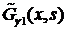 на
на 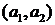 :
: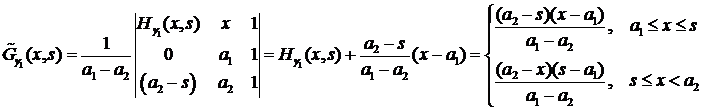
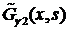 и
и 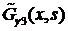 :
: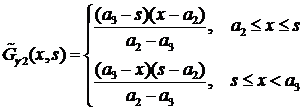 ,
, 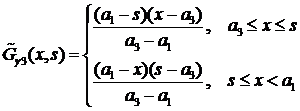
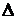 по формуле (4.3):
по формуле (4.3):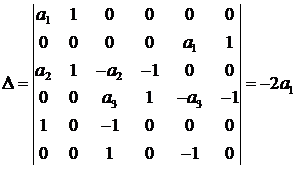 ,
,
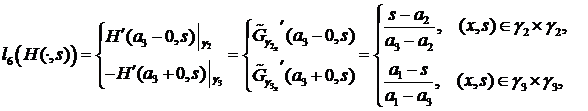
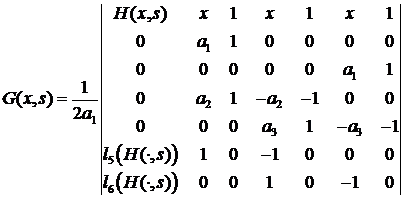 ,
,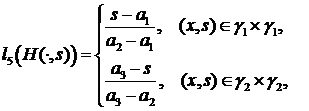 ,
, 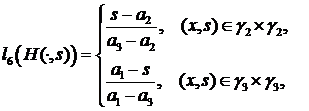
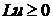 .
.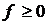 на Г, то
на Г, то  на Г.
на Г.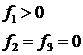 ; 2)
; 2) 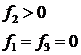 ; 3)
; 3)  .
.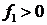 ,
, 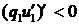 и функция
и функция 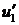 убывает на
убывает на 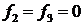 , то
, то  ,
, 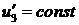 . Пусть
. Пусть 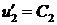 ,
, 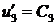 . Функция
. Функция 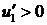 ; 1.2
; 1.2 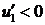 ; 1.3
; 1.3 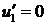 . Рассмотрим случай 1.1: Если
. Рассмотрим случай 1.1: Если  . Тогда, учитывая условие (2.1):
. Тогда, учитывая условие (2.1):  ,
,  возрастает от точки
возрастает от точки  до
до  и, имеем
и, имеем 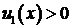 на
на  и условия баланса (2.5) имеем:
и условия баланса (2.5) имеем: 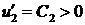 , следовательно, функция
, следовательно, функция  возрастает от точки
возрастает от точки  . Тогда
. Тогда 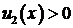 на
на  .
. и условия баланса (2.6) имеем:
и условия баланса (2.6) имеем: 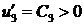 , следовательно, функция
, следовательно, функция  возрастает от точки
возрастает от точки  на
на  .
. на
на 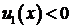 на
на 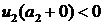 и условия баланса (2.5) имеем:
и условия баланса (2.5) имеем: 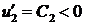 , следовательно, функция
, следовательно, функция 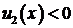 на
на 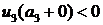 и условия баланса (2.6) имеем:
и условия баланса (2.6) имеем: 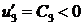 , следовательно, функция
, следовательно, функция 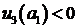 на
на 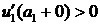 ,
, 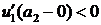 . Так как
. Так как 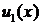 возрастает от точки
возрастает от точки 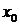 . Так как
. Так как 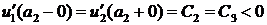 , из условия непрерывности
, из условия непрерывности 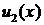 убывает от точки
убывает от точки  убывает от точки
убывает от точки 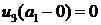 , следует, что
, следует, что  внутри
внутри  и
и 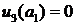 . Следовательно функция
. Следовательно функция  на Г, и
на Г, и 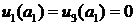 на
на 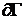 .
.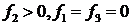 . Если
. Если 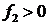 ,
, 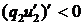 и функция
и функция 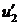 убывает на
убывает на 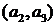 . Так как
. Так как 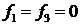 , то
, то 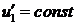 ,
,  ,
, 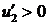 ; 2.2
; 2.2 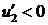 ; 2.3
; 2.3 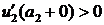 и
и 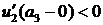 .
. и
и 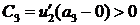 . Так как
. Так как 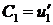 на
на 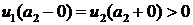 .
. на
на 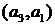 и
и  , то
, то  на
на 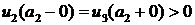 , следует, что
, следует, что 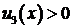 на
на 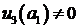 , противоречит условию (2.2).
, противоречит условию (2.2).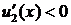 на
на  и
и 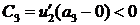 . Так как
. Так как 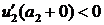 , то
, то 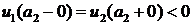 .
.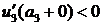 , то
, то 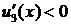 на
на 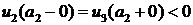 , следует, что
, следует, что 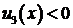 на
на  возрастает от точки
возрастает от точки  на
на