
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Основные понятия теории краевых задач на графахСтр 1 из 2Следующая ⇒ ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ “ВОРОНЕЖСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ” Математический факультет
Кафедра функционального анализа и операторных уравнений
ИССЛЕДОВАНИЕ ОДНОЙ КРАЕВОЙ ЗАДАЧИ НА ГРАФЕ ДЛЯ СТРУННОЙ СИСТЕМЫ С ЦИКЛОМ ВЫПУСКНАЯ КВАЛИФИКАЦИОННАЯ РАБОТА Специальность – 010101 Математика 010109 – Функциональный анализ
Допущено к защите в ГАК
Воронеж2009 Оглавление Введение…………………….……………………………….………..стр.2
1. Основные понятия теории краевых задач на графах………………………………………………...…......……….стр.3
2. Постановка краевой задачи…………………….………………стр.6
3. Невырожденность………………………..……..………………стр.9
4. Построение функции Грина задачи………………...…………стр.12
5. Решение дифференциального неравенства…………...............стр.16
Введение Дипломная работа посвящена актуальной в последнее время теории дифференциальных уравнений на графах, в частности графах с циклом. Изучаемый граф интересен тем, что, имея ясную физическую природу, он содержит главные особенности, порождающие дополнительны проблемы в задачах на графах, а именно: сложные стыковки и наличие цикла. В первой части работы приводятся основные понятия теории дифференциальных уравнений на графах [1], [2],[3]. Во второй части работы дано подробное описание модели «треугольник из струн» и по классической вариационной схеме Лагранжа [4] построена неоднородная краевая задача для исследуемой модели.  Используя классические методы теории обыкновенных дифференциальных уравнений на отрезке и качественные методы задачи Штурма-Лиувилля [4] на графе для построенной неоднородной задачи для изучаемой модели, в третьей части исследована соответствующая однородная задача. Получено условие невырожденности построенной неоднородной задачи. В четвертой части построена функции Грина, позволяющая представить решение исследуемой задачи в интегральном виде. В пятой заключительной части работы было исследовано дифференциальное неравенство Основные понятия теории краевых задач на графах
Напомним основные определения из теории краевых задач на графах. Геометрическим графом Будем говорить, что вершины Будем рассматривать вещественнозначные функции Для каждого ребра Если рассматривать замкнутые ребра Производная на графе определяется следующим образом. Если для данной параметризации Через Будем писать Введем пространства: Основным объектом исследований является следующая краевая задача на графе
Решением задачи назовем функцию При исследовании разрешимости задачи будем рассматривать однородную задачу:
Постановка краевой задачи. Рассмотрим струнную систему,
состоящую из трех струн, образующих треугольник, одна вершина которого закреплена:
а к двум другим вершинам прикреплены колечки, одетые на спицы:
Обозначим всю геометрическую систему через Будем считать, что на систему действует сила с плотностью характеризуют упругость струн. Будем считать, что смещение точек механической системы от положения равновесия происходит параллельно некоторой прямой под действием внешней нагрузки, направленной вдоль этой прямой. Общая потенциальная энергия системы, соответствующая возможной деформации
Согласно вариационному принципу: «Реальная деформация системы, отвечающая устойчивому равновесию, должна давать минимум потенциальной энергии».
Теорема 1. Пусть потенциальная энергия рассматриваемой системы определяется функционалом (2.8), тогда для
и условиям
Доказательство. Пусть тогда Найдем: После интегрирования по частям
получим:
Выбирая
Если Пусть условие (2.5) выполнено для любого h, тогда из уравнения (2.9’), учитывая условия непрерывности (2.4) получаем условие (2.6).
Таким образом, на Г построена неоднородная задача:
Соответствующая ей однородная задача имеет вид:
Невырожденность.
Рассмотрим неоднородную задачу (2.1) – (2.7). По левым частям равенств (2.1) – (2.6) построим функционалы
По левой части равенства (2.7) построим дифференциальный оператор:
Тогда неоднородная задача (2.1) – (2.7) сводится к задаче:
А однородная задача (2.1) – (2.7’) к задаче:
Теорема 2.(Условие невырождености). Задача (3.1) для Доказательство. Так как В частности на Возможны 3 случая: 1) Если Из Из условия непрерывности (2.3) имеем: Из условия (2.5) получим,
Из Из условия (2.6) получим:
Из 2) Аналогично, при 3) Если Из Из условия непрерывности (2.3) и условия (2.5), имеем:
Тогда Из равенства (2.6) имеем,
Тогда
Итак, из трех рассмотренных случаев возможен только один: Итак, |
||||||||||||||||||||||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 200. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
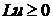 . Было установлено, что при неотрицательной правой части неоднородной задачи, ее решение неотрицательно.
. Было установлено, что при неотрицательной правой части неоднородной задачи, ее решение неотрицательно. в
в  называется объединение непересекающихся интервалов
называется объединение непересекающихся интервалов  =
= 
 ,
,  (называемых ребрами), и некоторой совокупности их концов. Множество этих концов обозначается через
(называемых ребрами), и некоторой совокупности их концов. Множество этих концов обозначается через  , каждая точка из
, каждая точка из  .Обозначим множество всех вершин графа
.Обозначим множество всех вершин графа  , и объединение всех ребер -
, и объединение всех ребер -  . Тогда
. Тогда  .
. и c примыкают к ребру
и c примыкают к ребру  , а ребро
, а ребро  . Для каждой вершины
. Для каждой вершины  введем множество
введем множество  , состоящее из
, состоящее из  и всех ребер, примыкающих к
и всех ребер, примыкающих к  , сужение которых на ребро
, сужение которых на ребро  .
. , где
, где  и
и  - длина ребра
- длина ребра  оказывается обычной функцией на промежутке из
оказывается обычной функцией на промежутке из  .
. , то считать его параметризацией
, то считать его параметризацией  .
. ребра
ребра 
 при всех
при всех  и
и  существует производная
существует производная 
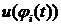 , то будем говорить, что на
, то будем говорить, что на  . При этом на ребре
. При этом на ребре  , если
, если  имеем набор производных
имеем набор производных 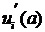 для ребер
для ребер  . Заметим, что на каждом ребре можно ввести две натуральных параметризации с противоположной ориентацией, и, естественно, производные первого порядка зависят от ориентации ребра, а производные второго порядка – нет. При формулировании условий согласования, нам удобнее пользоваться производными по направлению “от вершины”, которые будем обозначать
. Заметим, что на каждом ребре можно ввести две натуральных параметризации с противоположной ориентацией, и, естественно, производные первого порядка зависят от ориентации ребра, а производные второго порядка – нет. При формулировании условий согласования, нам удобнее пользоваться производными по направлению “от вершины”, которые будем обозначать  .
. обозначим множество, определенных на ребре
обозначим множество, определенных на ребре  можно доопределить предельными значениями до функции из
можно доопределить предельными значениями до функции из  , за доопределенной функцией сохраним прежнее обозначение.
, за доопределенной функцией сохраним прежнее обозначение. , если
, если  и сужения
и сужения  . Во внутренних вершинах графа Г каждая из таких функций может иметь различные пределы вдоль различных ребер, примыкающих к одной вершине
. Во внутренних вершинах графа Г каждая из таких функций может иметь различные пределы вдоль различных ребер, примыкающих к одной вершине  . Если все пределы
. Если все пределы  вдоль ребер
вдоль ребер  совпадают, то для них будем использовать обозначение
совпадают, то для них будем использовать обозначение  .
. .
. (1.1.)
(1.1.)
 (1.2.)
(1.2.)
 ,
,  . (1.4.)
. (1.4.) , удовлетворяющую уравнению (1.1.) на
, удовлетворяющую уравнению (1.1.) на  (1.5.)
(1.5.)
 , (2.1)
, (2.1) , (2.2)
, (2.2) , (2.3)
, (2.3) (2.4)
(2.4) . Рассмотрим на Г скалярную функцию
. Рассмотрим на Г скалярную функцию  такую, что
такую, что  . Сужение функции
. Сужение функции  на
на  ,
,  , и
, и  обозначим
обозначим  ,
, 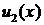 и
и  соответственно.
соответственно. . Функции
. Функции  и
и  ,
, 

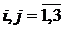
 . (2.8)
. (2.8) функционала (2.8) удовлетворяет уравнениям:
функционала (2.8) удовлетворяет уравнениям: , (2.7)
, (2.7) . (2.5)
. (2.5) . (2.6)
. (2.6) min =
min =  ,
,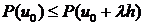 ,
,  , и удовлетворяет условиям (2.1) - (2.4)
, и удовлетворяет условиям (2.1) - (2.4)
 ,
, (2.9)
(2.9) ,
,  ) получаем уравнение Эйлера:
) получаем уравнение Эйлера: на
на  (2.9’)
(2.9’) в остальных случаях, тогда получаем
в остальных случаях, тогда получаем  , т.е. (2.5)
, т.е. (2.5) (2.7’)
(2.7’) ,
, 




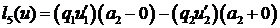


 ,
,  . (3.1)
. (3.1) ,
,  на
на  ,
, 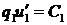
 ,
,  ,
,  .
. следует, что функция
следует, что функция  возрастает от точки
возрастает от точки  до
до  , и так как
, и так как  на
на  .
. .
. =
=  , что равносильно равенству:
, что равносильно равенству: 
 следует, что функция
следует, что функция  возрастает от точки
возрастает от точки  , и так как
, и так как  на
на  , что из условия непрерывности (4) имеем:
, что из условия непрерывности (4) имеем:  .
. =
=  , что равносильно равенству:
, что равносильно равенству:  .
. следует, что функция
следует, что функция  возрастает от точки
возрастает от точки  на
на  , что противоречит (2.2). Следовательно случай
, что противоречит (2.2). Следовательно случай  следует, что функция
следует, что функция  , и так как
, и так как  на
на  .
. .
. , и
, и  ,а это означает, что
,а это означает, что  на
на  , что по условию непрерывности (2.4) означает:
, что по условию непрерывности (2.4) означает:  .
. .
. , и
, и  ,а это означает, что
,а это означает, что  на
на  на
на  на Г.
на Г.