
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
П2.1 Основные уравнения динамики ⇐ ПредыдущаяСтр 4 из 4 Одномерных стационарных течений К одномерным течениям относят такое движение жидкости, когда продольные размеры потока во много раз превосходят поперечные, например, в трубах, каналах, реках и т.д. В качестве характеристик поперечного сечения потока применяют: · площадь сечения S; · среднюю скорость в сечении
где u – скорость в данной точке сечения; · массовый и объемный секундные расходы
· смоченный периметр χ– длина соприкасающейся с жидкостью дуги границы нормального сечения трубы или канала; · гидравлический диаметр DГ– отношение учетверенной площади нормального сечения к смоченному периметру:
Иногда в качестве характеристики используется гидравлический радиус:
При одномерном установившемся движении основные уравнения гидродинамики могут быть существенно упрощены. Уравнение неразрывности вырождается в уравнение постоянства расхода:
Илиприρ= const:v1S1 = v2S2. Здесь v1и v2 – модули средних скоростей в сечениях (рис. П2.1).
Рис. П2.1
Уравнение количества движения принимает вид формулы Эйлера
где Уравнение кинетической энергии записывается в виде уравнения Бернулли для реальных потоков
Все члены этого уравнения имеют размерность длины и их в гидромеханике именуют высотами или напорами: z – нивелировочная высота или просто высота;
Коэффициент α(коэффициент Кориолиса) представляет собой отношение действительной кинетической энергии к кинетической энергии, подсчитанной по средней скорости. Для равномерных течений α= 1. 
Dh12– удельная мощность внутренних сил на участке 1–2, или потеря полного напора (гидравлические потери). Для идеальной жидкости уравнение Бернулли примет вид:
где H – гидравлическая или полная высота;
В единицах давления уравнение Бернулли принимает вид:
Здесь p – статическое давление; ρgz – весовое давление;
Линия, характеризующая изменение пьезометрического напора вдоль течения называется пьезометрической линией. Ее уклон называется пьезометрическим уклоном:
Здесь l – длина. Линия, проведенная по отметкам гидродинамических напоров, называется напорной линией (линией энергий), а ее уклон:
называется гидравлическим уклоном. Принято считать пьезометрический и гидравлический уклоны положительными, если они направлены в сторону движения жидкости (рис.П2.2). Гидравлический уклон мыслим только в вязкой жидкости. Он всегда направлен в сторону движения жидкости. Пьезометрический уклон может быть направлен как в сторону движения, так и в противоположную сторону.
Рис. П2.2
П2.2 Гидравлические потери Все потери при одномерном течении принято разделять на потери по длине и местные потери. Иначе, потери полного напора называют гидравлическими сопротивлениями. Природа гидравлических сопротивлений достаточно сложна. Они зависят от сил внутреннего и внешнего трения, а также от геометрии твердых границ. Их теоретическое исследование слишком сложно и поэтому на практике пользуются экспериментальным изучением. Гидравлические потери самым существенным образом зависят от режима течения жидкости. Можно выделить два режима движения жидкости: ламинарный, при котором частицы жидкости движутся слоями, без перемешивания, и турбулентный, с беспорядочным перемешиванием. Переход от ламинарного к турбулентному режиму происходит при некотором критическом числе Рейнольдса.
где v – средняя скорость, d – характерный размер (гидравлический диаметр сечения), μ – коэффициент динамической вязкости. Размерность коэффициента вязкости динамического [μ] = Н с/м2, кинематического [ν] = [μ/ρ] = м2/c. Обратный переход от турбулентного режима к ламинарному произойдет при гораздо меньшем числе Рейнольдса. Экспериментально установлены верхнее и нижнее числа Рейнольдса
Потери напора по длинекруглого трубопровода могут быть найдены по формуле Дарси - Вейсбаха
где Коэффициент гидравлического трения при Re<2300 (ламинарный режим) может быть подсчитан по формуле Пуазейля
При Re>2300 (турбулентный режим) – по формуле Альтшуля
Здесь δ – средняя шероховатость (высота бугорков стенок) трубы (мм). При расчетах можно брать значенияδиз таблицы П2.1. В единицах давления запишем
В области переходного режима (2300 <Re<10d /δ) для гладких труб имеем формулу Блазиуса:
Потери напора на местных сопротивленияхнаходятся по формуле Вейсбаха
где ξМ– коэффициент местных потерь напора, v – средняя скорость за сопротивлением (кроме случая резкого расширения). В единицах давления – Для некоторых местных сопротивлений коэффициенты потерь приведены в таблице П2.2. Таблица П2.1
Таблица П2.2
Таблица П2.3
Приложение 3. Истечение жидкости из отверстий и насадков В гидравлике различают большие и малые отверстия. Отверстие называют малым, если его вертикальный размер не превышает 0,1 напора. При истечении из малого отверстия в тонкой стенке при постоянном напоре (рис.П3.1) скорость v и расход Q жидкости определяются по формулам:
S – площадь отверстия; H – геометрический напор над центром тяжести отверстия; p1– давление на свободной поверхности жидкости; p2– давление в среде, в которую происходит истечение. Коэффициенты φ и μ связаны между собой соотношением μ= ε·φ, (П3.3) где ε – коэффициент сжатия струи, представляющий собой отношение площади струив сжатом сечении к площади Рис.П3.1 отверстия.
Коэффициент скорости φ находится через коэффициент ξ потерь местного сопротивления и коэффициент α кинетической энергии по формуле
При истечении жидкости из открытого резервуара в атмосферу (p1= p2= pа) формулы (П3.1) и (П3.2) принимают простой вид:
Таблица П3.1
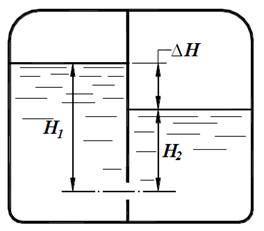
При истечении под уровень (в этом случае отверстие называется затопленным) скорость и расход (рис.П3.2) находятся по формулам:
Рис. П3.2где ΔH – разность уровней.
Если резервуары являются открытыми (p1 = p2 = pa), то формулы (3.7) и (3.8) упрощаются:
Насадкомназывается короткая трубка (длиной 3–4 диаметра), прикрепленная к отверстию. В зависимости от формы насадки делятся на цилиндрические (внешние и внутренние (рис.П3.4а,б)) и конические (сходящиеся и расходящиеся (рис.П3.4в,г)).
а) б) в) г) Рис. П3.2
Скорость и расход при истечении из насадка определяются по тем же формулам, что и при истечении через малое отверстие. Значения коэффициентов сжатия струи ε, скорости φи расходаμ приведены в таблице П3.2. Таблица П3.2
|
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 914. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |


 .
.



 -сумма внешних сил, объемных и поверхностных, действующих на выделенный сечениями 1 и 2 объем жидкости.
-сумма внешних сил, объемных и поверхностных, действующих на выделенный сечениями 1 и 2 объем жидкости.
 – скоростная высота.
– скоростная высота.  – пьезометрическая высота.
– пьезометрическая высота. 
 – потенциальный или пьезометрический напор;
– потенциальный или пьезометрический напор; – скоростной (кинетический) напор.
– скоростной (кинетический) напор. 
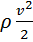 – – кинетическое давление.
– – кинетическое давление.
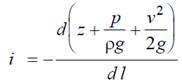

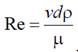


 – коэффициент потерь по длине,λ – коэффициент гидравлического трения (коэффициент Дарси); v – средняя скорость.
– коэффициент потерь по длине,λ – коэффициент гидравлического трения (коэффициент Дарси); v – средняя скорость.




 .
.




 (П3.1)
(П3.1) (П3.2)
(П3.2)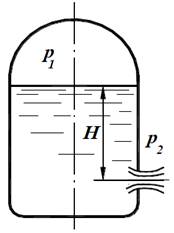 где φ, μ – коэффициенты скорости и расхода, значения которых приведены в таблице П3.1;
где φ, μ – коэффициенты скорости и расхода, значения которых приведены в таблице П3.1; (П3.4)
(П3.4) (П3.5)
(П3.5) (П3.6)
(П3.6)
 (П3.7)
(П3.7) (П3.8)
(П3.8) (П3.7)
(П3.7) (П3.8)
(П3.8)
