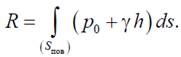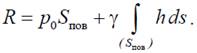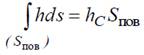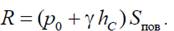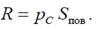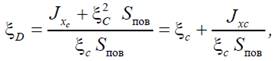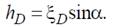Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Методические указания к решению задачи 2При решении задач динамики реальной жидкости необходимо использовать уравнение Бернулли и уравнение постоянства расхода. Коэффициент Кориолиса α при решении задачи принять равным единице. С помощью уравнения постоянства расхода определяются скорости на отдельных участках трубопровода и подсчитываются числа Рейнольдса, Re. После этого можно найти гидравлические потери на отдельных участках трубопровода и местных сопротивлениях. При определении гидравлических потерь рекомендуется пользоваться зависимостями, приведенными вПриложенииП2. Затем можно определить скоростные напоры на отдельных участках трубопровода. После этого строятся графики, полного скоростного и пьезометрического напоров.
Контрольные вопросы 1. Что такое расход жидкости? 2. В каких единицах измеряется расход жидкости? 3. Как записывается уравнение неразрывности? 4. Какой физический закон выражает уравнение неразрывности? 5. Как записывается уравнение Бернулли для потока идеальной жидкости? 6. В чем смысл коэффициента Кориолиса? 7. Какой физический закон выражает уравнение Бернулли? 8. Каков энергетический смысл членов уравнения Бернулли? 9. Что такое пьезометрическая и напорная линии? 10. Что такое пьезометрический и гидравлический уклоны? 11. Как записывается уравнение Бернулли для потока реальной жидкости? 12. В чем энергетический смысл членов уравнения Бернулли для потока реальной жидкости? 13. Чем отличается ламинарный режим от турбулентного? 14. Как выглядит поле скоростей в канале при ламинарном течении? 15. Как выглядит поле скоростей в канале при турбулентном течении?  16. Как можно найти касательные напряжения при течении жидкости в канале? 17. Как записывается формула Дарси - Вейсбаха? 18. Что такое коэффициент гидравлического трения? 19. Как выглядит кривая Никурадзе? 20. Какие области можно выделить на кривой Никурадзе? 21. Что характеризует собой число Рейнольдса? 22. Как записывается формула Пуазейля? 23. Как записывается формула Блазиуса? 24. Как записывается формула Альтшуля? 25. Что такое область квадратичного сопротивления? 26. Что такое область линейного сопротивления? 27. Какие гидравлические потери называются местными? 28. Могут ли оставаться постоянными (увеличиваться, уменьшаться) вдоль потока пьезометрический и гидравлический напоры вязкой жидкости?
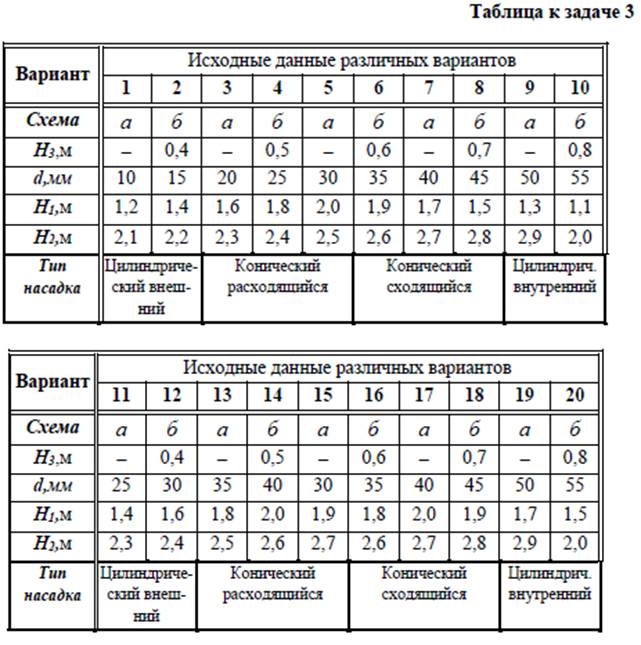
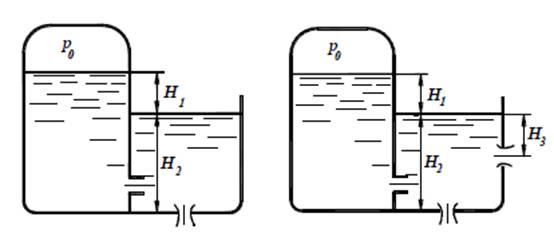
Задача 3.Истечение жидкости из отверстий и насадков Истечение воды из закрытого резервуара происходит через насадок, а из открытого – через отверстие в тонкой стенке. Диаметры выходного отверстия насадка и отверстия в тонкой стенке одинаковы. Определить расход воды через систему и избыточное давление p0 в закрытом резервуаре.
схемаасхема б
Методические указания к решению задачи 3 Для решения задачи следует воспользоваться зависимостями П3.7 и П3.8 (см. Приложение 3). Коэффициенты расхода при истечении через насадки можно брать по таблице П3.2.
Контрольные вопросы 1. Какое отверстие считается малым? 2. Когда можно говорить об истечении через отверстие в тонкой стенке? 3. Как записываются формулы для скорости и расхода при истечении жидкости через отверстия и насадки? 4. Какими коэффициентами характеризуются эти истечения? 5. Что характеризует коэффициент скорости? 6. Что характеризует коэффициент сжатия? 7. Что характеризует коэффициент расхода? 8. Какие известны виды насадков. 9. Почему пропускная способность насадка больше пропускной способности отверстия равного с ним сечения? 10. Как связаны между собой коэффициент сопротивления насадка и коэффициент расхода? 11. Как вычисляется расход жидкости при истечении через большое отверстие? 12. Чем отличаются формулы вычисления расхода жидкости для незатопленного и затопленного отверстий? 13. Как находится время опорожнения призматического резервуара через от верстие в тонкой стенке?
Приложение 1. Гидростатика В гидростатике изучаются законы равновесия жидкости и газа и их взаимодействие в этом состоянии с твердыми телами. Силы, действующие в сплошной среде, будут распределенными по объему или по поверхности. Массовыми (или объемными) силами будут силы тяжести и переносные силы инерции при равновесии в движущемся с ускорением сосуде. Интенсивность массовых сил
где Поверхностные силы в покоящейся жидкости направлены по нормали к рассматриваемой площадке. Интенсивность поверхностных сил
где Давление представляет собой физический скаляр. Единица гидростатического давления паскаль: 1Па =1Н/м2. В технике пользуются такой единицей как атмосфера: 1атм = 98066,5 Па ≈ 100 кПа = 0,1мПа, а также миллиметр ртутного столба: 1мм.рт.ст. =98066,5 Па/760 = 129 Па. При рассмотрении равновесия в покоящейся жидкости, направив ось Оzвертикально вверх, получим
или при ρ = const,
Величина H называется гидростатическим напором. С учетом ρg = γ – удельный вес, (П1.1) запишем в виде
Разность z0–z = h – глубина погружения. Теперь можем записать основную формулу гидростатики
Главный вектор сил давления жидкости на некоторую плоскую поверхность может быть найден как поверхностная сила:
Эта сила направлена по нормали от жидкости к поверхности. Интегрируя получим при γ = const:
Величина
– статический момент площадки относительно свободной поверхности жидкости; hC– заглубление центра тяжести площадки. Теперь
С учетом того, что (p0+γhС) = pC– давление в центре тяжести площадки, получим
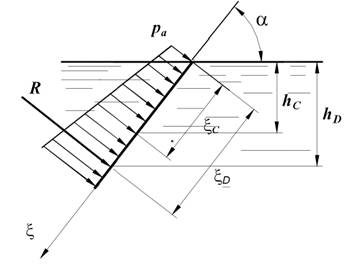
Точка приложения равнодействующей сил избыточного давления жидкости на площадку называется центром давления. Для плоской площадки силы давления параллельны между собой и центр давления найдется как центр параллельных сил (рис. П1.1). Координата ξDцентра давления жидкости на площадку может быть записана в виде
где Jxс– момент инерции площадки относительно ее центральной оси, параллельной линии пересечения свободной поверхности и плоскости в которой лежит площадка. Заглубление центра давления
Отсюда видно, что центр давления лежит ниже центра тяжести площадки.
Рис. П1.1
Приложение 2. Динамика одномерных течений Жидкости и газа |
||
|
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 291. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
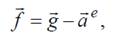
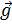–ускорение свободного падения; 
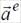–переносное ускорение частицы жидкости в движущемся сосуде.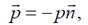
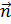– единичный вектор внешней нормали к площадке; p – гидростатическое давление, оно считается положительным, если является сжимающим для площадки.
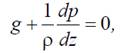(П1.1)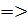
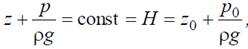
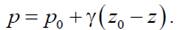(П1.2)
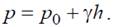(П1.3)
