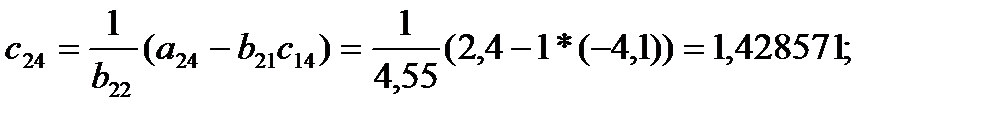Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Схема Гаусса с выбором главного элементаРассмотрим линейную систему уравнений:
Запишем расширенную матрицу коэффициентов системы: M= Среди элементов матрицы aij (i, j=1,...,n) выберем наибольший по модулю, называемый главным элементом. Пусть им будет, например, элемент apq. Строка с номером p, содержащая главный элемент, называется главной строкой. Далее вычисляем множители mi=aiq/apq для всех i Над матрицей M1, повторяем те же операции, после чего получим матрицу M2,и т. д. Такие преобразования продолжаем до тех пор, пока не получим матрицу, содержащую одну строку из двух элементов, которую считаем тоже главной. Затем объединяем все главные строки, начиная с последней. После некоторой перестановки они образуют треугольную матрицу, эквивалентную исходной. На этом заканчивается этап вычислений, называемый прямым ходом. Решив систему с полученной треугольной матрицей коэффициентов, найдем последовательно значения неизвестных xi (i=1,2, ...,n). Этот этап вычислений называется обратным ходом. Все описанные вычисления можно расположить в одной таблице, аналогично компактной схеме Гаусса, и на каждом этапе проводить рассмотренный выше контроль вычислений. Смысл выбора главного элемента состоит в том, чтобы сделать возможно меньшими числа mi и тем самым уменьшить погрешность вычислений. Поэтому при реализации метода Гаусса на ЭВМ обычно используют схему с выбором главного элемента.  Результаты всех вычислений удобно записывать в таблицу. Прямой ход: 1) Записываем в первом разделе таблицы коэффициенты системы aij (i=1,2,3,4; j=1,2,3,4,5). 2) В столбце å= ai6 записываем суммы коэффициентов по каждой строке. 3) Находим главный элемент, подчёркиваем его. 4) Находим числа mi по формуле mi= aiq/apq, где apq – главный элемент и результаты записываем в столбце mi раздела I. 5) Из каждой i–ой строки вычитаем главную строку, умноженную на соответствующий элемент mi. 6) Контроль: находим суммы
Решим с помощью данного метода ту же самую систему уравнений: Результаты всех вычислений будем записывать в таблицу (табл. 5): Прямой ход: 1) Записываем в первом разделе таблицы коэффициенты системы aij (i=1,2,3,4; j=1,2,3,4,5). 2) В столбце å= ai6 записываем суммы коэффициентов по каждой строке. 3) Находим главный элемент. В данной системе им будет коэффициент a14= -8,2 (p=1, q=4), выделяем этот элемент. 4) Находим числа mi (i=2,3,4). Для этого делим элементы столбца ai4 на a14 и результаты записываем в столбце mi разделаI: m2= 5) Вычисляем коэффициенты новой матрицы. Из каждой i–ой (i=2,3,4) строки вычитаем главную строку, умноженную на соответствующий элемент mi. Так, при i=2 будем иметь:
При i=3,4 продолжаем вычисления аналогичным образом. Результаты записываем в разделе II. При этом не выписываем главную строку. 6) Контроль: находим суммы 7) Выбираем главный элемент, выделяем его. В нашем случае это будет 8) Делим элементы столбца ai2 на
9) Вычисляем коэффициенты
=3,0045977;
=5,8041379;
=4,0974713;
=12,9062069. При i=3 вычисления ведутся аналогично. Результаты записываем в разделе III, оставляя свободными уже столбцы ai2 и ai4. 10) Контроль: сумма 11) Выбираем главный элемент, выделяем его. В нашем случае это будет 12) Находим 13) Вычисляем коэффициенты
=4,1734273;
=20,3273862; Таблица 5
=24,5008135. 14) Контроль: 15) Выписываем главные строки каждого раздела. Получим систему, эквивалентную данной системе: Обратный ход: 16) Результаты вычислений при реализации обратного хода записываем в разделе V: x1=20,3273862/4,1734273= 4,8706698, x3=(4,0974713 – 3,0045977*4,8706698)/ 5,8041379= -1,8154172, x2=(10,2304878 – 5,5121951*4,8706698 – 5,4914634*(-1,8154172))/ / (-6,8963415)= 0,9640325, x4=(0,9 – 2*4,8706698+3,5*0,9640325 – 2,7*(-1,8154172))/( -8,2)=0,0689755. Схема Халецкого Рассмотрим систему линейных уравнений, записанную в матричном виде: Ax=b, где A=(aij) – квадратная матрица (i, j=1,2,...,n) и x= b= Тогда элементы bij и cij будут определяться по формулам:
Отсюда искомый вектор x может быть вычислен из цепи уравнений By=b,Cx=y. Так как матрицы B и C треугольные, то данные системы легко решаются, а именно:
Эта схема вычислений называется схемой схемой Халецкого. В схеме применяется обычный контроль с помощью сумм. Схема Халецкого удобна для работы на клавишных вычислительных машинах, так, как в этом случае операции “накопления” можно проводить без записи промежуточных результатов. Рассмотрим порядок составления схемы для системы четырёх уравнений с четырьмя неизвестными. Все результаты вычислений будем записывать в одну таблицу (табл. 6). Порядок заполнения таблицы: 1) В первый раздел табл. 4 вписываем матрицу коэффициентов системы, её свободные члены и контрольные суммы. 2) Элементы столбца x1 из раздела I переносим в столбец x1 из раздела II, так как bi1=ai1 (i=1,2,3,4). 3) Вычисляем элементы первой строки раздела II. Для этого делим все элементы первой строки раздела I на элемент a11= b11. 4) Заполняем столбец x2 раздела II, начиная со второй строки. Пользуясь вышеприведенными формулами, определяем bj2. 5) Заполняем вторую строку раздела II, определяя c2j для j=3,4,5,6. 6) Заполняем столбец x3, вычисляя его элементы b33 и b43. 7) Аналогично продолжаем процесс до тех пор, пока не будет заполнен раздел II. Таким образом, заполнение раздела II происходит способом “ёлочки”: столбец – строка, столбец – строка и т.д. 8) Определяем yi и xi (i=1,2,3,4) по соответствующим формулам и записываем в разделе III. 9) Текущий контроль осуществляем с помощью столбца å, над которым производим те же действия, что и над столбцом свободных членов.
Таблица 6 Схема Халецкого
Решим, используя схему Халецкого систему уравнений
Результаты всех вычислений будем записывать в таблице (табл.7): 1) В первый раздел табл. 4 вписываем матрицу коэффициентов системы, её свободные члены и контрольные суммы. 2) Элементы столбца x1 из раздела I переносим в столбец x1 из раздела II, так как bi1=ai1 (i=1,2,3,4). 3) Вычисляем элементы первой строки раздела II. Для этого делим все элементы первой строки раздела I на элемент a11= b11, в нашем случае на 2. Имеем: c12= 4) Заполняем столбец x2 раздела II, начиная со второй строки. Пользуясь формулами, определяем bj2:
5) Заполняем вторую строку раздела II, определяя c2j для j=3,4,5,6
6) Заполняем столбец x3, вычисляя его элементы b33 и b43. Аналогично продолжаем процесс до тех пор, пока не будет заполнен раздел II. 7) Определяем yi и xi (i=1,2,3,4) и записываем их в разделе III:
Таблица 7
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 205. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

 .
. p. Затем преобразуем матрицу следующим образом: из каждой i-й неглавной строки вычитаем почленно главную строку, умноженную на mi. В результате получим матрицу, у которой все элементы q-го столбца, за исключением, аpq равны нулю. Отбрасывая этот столбец и главную строку, получим новую матрицу Mt с меньшим на единицу числом строк и столбцов.
p. Затем преобразуем матрицу следующим образом: из каждой i-й неглавной строки вычитаем почленно главную строку, умноженную на mi. В результате получим матрицу, у которой все элементы q-го столбца, за исключением, аpq равны нулю. Отбрасывая этот столбец и главную строку, получим новую матрицу Mt с меньшим на единицу числом строк и столбцов. и сравниваем с ai6.
и сравниваем с ai6. .
. =
=  =-0,292683 ; m3=
=-0,292683 ; m3=  =
=  =0,3170732; m4=
=0,3170732; m4=  =
=  =-0,256098.
=-0,256098. 1 – (-0,292683)*2=1,5853659;
1 – (-0,292683)*2=1,5853659; 2,8 – (-0,292683)*(-3,5)= 1,7756098;
2,8 – (-0,292683)*(-3,5)= 1,7756098; 3,6 – (-0,292683)*2,7=4,3902439;
3,6 – (-0,292683)*2,7=4,3902439; 2,4 – (-0,292683)*(-8,2)=0;
2,4 – (-0,292683)*(-8,2)=0; 1,2 – (-0,292683)*0,9=1,4634146;
1,2 – (-0,292683)*0,9=1,4634146; 11 – (-0,292683)*(-6,1)= 9,2146341.
11 – (-0,292683)*(-6,1)= 9,2146341. и сравниваем с
и сравниваем с  , например,
, например,  9,2146341=
9,2146341=  = -6,8963415.
= -6,8963415. = -0,257471;
= -0,257471; -0,523431.
-0,523431. . Для этого из каждой i–ой (i=2,3) строки вычитаем главную строку, умноженную на соответствующий элемент
. Для этого из каждой i–ой (i=2,3) строки вычитаем главную строку, умноженную на соответствующий элемент  . Так, при i=2 будем иметь:
. Так, при i=2 будем иметь: 1,5853659–(-0,257471)*5,5121951=
1,5853659–(-0,257471)*5,5121951= 1,7756098 – (-0,257471)*(-6,8963415)=0;
1,7756098 – (-0,257471)*(-6,8963415)=0;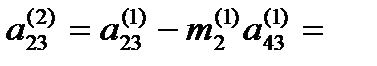 4,3902439 – (-0,257471)*5,4914634=
4,3902439 – (-0,257471)*5,4914634= 1,4634146 – (-0,257471)*10,2304878=
1,4634146 – (-0,257471)*10,2304878=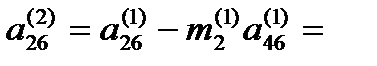 9,2146341 – (-0,257471)* 14,3378049=
9,2146341 – (-0,257471)* 14,3378049= (i=2,3) должна равняться
(i=2,3) должна равняться  ; это условие выполняется.
; это условие выполняется. =5,8041379.
=5,8041379. -0,30697. Записываем в столбец mi раздела III.
-0,30697. Записываем в столбец mi раздела III. . Для этого из третьей строки вычитаем главную строку, умноженную на соответствующий элемент
. Для этого из третьей строки вычитаем главную строку, умноженную на соответствующий элемент 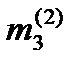 . Получаем:
. Получаем: 3,2511052 – (-0,30697)*3,2511052=
3,2511052 – (-0,30697)*3,2511052= -1,7816976 – (-0,30697)*5,8041379=0;
-1,7816976 – (-0,30697)*5,8041379=0; 19,0695844 – (-0,30697)*4,0974713=
19,0695844 – (-0,30697)*4,0974713= 20,5389920 – (-0,30697)* 2,9062069=
20,5389920 – (-0,30697)* 2,9062069= .
.

 – векторы-столбцы. Представим матрицу A в виде произведения A=BC, где B=
– векторы-столбцы. Представим матрицу A в виде произведения A=BC, где B=  , C=
, C=  .
.  и
и 
 и
и 
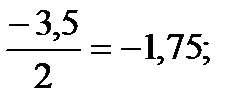 c13=
c13=  c14=
c14=  c15=
c15=  c16=
c16=