Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Кафедра математического анализаСтр 1 из 4Следующая ⇒ Метод ГАУССА и его модификации
Методические указания для лабораторных занятий и самостоятельной работы студентов по вычислительной математике специальностей Математика 050201, Информатика 050202, Физика 050203
Курган 2006 Кафедра математического анализа
Дисциплина «Математика» (специальности 050201,050202, 050203)
Составил: канд. пед. наук, доцент Михащенко Т.Н.
Составлены на основании ГОС ВПО для специальностей Математика «050201.65», Информатика «050202.65», Физика «050203.65». Методические указания могут быть использованы для проведения лабораторных занятий и организации самостоятельной работы студентов специальности 050202 – Информатика с дополнительной специальностью математика, 050201 – Математика с дополнительной специальностью информатика
Введение
Как утверждается в книге известного американского математика Валяха, 75% всех расчётных математических задач приходится на решение систем линейных алгебраических уравнений. Это не удивительно, так как математические модели тех или иных явлений или процессов либо сразу строятся как линейные, либо сводятся к таковым. Поэтому трудно переоценить роль, которую играет выбор эффективного способа решения системы линейных уравнений. Современная вычислительная математика располагает большим арсеналом методов, а математическое обеспечение ЭВМ – многими пакетами прикладных программ, позволяющих решать различные возникающие на практике линейные системы. Целью данного методического пособия является ознакомление студентов с различными модификациями самого распространенного метода решения систем линейных уравнений – метода Гаусса.  В пособии содержатся методические рекомендации по организации вычислений, задание для лабораторной работы по теме «Методы решения систем линейных уравнений», все схемы снабжены подробными инструкциями по их применению и алгоритмизированы для программирования на ЭВМ. На выбор студенту предлагается несколько модификаций проведения и оформления вычислений: полная и компактная схемы Гаусса, модификация Краута-Дулитла, схема Гаусса с выбором главного элемента и схема Халецкого.
1. Компактная схема Гаусса
Компактная схема Гаусса дает экономный способ записи вычислений и полностью соответствует традиционному методу Гаусса, изучаемому в курсе алгебры. Рассмотрим порядок составления схемы для системы четырёх уравнений с четырьмя неизвестными. Все результаты вычислений будем записывать в одну таблицу (табл. 1). Порядок заполнения таблицы, прямой ход: 1) Записываем коэффициенты данной системы в четырёх строках и пяти столбцах раздела I (табл. 1). 2) Суммируем все коэффициенты по строке и записываем сумму в столбце å (столбец контроля), например a16=
3) Делим все числа, стоящие в первой строке, на a11 и результаты b1j=a1j /a11 записываем в пятой строке раздела I. 4) Вычисляем
5) Вычисляем коэффициенты a 6) Результаты записываем в первые три строки раздела II. 7) Делаем проверку. Сумма элементов каждой строки
8) Делим все элементы первой строки раздела II на a 9) Вычисляем a 10) Делим элементы первой строки раздела III на a
11) Вычисляем a Таблица 1 Компактная схема Гаусса
Обратный ход: 12) В разделе V записываем единицы, как это указано в табл. 1, вычисляем x4=a 13) Для вычисления значений x3,x2,x1 используются лишь строки разделов I, II, III, содержащие единицы (отмеченные строки). Так для вычисления x3 умножаем x4 на b x3= b 14) Вычисляем x2, и затем x1, для чего используем элементы отмеченной строки раздела II: x2= b x1= b Компактная схема Гаусса оказывается особенно выгодной при одновременном решении нескольких систем, отличающихся лишь столбцами свободных членов, при вычислении обратной матрицы.
Решим с помощью компактной схемы Гаусса систему уравнений, все вычисления занесем в таблицу (табл.2):
Следуя порядку действий, указанному в параграфе 1, получаем значения неизвестных: x4=0,068976; х3=-1,815417; x2=0,964032; х1=4,870672.
Проверка показывает, с какой точностью получен результат, погрешность вычислений не превосходит соответственно 0,0000029; 0,0000028; 0,000001; 0,000016 в первом, втором, третьем и четвертом уравнениях.
Таблица 2
2. Модификация Краута – Дулитла
Если учесть некоторые возможности клавишных вычислительных машин, то можно составить схему вычислений, позволяющую ещё больше сократить записи промежуточных результатов по сравнению с компактной схемой Гаусса. Порядок заполнения таблицы, прямой ход: 1) Записываем коэффициенты системы aijдля i=1,2,3,4; j=1,2,3,4,5 в разделе I (табл.3). 2) Суммируем коэффициенты по каждой строке и результаты заносим в столбец å в качестве ai6 (i=1,2,3,4). 3) При i=2,3,4 находим числа mi1= ai1 / a11 и записываем их в разделе II. 4) При j=2,3,4,5,6 вычисляем коэффициенты a 5) Контроль: сумма 6) При i=3,4 находим числа тi2по формуле тi2=(ai2– mi1a12)/ a 7) При j=3,4,5,6 вычисляем коэффициенты a a 8) Находим число m43=(a43 – m41а13 – m42a 9) При j=4,5,6 находим коэффициенты a 10) Контроль: сравниваем сумму a Обратный ход осуществляется аналогично компактной схеме Гаусса. Находим неизвестные x4, x3, x2, x1 по формулам: a Таблица 3 Схема Краута – Дулитла
Количество арифметических операций в приведенной схеме и в схеме компактного метода Гаусса одинаково, поскольку операции выполняются те же самые, хотя и в другом порядке, но записи промежуточных вычислений значительно сокращаются. Последнее обстоятельство имеет большое значение при работе с клавишными вычислительными машинами.
Решим предыдущую систему с помощью схемы Краута – Дулитла систему уравнений, результаты вычислений занесем в таблицу (табл.4).
Таблица 4
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 216. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 .
. и делаем проверку. Если вычисления ведутся постоянным знаком после запятой, то числа b16 и
и делаем проверку. Если вычисления ведутся постоянным знаком после запятой, то числа b16 и  (i =2,3,4; j=2,3,4,5,6):a
(i =2,3,4; j=2,3,4,5,6):a  (i=2,3,4) не должна отличаться от a
(i=2,3,4) не должна отличаться от a  более чем на единицу последнего разряда (если все вычисления ведутся с постоянным числом знаков после запятой).
более чем на единицу последнего разряда (если все вычисления ведутся с постоянным числом знаков после запятой). и результаты записываем в четвёртой строке раздела II. Делаем проверку как в пункте 4.
и результаты записываем в четвёртой строке раздела II. Делаем проверку как в пункте 4. , a
, a b
b  , (i=3,4; j=3,4,5,6). Делаем проверку, как в пункте 6.
, (i=3,4; j=3,4,5,6). Делаем проверку, как в пункте 6. и находим числа b
и находим числа b 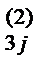 =a
=a  =a
=a  - a
- a  b
b 

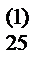


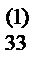







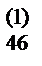
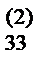










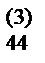


 /a
/a  .
. и получившееся произведение вычитаем из b
и получившееся произведение вычитаем из b  - b
- b  x3,
x3, 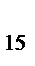 - b
- b  x4 - b
x4 - b  x3 - b
x3 - b  x2.
x2.
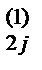 по формуле a
по формуле a  не должна отличаться от a
не должна отличаться от a  более чем на единицу последнего разряда.
более чем на единицу последнего разряда. и заносим в раздел IV.
и заносим в раздел IV. по формуле
по формуле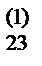 )/ a
)/ a  и записываем его в раздел VI.
и записываем его в раздел VI.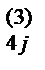 по формуле a
по формуле a 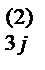 и записываем в раздел VII.
и записываем в раздел VII. + a
+ a  с числом a
с числом a  .
. x4= a
x4= a  , a
, a  x2+ a
x2+ a  x3+ a
x3+ a  x4= a
x4= a  , a11x1+a12x2+a13x3+a14x4= a15.Вычисления по этим формулам ведутся без промежуточных записей. Результаты записываются в разделе VIII таблицы.
, a11x1+a12x2+a13x3+a14x4= a15.Вычисления по этим формулам ведутся без промежуточных записей. Результаты записываются в разделе VIII таблицы.