
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Энергетический выигрыш кодированияСтр 1 из 3Следующая ⇒ Лекция №6 «Эффективность и помехоустойчивость цифровых систем передачисигналов по радиоканалам» Помехоустойчивое кодирование Практически важный вывод работ Шеннона состоит в том, что если скорость передачи информации меньше пропускной способности канала, то с использованием кодов, исправляющих ошибки, можно создать систему связи со сколь угодно малой вероятностью ошибки на выходе декодера канала. При этом адекватная система без корректирующего кодирования будет более сложной, дорогой и энергоемкой. Отсюда вывод: система, не имеющая корректирующего кодирования и работающая без ошибок, - это крайне неэффективная система. Наоборот, эффективная система должна иметь возможность работы в режиме с достаточно высокой частотой ошибок в потоке на входе декодера, а сам декодированный поток должен иметь крайне малую вероятность ошибки на бит. Энергетический выигрыш кодирования Введение при кодировании для исправления ошибок в информационный сигнал избыточных символов сопровождается негативным эффектом - снижением, при неизменной скорости цифрового потока (CDS), скорости передачи полезной нагрузки (Сinf) обратно пропорционально скорости кода (R): CDS = Clnf/R , бит/с. Отсюда следует, что для сохранения скорости передачи полезной нагрузки необходимо расширение полосы частот канала в Rраз или повышение кратности модуляции.Положительным эффектом помехоустойчивого кодирования является либо снижение вероятности ошибки, либо снижение энергетики передачи при той же вероятности ошибки, либо и то, и другое одновременно. Таким образом, кодирование расширяет возможности компромисса между полосой и энергетикой канала, присущего любой системе связи.В качестве примера системных компромиссов рассмотрим возможности выбора между кратностью относительной фазовой модуляции К = lg2M , кодовой скоростью Rи минимально необходимой полосой BN.  Положим, что кодер источника производит биты информации со скоростью Vb=1/Тb, где Тb- длительность информационного символа (тактовый интервал) в системе без кодирования. Тогда в зависимости от кратности модуляции М-позиционного сигнала ФМ требуется полоса Найквиста BN = 1/КТb. При кодировании кодом, исправляющим ошибки, скорость группового потока, состоящего из информационных и проверочных символов, возрастает в1/Rраз и становится равной у = 1/RTbсоответственно увеличивается и полоса Найквиста ВN=1/KRTb.Данные расчетов для ряда значений К и R приведены в табл.6.1 Из таблицы следует, что при передаче с неизменной скоростью Vb = const, одно и то же значение полосы Найквиста, например, BN = 1/2Тb, обеспечивается для сочетаний (К=2, R=1), (K=3, Д=2/3), (К=4, R=1/2).Какое же сочетание лучше? Ответ на этот вопрос дает параметр, называемый энергетическим выигрышем кодирования (ЭВК). Рассмотрим случай, когда передача в системах без кодирования и с кодированием производится при неизменной средней мощности Рср.В системе без кодирования вычисленная энергия одного бита информации составляет Еb = Pcp/Vb. В системе с кодированием за счет увеличения общего числа символов энергия одного бита кодированного потока снижается до значения EС = REb <Еb и Рср = EСVС. Таблица 6.1
так как в этом случае VCчисленно равна BN, или в логарифмическом виде:
Формула (6.2) показывает, что для некоторой вероятности ошибки значение отношения C/Nможет быть на 10lg(1/R) ниже, чем значение отношения Eb/N0 для той же вероятности ошибки в системе без кодирования. Эта величина является некоторой постоянной составляющей энергетического выигрыша кодирования и иногда называется выигрышем производительности.
Рис.6.1. Реально достижимый ЭВК зависит, в первую очередь, от свойств корректирующего кода и алгоритма его декодирования. В качестве примера определения ЭВК на рис. 6.1 показаны характеристики вероятности ошибки от отношения Eb/N0 для системы ФМ с кодированием и без него. Разница значенийEb/N0 между двумя кривыми по горизонтали при фиксированной вероятности ошибки (на рис.6.1 – для значений 10-3 и 10-5) и есть ЭВК (GC).Значение реального ЭВК зависит от той вероятности ошибки Ре, при которой он определяется. При возрастании C/N(снижение вероятности ошибки) ЭВК увеличивается, но до определенных пределов. Верхней границей реального ЭВК является асимптотический ЭВК, который определяется как: GA=10lg(Rdf) (6.3)
где df – свободное расстояниесверточного кода. Типичная зависимость ЭВК от вероятности ошибки канала показана на рис.6.2, где кривая соответствует использованию сверточного кода с R = 1/2, df = 5 для асимптотического ЭВК, равного 3,98 dB. |
||||||||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 1800. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
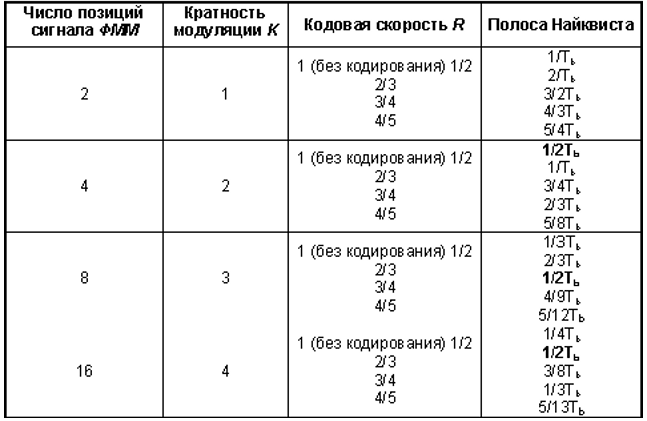


 Рис.6.2.
Рис.6.2.