
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Уравнения движения и передаточные функции объекта управления по отношению к управляющему и возмущающему воздействию.
Рисунок 3.1. Структурная схема системы по управлению.
Как было сказано выше, управляющим воздействием на объект управления является напряжение якоря «Uя». В этом случаи считаем Uя(t)=var, Ф(t)=const, Мс(t)=0. Для данного режима движение машины можно описать следующей системой уравнений:
В этой системе: Мд – момент, развиваемый двигателем; J – момент инерции двигателя и исполнительного механизма, приводимого к валу машины. Считая начальные условия нулевыми, запишем систему уравнений (3.1) в операторном виде:
Из второго уравнения системы (3.2) найдём изображение тока:
Преобразуем первое уравнение системы (3.2):
Введём некоторые обозначения:
Подставим в (3.4) выражение тока из (3.3), учтём обозначение (3.5) и вынесем за знак скобки постоянный коэффициент С·Ф, получим:
С учётом (3.6):
Определим передаточную функцию двигателя по отношению управляющему воздействию:
Подставляя свои данные, получим:
Определим каким звеном описывается данная передаточная функция:
Следовательно, двигатель постоянного тока в нашем случае является колебательным звеном. А значит, передаточная функция имеет вид:
Следовательно:
Найдём коэффициент демпфирования:
Это ещё раз подтверждает, что двигатель постоянного тока в нашем случае является колебательным звеном.  Подставим в передаточную функцию (3.13) полученные данные:
Рисунок 5.1. Структурная схема системы по возмущению.
Возмущающим воздействием на объект управления, является момент статической нагрузки Мс. В этом случаи Мс(t)=var, Ф(t)=const, Uя(t)=0. Для данного режима движение машины можно описать следующей системой уравнений:
С учетом принятых допущений, запишем систему в операторном виде:
Приравняем правые части второго и третьего уравнений системы (3.18):
Отсюда:
Подставив (3.20) в первое уравнение системы (3.18), получим:
Разделив переменные, получим:
Выполним очевидные преобразования левой и правой частей (3.22). Получим:
Введем обозначение:
Запишем передаточную функцию по отношению к возмущающему воздействию:
Применительно к исходным данным системы, передаточная функция будет иметь вид:
|
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 644. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |




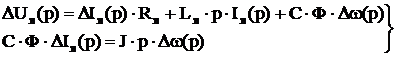

 .
.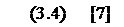
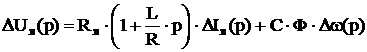 .
.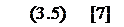
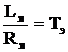 – электромагнитная постоянная времени;
– электромагнитная постоянная времени;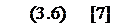
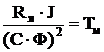 – электромеханическая постоянная времени;
– электромеханическая постоянная времени;
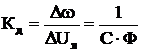 – статический коэффициент передачи.
– статический коэффициент передачи.
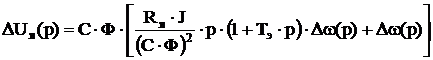 .
.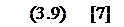
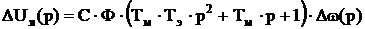
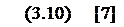
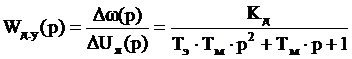 .
.
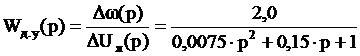 .
.
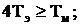
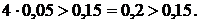

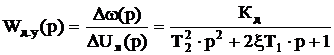 .
. Найдём постоянную времени Т и коэффициент демпфирования (коэффициент относительного затухания) ξ. Для этого приравняем знаменатели передаточных функций (3.10) и (3.13):
Найдём постоянную времени Т и коэффициент демпфирования (коэффициент относительного затухания) ξ. Для этого приравняем знаменатели передаточных функций (3.10) и (3.13): 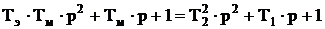 .
.

 .
.
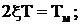

 .
.

 .
.
 .
.
 .
.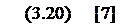
 .
.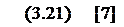

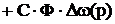 .
.
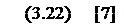
 .
.
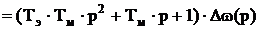
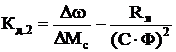 – коэффициент передачи двигателя по отношению к возмущающему воздействию.
– коэффициент передачи двигателя по отношению к возмущающему воздействию.
 .
.
 .
.