Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Основные конструкции языка (описать, пример использования)Существует три типа конструкций Verilog HDL: - поддерживаемые средствами синтеза ИС ); - неподдерживаемые средствами синтеза; - игнорируемые средствами синтеза. Сами средства синтеза могут иметь какие-либо особенности по использованию синтезируемых конструкций в конкретную технологию, некоторые конструкции могут поддерживаться одними средствами синтеза и не поддерживаться другими. Mассивы Массивы определяются для цепей и переменных, которые могут быть скалярами и векторами. Каждый элемент массива (слово) может быть как однобитным (скаляр) так и многоразрядным (вектор) reg array_a[0:7]; // массив из 8-ми однобитных переменных типа reg reg [31:0] array_b[0:15]; // массив 16-ти 32-х битных векторов типа reg // обращение к 32-битному слову с адресом 10 из массива array_b: wire[31:0] from_array_b=array_b[10]; NB: важно не путать массивыи векторы. Вектор – один элемент, который может иметь разрядность больше единицы. 4Массив - множество элементов, которые могут иметь разрядность 1 бит или n бит, м.б. многомерными *** Примеры массивов: объявление памяти: reg mem_1bit [0:1023]; // память из 1K однобитных слов reg [7:0] mem_8bit [0:1023]; // 1K восьмибитных слов - векторов типа reg Многомерные массивы: wire[3:0] farray_с [0:255] [0:127]; // двумерный массив их 4-х битовых // слов типа wire /* выборка 3-го и 2-го битов элемента с адресом [255] [127] из двумерного массива array_c */ wire [1:0] from_array_c=array_c [255] [127] [3:2]: +Смотрите в verilog.pdf Реализация комбинационной логики на Verilog В теории цифровых устройств комбинационной логикой (комбинационной схемой) называют логику функционирования устройств комбинационного типа. У комбинационных устройств состояние выхода однозначно определяется набором входных сигналов.  Пример: Автомат Мура Автомат Мура (автомат второго рода) в теории вычислений — конечный автомат, выходное значение сигнала в котором зависит лишь от текущего состояния данного автомата, и не зависит напрямую, в отличие от автомата Мили, от входных значений. Автомат Мура назван в честь его изобретателя, Эдварда Ф. Мура, опубликовавшего исследования в 1956 году в издании «Gedanken-experiments on Sequential Machines.»[1] Формальное определение Автомат Мура может быть определен как кортеж из 6 элементов, включающий: · множество внутренних состояний S (внутренний алфавит) · начальное состояние S0 · множество входных сигналов X (входной алфавит) · множество выходных сигналов Y (выходной алфавит) · функция переходов Φ(z, x) · функция выходов Ψ(z, x) Для любого автомата Мура существует эквивалентный ему автомат Мили и наоборот. Любой автомат Мура путем добавления ряда внутренних состояний может быть преобразован в автомат Мили. Способы задания · Диаграмма — изображённый на плоскости ориентированный граф, вершины которого взаимно однозначно соответствуют состояниям автомата, а дуги — входным символам. · Таблица переходов-выходов, в ячейках которой для каждой пары значений аргументов х(t), s(t) проставляются будущие внутренние состояния s(t+1). Значения выходных сигналов y(t) представляются в отдельном столбце. По способу формирования функций выходов выделяют автоматы Мили и Мура. Автомат Мили В автомате Мили (англ. Mealy machine) функция выходов Конечным детерминированным автоматом типа Мили называется совокупность пяти объектов
где S, X и Y — конечные непустые множества, а
со связью элементов множеств S, X и Y в абстрактном времени T = {0, 1, 2, …} уравнениями:
(Отображения Особенностью автомата Мили является то, что функция выходов является двухаргументной и символ в выходном канале y(t) обнаруживается только при наличии символа во входном канале x(t). Автомат Мура Зависимость выходного сигнала только от состояния представлена в автоматах типа Мура (англ. Moore machine). В автомате Мура функция выходов определяет значение выходного символа только по одному аргументу — состоянию автомата. Эту функцию называют также функцией меток, так как она каждому состоянию автомата ставит метку на выходе.
|
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 867. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 определяет значение выходного символа по классической схеме абстрактного автомата. Математическая модель автомата Мили и схема рекуррентных соотношений не отличаются от математической модели и схемы рекуррентных соотношений абстрактного автомата. Таким образом, можно дать следующее определение:
определяет значение выходного символа по классической схеме абстрактного автомата. Математическая модель автомата Мили и схема рекуррентных соотношений не отличаются от математической модели и схемы рекуррентных соотношений абстрактного автомата. Таким образом, можно дать следующее определение: ,
,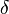 и
и  и
и