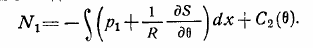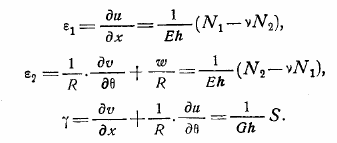Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Безмоментная теория цилиндрических оболочекСтр 1 из 2Следующая ⇒ Понятие о криволинейной системе координат Криволинейная система координат — система координат в евклидовом пространстве, или в области, содержащейся в нём. Положение произвольной точки на поверхности оболочки может быть определено пересечением двух линий на поверхности – двух криволинейных координат, за которые обычно принимают линии главных кривизн для недеформированной поверхности. Положение точки на поверхности определяется двумя характерными параметрами. В зависимости от выбора этих параметров (α и β) будем иметь ту или иную систему координат.
Примеры криволинейных координат: Полярные координаты Полярные координаты на плоскости включают расстояние r до полюса (начала координат) и направление (угол) φ. Цилиндрические координаты
Сферические координаты
Вычисление коэффициентов первой формы в цилиндрической системе координат для оболочки вращения. Рассмотрим элементарную поверхность оболочки, выделенной двумя параллельными плоскостями, отстоящими одна от другой на бесконечно малое расстояние dz и двумя меридиальными плоскостями, угол между которыми примем равным dθ.
Коэффициенты первой квадратичной формы в цилиндрической системе координат для оболочки вращения оказываются равными
Основные гипотезы теории оболочек. В основе теории упругих оболочек лежат гипотезы физический смысл которых показывается общность принципиальной постановки задачи для балок, пластинок и оболочек. 1. Прямая перпендикулярная к срединой поверхности до деформации остается прямой и перпендикулярной к деформированной срединой поверхности и не изменяет своей длины  2. Нормальные напряжения на площадках параллельных срединой поверхности пренебрежительно малы по сравнению с прочими напряжениями
Уравнения равновесия оболочек.
Геометрические уравнения оболочек.
Физические уравнения оболочек.
Граничные условия оболочек. На практике часто встречаются разнообразные граничные условия. Граничные условия могут быть кинематическими, статическими или смешанного вида. Для решения системы уравнений достаточно 4 граничных условия. Наиболее часто встречающиеся в расчетах граничные условия:
1) Шарнирно опертый неподвижный край (по линии α=const)
2) Свободноеопирание (по линии β=const)
3) Шарнирно опертый край, имеющий возможность свободно смещаться в касательной плоскости
4) Защемленный край
5) Свободный край (не возникает никаких усилий)
Основные уравнения общей теории оболочек Уравнения равновесия оболочек.
Геометрические уравнения
Физические уравнения
Основные уравнения безмоментной теории оболочек
Уравнения равновесия:
При известных усилиях N1 N2 и Sупругие перемещения определяются из системы уравнений.
Общие уравнения безмоментной теории оболочек вращения. Уравнения равновесия
Геометрические уравнения:
Безмоментная теория цилиндрических оболочек
Круговая цилиндрическая оболочка в цилиндрической системе координат
Уравнения безмоментной теории для цилиндр.оболочки R
N2 = Rp3(3) Сдвигающие усилия ( 3 подставим в 2).
Геометрические уравнения для цилиндрической оболочки
Компоненты произвольной внешней нагрузки разложены в ряд Фурье
Перемещения оболочки при нагрузке (коэффициент пуассона = 0)
|
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 399. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
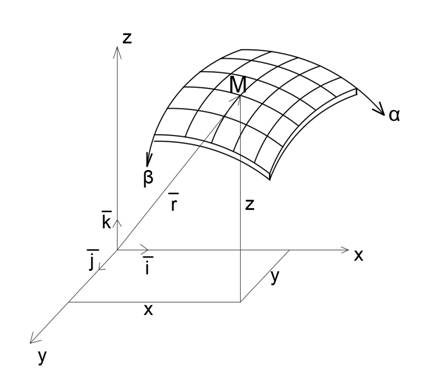

 - единичные векторы неподвижной системы координат
- единичные векторы неподвижной системы координат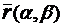 - радиус-вектор точки поверхности
- радиус-вектор точки поверхности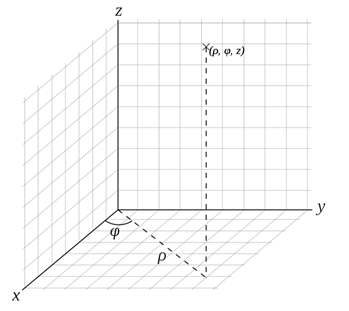







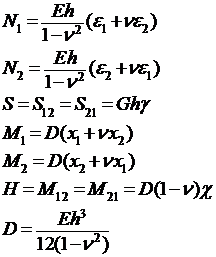










 (3 неизвN1 N2 S и 3 урав.)
(3 неизвN1 N2 S и 3 урав.)



 +
+  + Rp1 = 0 (1)
+ Rp1 = 0 (1) +R
+R  + Rp2 = 0 (2)
+ Rp2 = 0 (2)