
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Задание 2. Фильтрация сигналов для демодуляции амплитудно-манипулированных сигналов в гауссовских каналах связи.
Проделаем задание 2 аналогично заданию 1 с той лишь разницей, что в качестве модулирующего сигнала будет выступать битовая последовательность. Длительность импульса Листинг программы t=0:0.05:1; %Задаем массив отсчетов времени fc=25; %Задаем частоту несущего сигнала fm=fc/5; %Задаем частоту модулирующего сигнала Uc0=8; %Задаем амплитуду несущего колебания Um0=13; %Задаем амплитуду модулирующего сигнала Uc=Uc0*cos(2*pi*fc*t); %Задаем несущее гармоническое колебание fi0=pi/2; %Задаем начальную фазу модулирующего колебания U0=3; %Задаем постоянную составляющую модулирующего сигнала %Создадим битовую последовательность Um fori=1:1:length(t) if t(i) > 0&& t(i)<0.05 d(i) = 0; elseif t(i) > 0.05&& t(i)<0.1 d(i) = 1; elseif t(i) > 0.1&& t(i)<0.3 d(i) = 1; elseif t(i) > 0.3&& t(i)<0.75 d(i) = 0; elseif t(i) > 0.75&& t(i)<0.9 d(i) = 1; elseif t(i) > 0.9 d(i) = 0; end end Um=d; Uc=Uc0*cos(2*pi*fc*t); Um=3*Umm'; %Получение массива из матрицы-столбца Uam=Uc0.*(1+m*Um/max(abs(Um))).*cos(2*pi*fc*t); Un=Un0*randn(size(t)); Ud=Uam+Un; Udmd=filter(b,a,abs(Ud));
Построение графиков
Рис 2. Временное представление модулирующей битовой последовательности, детектируемого сигнала и демодулированного сигналов
Проделаем задание 2 аналогично заданию 1 с той лишь разницей, что в качестве модулирующего сигнала будет выступать битовая последовательность.  Длительность импульса Порядок выполнения работы: 1) Введём известные данные и посчитаем порог Байса для принятия решения
2) Из теории проверки статистических гипотез имеем: Таким образом, условная плотность распределения процесса w(y1,…,ym , t1,…,tm/s(t)≠0)= при отсутствии сигнала: w(y1,…,ym , t1,…,tm/s(t)=0)= где y1,…,ym– значение процесса
Необходимо проверить соотношение:
Так как помеха, сгенерированная в задании 2, имеет математическое ожидание МО=0 и среднеквадратическое отклонение СКО=1, то:
Листинг программы t=0:0.05:1; %Задаем массив отсчетов времени fc=25; %Задаем частоту несущего сигнала fm=fc/5; %Задаем частоту модулирующего сигнала Uc0=8; %Задаем амплитуду несущего колебания m=1; Un0=3.1; b=ones(1,3); a=1; %Создадим битовую последовательность Um fori=1:1:length(t) if t(i) > 0&& t(i)<0.05 d(i) = 0; elseif t(i) > 0.05&& t(i)<0.1 d(i) = 1; elseif t(i) > 0.1&& t(i)<0.3 d(i) = 1; elseif t(i) > 0.3&& t(i)<0.75 d(i) = 0; elseif t(i) > 0.75&& t(i)<0.9 d(i) = 1; elseif t(i) > 0.9 d(i) = 0; end end Um=d; Uc=Uc0*cos(2*pi*fc*t); Uam=Uc0.*(1+m*Um/max(abs(Um))).*cos(2*pi*fc*t); Un=Un0*rand(size(t)); Ud=Uam+Un;
Udmd=filter(b,a,abs(Ud)); U1=Un.^2; U2=Um.^2; U3=U1+U2; U4=U3'; L=sum(U4); disp('ln(Отношение правдоподобий)') disp(L)
>> Отношение правдоподобий 5.5820e+284
|
||||||||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 321. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 с;
с;


 на фоне АБГШ.
на фоне АБГШ. :
: ;
; ;
; ;
; ;
; ;
; – гипотеза о том, что в сигнале
– гипотеза о том, что в сигнале  присутствует
присутствует 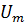 ;
; – гипотеза о том, в сигнале
– гипотеза о том, в сигнале  в дискретные моменты времени t1,…,tmимеет вид при наличии сигшнала:
в дискретные моменты времени t1,…,tmимеет вид при наличии сигшнала:

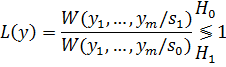


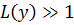 , следовательно, на основании критерия Байса принимается гипотеза
, следовательно, на основании критерия Байса принимается гипотеза 

