
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Задание 1. Демодуляция АМ-сигналаСтр 1 из 3Следующая ⇒ Пример №1 Вычислим порог для критерия Котельникова:
Для аналитического обнаружения порога рассмотрим:
Пример №2 Обнаружить цель двумя РЛС (радиолокационная станция) независимо. Априорная вероятность обнаружения цели 1-й станции равна 0,7; 2-й равна 0,8. Нужно определить вероятность обнаружения хотя бы одной станции. Решение: В таких задачах зондирующий импульс детерминированный, случайная помеха отсутствует. Нет необходимости вычислять правдоподобие. Задача сводится к вычислению элементарных событий. Соответственно, вероятность обнаружения: P(A) = 0,7 P(B) = 0,8 P(AB)= P(A)*P(B) = 0,7*0,8 = 0,56 P(C) = P(A+B)=P(A) + P(B) – P(AB)= 0,7+0,8-0,56= 0,94 или
Ответ: вероятность обнаружения одной станции P(C)=0,94. Пример №3: Генерируется два сигнала и расстояние наблюдается на интервале от 0 до t , скважность между двумя импульсами равна Решение:
Решение задачи сводится к отношению ошибочной и полезной областей, область перезагрузки приемника находится в заштрихованной области. При сближении τ1 и τ2 область перегрузки уменьшается, говоря о высокой разрешающей способности приемника. Площадь заштрихованной области равняется s, тогда искомая вероятность есть отношение:  S= T2 s= T2-(T- τ)2
τ= 0,5 c, P(A)=0,75 Оптимальное обнаружение детерминированного сигнала с учётом критических ошибок. На вход приёмника поступает либо случайный процесс в виде шума n(t), либо сумма полезного сигнала и помехи f(t). Рассмотрим две гипотезы: 1) Априорные вероятности этих гипотез принимаются равновероятными. Помеха n(t) при стрессовыхГауссовским шумом нулевым и средним и с выборочной дисперсией. В момент времени производится измерение входного процесса и по полученному значению алгоритм принимает решение: был на входе сигнал или не было. Кроме выборочного среднего и выборочной дисперсии иногда используется корреляционный момент. Из-за случайного характера процесса приёма решение в пользу гипотез Пример №4. Три источника сигнала генерируют на базовую станцию свои сигналы. Стоит задача определить вероятность потери связи Решение: Назначим априорные вероятности потерь помехоустойчивости по каждому источнику:
Возникает задача проверки гипотез, которые ведут к событию A. Гипотеза Предположим, что если помехоустойчивость снизилась у одного из источников, то вероятность потери связи равна 0,25. Если только у двоих источников, то будет равняться 0,4. Если же у всех трёх, то это число будет 0,5.
Т.е. связь не будет восстановлена. Ответ: вероятность потери связи Пример №5 Апостериорная вероятность гипотез. По каналу связи передаются сигналы в виде кодовых комбинаций S1 и S0 с априорными вероятностями их передачи P1=0.7 и Р2=0.3. Из-за наличия помех вероятность правильного каждого символа в группе уменьшается до 0.6. Искажения кодовой комбинации происходит независимо друг от друга. Фиксируем прием символов: U=10110 Определить какая команда была передана. S1=11111 P1=0.7 S0=00000 Р2=0.3 P0=0.6 U=10110 H1→S1 H0→S0 Решение: P(A(H1))=0,6*0,4*0,6*0,6*0,4=0,035 P(A(H0))=0,4*0,6*0,4*0,4*0,6=0,023 P(H1(A))= P(H0/A)=0,22 → H1
Пример 6 Имеется множество абонентов – 1000, которые разбросаны по терминалам 2G, 3G, 4G, 5G и разбросаны по трем категориям Home, Corp, VIP
Абоненты взаимодействуют с БС образуя группу событий: А1- БС обрабатывает сигнал абонента группы 2G А2- БС обрабатывает сигнал абонента группы 3G А3- БС обрабатывает сигнал абонента группы 4G А4- БС обрабатывает сигнал абонента группы 5G
1. Какова вероятность обработки базовой станцией сигнала каждого из 4-х стандартов? Возможны всего 4 исхода: Р2G=
2. Какова вероятность обработки базовой станцией сигнала любого из 4-х стандартов, но определенной группы? Возможны всего 3 исхода: PHome= 3. Какова вероятность обработки базовой станцией сигнала VIP абонента стандарта 3G? Таких всего 150 человек. Р(А) = РVIP 3G= !Примечание: если это событие Р(А) вычислять как произведение : Р(АВ) = Р3G* РVIP=0,5*0,36=0,18 ≠ 0,15 следовательно так считать нельзя. Нужно вычислять условные вероятности Р(А/В) Р(А/В) = P(3G/VIP)= P(AB)=P(B)P(A/B)=0,36*0,417=0,15 Условная вероятность выбора сигнала группы VIP из стандарта 3G P(В/А)= P(AB)=P(А)P(В/А)=0,5*0,3=0,15 4. Базовая станция равновероятно обрабатывает сигнал какого-то абонента. Какова вероятность, что этот сигнал € группе «Home»? У нас выбор сигнала по 4-м стандартам равновероятен, т.е. Р(А1)= Р(А2)= Р(А3)= Р(А4)=0,25 – априорные вероятности P(В)- полная вероятность принадлежности сигнала к группе «Home». >> >> P(B/A1)= >>Р(В)= 5. Предположим, что принятый(обработанный) сигнал € группе Home Какова вероятность того, что он был сгенерирован 3G-абонентом? >>P(A2/В)=
Задание 1. Демодуляция АМ-сигнала Порядок выполнения работы: 1) Зададим временной массив t: 0≤t≤1; 2) Зададим линейные частоты модулирующего 3) Зададим амплитуду несущего сигнала 4) Зададим коэффициент модуляции m: 0<m≤1 (при m>1 наступает перемодуляция(избыточная модуляция)), простые демодуляторы (типа квадратичного детектора) демодулируют такой сигнал с сильными искажениями. 5) Сгенерируем несущий сигнал и модулирующий сигнал, используя входные параметры:
6) Сгенерируем амплитудно-модулированный сигнал
Т.к.
7) Сгенерируем массив случайных величин (соразмерный с массивом t), распределенных по нормальный закон в интервале (0, 1) [белый шум
8) Проведем фильтрацию принимаемого сигнала Операция линейной дискретной фильтрации в общем случае описывается следующим образом:
Максимальное из чисел
Рис 1. Цифровой рекурсивный фильтр Передаточная функция фильтра имеет вид:
В среде MatLab используется функция 9) Зададим параметры фильтра:
И проведем операцию демодуляции принимаемого сигнала.
10) Вычислим отношение сигнал/шум по формуле:
Листинг программы clear t=0:0.001:1; %Задаем массив отсчетов времени fc=50; %Задаем частоту несущего сигнала fm=4; %Задаем частоту модулирующего сигнала Uc0=2; %Задаем амплитуду несущего колебания Um0=3; %Задаем амплитуду модулирующего сигнала U0=5; %Задаем постоянную составляющую модулирующего сигнала Un0=0.4; %Задаем амплитуду белого шума(Среднее квадратичное отклонение) fi0=2*pi/3; %Задаем начальную фазу модулирующего колебания m=1; %Задаем коэффициент модуляции b=ones(1,3); %Коэффиенты b цифрового фильтра a=1; %Коэффициенты a цифрового фильтра
Uc=Uc0*cos(2*pi*fc*t); %Задаем несущее гармоническое колебание Um=U0+Um0*cos(2*pi*fm*t+fi0); %Задаем модулирующий гармонический сигнал Uam=Uc0.*(1+m*Um/max(abs(Um))).*cos(2*pi*fc*t); %Выражение для АМ-сигнала Un=Un0*randn(size(t)); %Генерирует белый шум с МО=0 и СКО=1 Ud=Uam+Un; %Сигнал на входе приемника (аддитивная помеха) Udmd=filter(b,a,abs(Ud));
Построение графиков
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 353. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
||||||||||||||||||||||||||||||||||||||||||||||||||||||







 , вводится ограничение: если разница
, вводится ограничение: если разница  то приемник перегружается и выносит ошибочное решение.
то приемник перегружается и выносит ошибочное решение.  это случайные моменты поступления любых импульсов поступающих независимо от источника 1 и источника 2. Поступления от источников равновероятные. Задача определить вероятность события Р(А) что приемник будет перегружен.
это случайные моменты поступления любых импульсов поступающих независимо от источника 1 и источника 2. Поступления от источников равновероятные. Задача определить вероятность события Р(А) что приемник будет перегружен.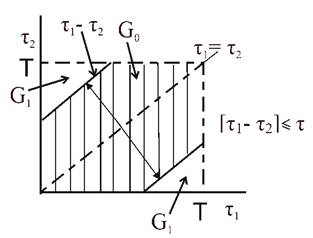 τ1 , τ2 – представляем в виде декартовых координат, а область возможных значений поступлений τ1/τ2 есть T2
τ1 , τ2 – представляем в виде декартовых координат, а область возможных значений поступлений τ1/τ2 есть T2 
 сигнал + помеха; 2)
сигнал + помеха; 2)  только помеха.
только помеха. и
и  сопровождаются ошибками двух видов: ошибка первого рода (когда отвергается правильная гипотеза) носит название ложная тревогаF; ошибка второго рода ( когда принимается не правильная гипотеза) носит название пропуск сигналаH.
сопровождаются ошибками двух видов: ошибка первого рода (когда отвергается правильная гипотеза) носит название ложная тревогаF; ошибка второго рода ( когда принимается не правильная гипотеза) носит название пропуск сигналаH. . Каждый источник из-за воздействия помех может потерять связь с базовой станцией.
. Каждый источник из-за воздействия помех может потерять связь с базовой станцией.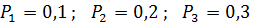
 - помехоустойчивость упала у одного источника. Гипотеза
- помехоустойчивость упала у одного источника. Гипотеза  – помехоустойчивость упала у двух источников. Гипотеза
– помехоустойчивость упала у двух источников. Гипотеза  – помехоустойчивость снизилась у всех трёх источников.
– помехоустойчивость снизилась у всех трёх источников.
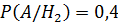



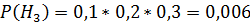

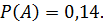
 =
= 

 - Абоненты
- Абоненты =0,1; Р3G=0,5(Р(А)); Р4G=0,15; Р5G=0,25
=0,1; Р3G=0,5(Р(А)); Р4G=0,15; Р5G=0,25
 ; Рcorp= 0,5; РVIP= 0,36(P(B))
; Рcorp= 0,5; РVIP= 0,36(P(B)) =0,15
=0,15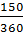 =0,417 – Условная вероятность выбора сигнала стандарта 3G из группы VIP
=0,417 – Условная вероятность выбора сигнала стандарта 3G из группы VIP =0,3
=0,3 =0,5; P(B/A2)=
=0,5; P(B/A2)=  =0,6; P(B/A3)=
=0,6; P(B/A3)=  =0,6; P(B/A4)=
=0,6; P(B/A4)=  =0;
=0;  (Аi)Р(В/ Аi)=0,5*0,25+0,6*0,25+0,6*0,25+0*0,25=0,425
(Аi)Р(В/ Аi)=0,5*0,25+0,6*0,25+0,6*0,25+0*0,25=0,425 =
=  = 0,352
= 0,352 и несущего
и несущего  колебаний.
колебаний.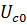 . Для модулирующего сигнала зададим амплитуду
. Для модулирующего сигнала зададим амплитуду 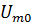 , постоянную составляющую
, постоянную составляющую  , и начальную фазу колебаний
, и начальную фазу колебаний  .
. ;
; ;
; :
: ;
; ;
; ]. Зададим его амплитуду
]. Зададим его амплитуду  . В канале связи будет создаваться аддитивная помеха, т.е. сигнал на входе приемника будет иметь вид:
. В канале связи будет создаваться аддитивная помеха, т.е. сигнал на входе приемника будет иметь вид: ;
; ;
; — отчёты входного сигнала;
— отчёты входного сигнала; — отчёты выходного сигнала;
— отчёты выходного сигнала; — постоянные коэффициенты;
— постоянные коэффициенты; и
и 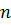 называется порядком фильтра.
называется порядком фильтра.
 ;
; .
. ;
; ;
; ;
;