
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Список индивидуальных заданий1.Пользуясь тем, что
вычислить значение sin(x) для указанного значения x0, заданного в радианах, с точностью e=0,001. Точность вычисления считается выполненной, если последнее слагаемое в (1) удовлетворяет условию |x2n-1/n!|< e. Замечание. Если Sk-значение k-го слагаемого в (1), причем S0=x, то 2. Используя представление
вычислить значение p с точностью e=0,0001. Замечание. Если n-номер слагаемого в (2), то его значение an определяется по формуле 3. Используя представление
вычислить значение ex для указанного значения x0 с точностью e=0,001. Замечание. Очередной член an=xn/n! в сумме (3) выражается через предыдущий член an-1, n=1,2, … по следующей формуле 4. Найти число M натуральных чисел ni таких, что ni2+ni3£N, где N – заданное натуральное число. 5. Найти число M натуральных чисел ni, i=1,…M и сумму 6. Найти число M натуральных чисел ni, i=1,…M таких, что и ni2<N и вычислить сумму 7. Найти число M натуральных чисел ni, i=1,…M таких, что и ni3<N и вычислить сумму 8.Пользуясь тем, что
вычислить значение cos x для указанного значения x0, заданного в радианах, с точностью e=0,001. Точность вычисления считается выполненной, если последний по модулю член в сумме (4) меньше e.  Замечание. Воспользоваться тем, что отношение последующего члена в (4) к предыдущему равно 9. Пользуясь тем, что
вычислить значение e с точностью e=0,0001. Точность вычисления считается выполненной, если последний член в сумме (5) меньше e/3. 10. Для числовой последовательности an=(n-1)/n2, n=1,2, … Найти первый член и его номер M такой, чтобы an<e, где e – заданное число, например, e=0,001 и вычислить сумму 11. Для числовой последовательности 12. Для числовой последовательности 13. Для числовой последовательности 14. Найти наименьшее натуральное число М, кратное 5, для которого 15. Найти наименьшее натуральное число М, кратное 3, для которого 16. Найти наименьшее натуральное число М, кратное 4, для которого 17. Найти наименьшее натуральное число М, кратное 6, для которого 18. Найти наименьшее натуральное число М такое, для которого 19. Найти наименьшее натуральное число М такое, для которого 20. Найти наименьшее натуральное число М такое, для которого Замечание. Воспользоваться содержанием варианта №8. 21. Найти наименьшее натуральное число М такое, для которого Замечание. Воспользоваться содержанием варианта №1. 22. Для указанного значения x0 найти наименьшее натуральное число М такое, что 23. Пользуясь тем, что
при xÎ(-1;1) вычислить значение ln(1+x) для указанного значения 24. Найти корень xс уравнения 5x3+10x2+5x-1=0 с точностью e=0,001, пользуясь формулой 25. Найти корень xс уравнения x3+12x-2=0 с точностью e=0,001, пользуясь формулой 26. Найти корень xс уравнения 2x3+4x-1=0 с точностью e=0,001, пользуясь формулой 27. Найти корень xс уравнения где n=0,1,…, m=1/3, x0=1, а=2. Точность вычисления считается достигнутой, если |xn+1-xn|<e и тогда полагают xc»xn+1. 28. Найти корень xс уравнения 29.Даны две строки s1 и s2. Пусть w – первое из слов строки s1, которое есть и в строке s2. Найти слово, предшествующее первому вхождению w в s1. 30.Даны две строки. Получить строку, в которой чередуются слова первой и второй строки. Если в одной из строк число слов больше, чем в другой, то оставшиеся слова этой строки должны быть дописаны в строку-результат.
|
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 798. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 (1)
(1) .
. (2)
(2) . Точность вычисления считается выполненной, если |an|< e.
. Точность вычисления считается выполненной, если |an|< e. (3)
(3) . Если в (3) |x|>1, то полагая x=[x]+x, где [x] – целая часть x, нужно воспользоваться формулой ex=e[x]ex. Точность вычисления считается выполненной, если |xn/n!|< e.
. Если в (3) |x|>1, то полагая x=[x]+x, где [x] – целая часть x, нужно воспользоваться формулой ex=e[x]ex. Точность вычисления считается выполненной, если |xn/n!|< e. так, чтобы выполнялось условие S£N, где N – заданное натуральное число.
так, чтобы выполнялось условие S£N, где N – заданное натуральное число.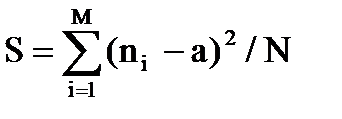 , где N, а – заданные числа, N – натуральное число.
, где N, а – заданные числа, N – натуральное число.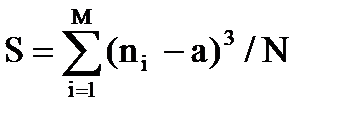 , где N, а – заданные числа, N – натуральное число.
, где N, а – заданные числа, N – натуральное число. (4)
(4)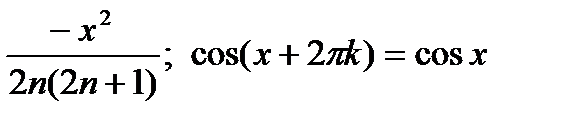 .
. (5)
(5)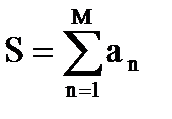 .
. , n=1,2,… найти первый член и его номер M такой, чтобы an<e, где e – заданное число, например, e=0,001 и вычислить сумму
, n=1,2,… найти первый член и его номер M такой, чтобы an<e, где e – заданное число, например, e=0,001 и вычислить сумму  , n=1,2,… найти первый член и его номер M такой, чтобы |an|<e, где e – заданное число, например, e=0,001 и вычислить сумму
, n=1,2,… найти первый член и его номер M такой, чтобы |an|<e, где e – заданное число, например, e=0,001 и вычислить сумму 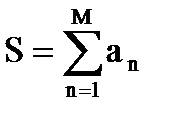 .
. , n=1,2,… найти первый член и его номер M такой, чтобы |an-4|<e, где e – заданное число, например, e=0,01 и вычислить сумму
, n=1,2,… найти первый член и его номер M такой, чтобы |an-4|<e, где e – заданное число, например, e=0,01 и вычислить сумму  .
. <e, где e=0,01, x – заданное число и вычислить сумму
<e, где e=0,01, x – заданное число и вычислить сумму  .
. <e, где e=0,01, x – заданное число и вычислить сумму
<e, где e=0,01, x – заданное число и вычислить сумму  .
.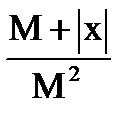 <e, где e=0,01, x – заданное число и вычислить сумму
<e, где e=0,01, x – заданное число и вычислить сумму  .
. <e, где e=0,01, x – заданное число и вычислить сумму
<e, где e=0,01, x – заданное число и вычислить сумму  .
. <e, где e=0,01 и вычислить сумму
<e, где e=0,01 и вычислить сумму  .
. <e, где e=0,01 и вычислить сумму
<e, где e=0,01 и вычислить сумму  .
. <e, где e=0,01, x=1/M и вычислить сумму
<e, где e=0,01, x=1/M и вычислить сумму  .
. <e, где e=0,01, x=1/M и вычислить сумму
<e, где e=0,01, x=1/M и вычислить сумму 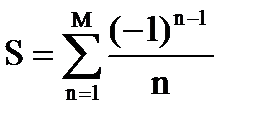 .
. £e, где e=0,01 и вычислить сумму
£e, где e=0,01 и вычислить сумму  .
. (6)
(6) , где n=0,1,…, x0=0. Точность вычисления считается достигнутой, если |xn+1-xn|<e и тогда полагают xc»xn+1.
, где n=0,1,…, x0=0. Точность вычисления считается достигнутой, если |xn+1-xn|<e и тогда полагают xc»xn+1. , где n=0,1,…, x0=0,1. Точность вычисления считается достигнутой, если |xn+1-xn|<e и тогда полагают xc»xn+1.
, где n=0,1,…, x0=0,1. Точность вычисления считается достигнутой, если |xn+1-xn|<e и тогда полагают xc»xn+1. , где n=0,1,…, x0=0,2. Точность вычисления считается достигнутой, если |xn+1-xn|<e и тогда полагают xc»xn+1.
, где n=0,1,…, x0=0,2. Точность вычисления считается достигнутой, если |xn+1-xn|<e и тогда полагают xc»xn+1. с точностью e=0,001, пользуясь формулой
с точностью e=0,001, пользуясь формулой  , (7)
, (7) с точностью e=0,00001. Замечание. Воспользоваться формулой (7), где положить m=1/5; x0=1,3; а=10.
с точностью e=0,00001. Замечание. Воспользоваться формулой (7), где положить m=1/5; x0=1,3; а=10.