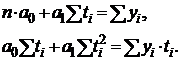Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
ИЗУЧЕНИЕ МЕТОДОВ РАСЧЕТА И ОСНОВНЫХ СВОЙСТВ СТЕПЕННЫХ СРЕДНИХ ВЕЛИЧИНЦель работы: ознакомление с порядком расчета и взаимосвязанностью степенных средних величин. Ход работы Этап 1.По значению любого количественного признака, представленного в анкете (лабораторная работа № 1), рассчитать все виды степенных средних в простой и взвешенной форме (табл. 2). Сделать вывод о соблюдении правила мажорантности степенных средних
Таблица 2 Виды степенных средних
Этап 2. Проверить выполнение важнейших свойств средней арифметической. 1. Произведение средней на сумму частот всегда равно сумме произведений вариант на частоты:
2. Если от каждой варианты отнять какое-либо произвольное число, то новая средняя уменьшится на то же число:
3. Если к каждой варианте прибавить какое-либо произвольное число, то средняя увеличится на это же число:
4. Если каждую варианту разделить на какое-либо произвольное число, то средняя уменьшится во столько же раз:
5. Если каждую варианту умножить на какое-либо число, то средняя арифметическая увеличится во столько же раз:
6. Если все частоты (веса) разделить или умножить на какое-либо число, то средняя арифметическая от этого не изменится. 7. Сумма отклонений вариант от средней арифметической всегда равна 0:
Лабораторная работа № 4 ИЗУЧЕНИЕ ВЕРОЯТНОСТНЫХ ХАРАКТЕРИСТИК СТАТИСТИКИ ПРОИЗВОДСТВЕННЫХ ФАКТОРОВ  Цель работы:ознакомление с порядком расчета показателей вариации конкретного экономического показателя. Ход работы Этап 1.Рассчитать показатели вариации по данным двух рядов динамики (табл. 3.) по заданию преподавателя. Для измерения вариации в статистике применяют несколько способов. Наиболее простым является расчет показателя размаха вариации Н как разницы между максимальным Хmax и минимальным Хmax наблюдаемыми значениями признака: H = Хmax - Хmin. Однако размах вариации показывает лишь крайние значения признака. Повторяемость промежуточных значений здесь не учитывается. Более строгими характеристиками являются показатели колеблемости относительно среднего уровня признака. Простейший показатель такого типа – среднее линейное отклонение Л как среднее арифметическое значение абсолютных отклонений признака от его среднего уровня:
При повторяемости отдельных значений Х используют формулу средней арифметической взвешенной
Напомним, что алгебраическая сумма отклонений от среднего уровня равна нулю. Таблица 3 Исходные данные для прогнозирования развития отраслей топливно-энергетического комплекса Российской Федерации
Показатель среднего линейного отклонения нашел широкое применение на практике. С его помощью анализируются, например, состав работающих, ритмичность производства, равномерность поставок материалов, разрабатываются системы материального стимулирования. Но, к сожалению, этот показатель усложняет расчеты вероятностного типа, затрудняет применение методов математической статистики. Поэтому в статистических научных исследованиях для измерения вариации чаще всего применяют показатель дисперсии. Дисперсия признака s2 определяется на основе квадратической степенной средней:
Показатель s, равный В общей теории статистики показатель дисперсии является оценкой одноименного показателя теории вероятностей и (как сумма квадратов отклонений) оценкой дисперсии в математической статистике, что позволяет использовать положения этих теоретических дисциплин для анализа социально-экономических процессов. Простыми преобразованиями могут быть получены формулы расчета дисперсии методом моментов:
Здесь X2 – среднее значение квадратов признака, или начальный момент второго порядка; Х – среднее значение признака, или начальный момент первого порядка. Коэффициент вариации до 10 % – слабая колеблемость; 10¸25 % – умеренная колеблемость; 25¸100 % – сильная колеблемость данных рассматриваемо- го ряда динамики
Этап 2.Сделать вывод о степени колеблемости экономического показателя каждого ряда динамики. Провести сравнительную характеристику полученных показателей вариации.
Лабораторная работа № 5 ИЗУЧЕНИЕ РЯДОВ ДИНАМИКИ
Цель работы:ознакомление с порядком расчета показателей, характеризующих ряды динамики. Ход работы Этап 1.Рассчитать средние уровни по данным рядов динамики (табл. 3, лабораторная работа № 4). Этап 2.По данным второго ряда динамики рассчитать все показатели анализа рядов. Порядок расчета показателей анализа ряда динамики представлен в табл. 4. Таблица 4 Показатели анализа рядов динамики
Этап 3. Провести выравнивание двух заданных рядов методом наименьших квадратов по теоретическому уравнению регрессии y = a0 + ait. Рассмотрим реализацию метода наименьших квадратов для линейной зависимости. y = a0+a1t. Данное уравнение можно классифицировать как линейную форму. Составим систему нормальных уравнений вида
Определяем неизвестные параметры a0 и a1 на основе решения этой системы уравнений методом подстановки. Расчёт промежуточных параметров, необходимых для решения системы уравнений, можно оформить в виде таблицы (табл. 5). Таблица 5 Обработка исходных данных для реализации метода наименьших квадратов
Этап 4.По полученным уравнениям трендов определить прогнозные значения показателей двух заданных рядов динамики до 2010 года. Лабораторная работа № 6 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 273. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
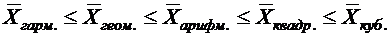
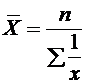
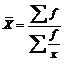
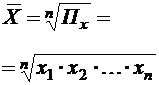
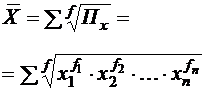
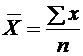
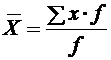
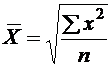
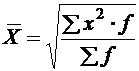
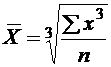
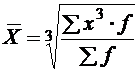
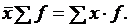
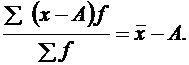
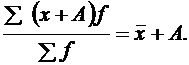
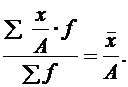
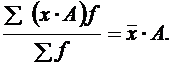
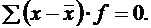
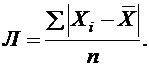
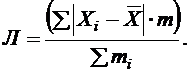
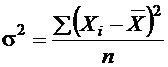 или
или 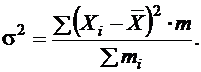
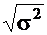 , называется средним квадратическим отклонением.
, называется средним квадратическим отклонением.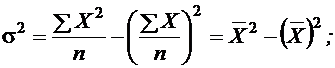

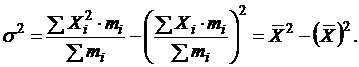
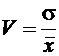 определяет степень колеблемости данных ряда динамики в соответствии с его численным значением:
определяет степень колеблемости данных ряда динамики в соответствии с его численным значением: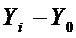
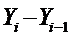 Абсолютный прирост
∆i баз; ∆i цеп
Абсолютный прирост
∆i баз; ∆i цеп
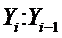 Коэффициент роста Kp
Коэффициент роста Kp
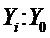
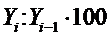
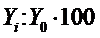
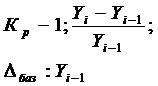 Коэффициент прироста Кпр
Коэффициент прироста Кпр
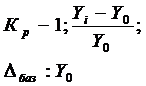
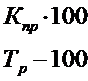 Темп прироста Тпр
Темп прироста Тпр
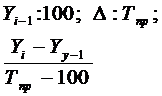
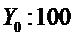 Абсолютное значение одного процента прироста А
Абсолютное значение одного процента прироста А