Лабораторная работа №2. Моделирование передающей части цифровой системы связи

Цель работы:изучение принципов формирования сигнала в системах цифровой связи.

Задачи работы:описание теоретической модели исследуемой системы передачи данных; создание модели передающего устройства цифровой сис­темы связи в Simulink; моделирование работы системы при различных на­чальных условиях; измерение основных параметров работы передающей сис­темы.

Исходные данные для работы приведены в таблице 2.1. Варианты (три вида модуляции) назначаются препода­вателем. Для студентов заочной формы обучения вариант (один) выби­рается согласно последней цифре зачетной книжки.

Таблица 2.1 Исходные данные

Для выполнения задания необходимо использовать следующие блоки:

RandomIntegerGenerator – генератор случайных целых чисел;

1-DLookupTable – таблица соответствий (истинности);

RaisedCosineTransmitFilter – формирующий фильтр с характеристикой корень из приподнятого косинуса;

Gain – усилитель сигнала;

ComplextoReal-Imag – блок выделения реальной и мнимой части ком­плексного сигнала;

Scope – осциллограф;

Discrete-TimeEyeDiagramScope – блок отображения глазковой диа­граммы сигнала;

Discrete-TimeSignalTrajectoryScope – блок отображения траектории вектора комплексной огибающей сигнала на плоскости;

Discrete-TimeScatterPlotScope – блок отображения диаграммы рассея­ния сигнала;

Subsystem – подсистема, позволяет оформить часть модели в виде от­дельного блока;

SpectrumScope – анализатор спектра сигнала.

Из указанных блоков необходимо собрать модель, показанную на ри­сунке 2.1. Modulator – подсистема формирователя сигнала цифрового пере­датчика (рис. 2.1).

Рисунок 2.1 – Общий вид модели передающей системы

В настройках генератора случайных чисел необходимо задать позици­онность созвездия (M-arynumber) согласно варианту и частоту дискретизации (SampleTime) 1/9600, что соответствует символьной скорости передачи дан­ных 9600 бод/сек. В настройках анализатора спектра (SpectrumScope) необ­ходимо выставить размер окна БПФ 1024 и включить буферизацию входного сигнала с размером буфера 1024 отсчета. Входными сигналами осциллографа являются сигнал данных и составляющие выходного комплексного сигнала передатчика, которые выделяются при помощи блока ComplextoReal-Imag.

На рисунке 2.2 показана модель формирователя сигнала. В настройках таблицы истинности (1-DLookupTable) необходимо указать соответствие между вектором входных символов и точками сигнального созвездия. В стро­ке Breakpointsукажите вектор входных символов согласно позиционности со­звездия, например, для QAM16: [ 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 ]. В стро­ке TableDataукажите точки созвездия, соответствующие входным символам, для QAM16 это: [ -3+3*i -3+1*i -3-3*i -3-1*i -1+3*i -1+1*i -1-3*i -1-1*i +3+3*i +3+1*i +3-3*i +3-1*i +1+3*i +1+1*i +1-3*i +1-1*i ]. Для манипуляций высоко­го порядка необходимо использовать методы автоматической генерации век­торов в MATLAB, например [ 0 : 1 : 255 ] и т. п.

Рисунок 2.2 – Формирователь сигнала

Ограничение спектра сигнала выполняется при помощи формирующего фильтра с характеристикой корень из приподнятого косинуса (рис. 2.3) со следующими настройками: тип фильтра (FilterType) – корень из приподнято­го косинуса (SquareRoot); групповая задержка, определяющая длину ИХ фильтра, (GroupDelay) – 5 символов; коэффициент скругления (RolloffFactor) – 0.8; коэффициент повышения частоты дискретизации (Upsamplingfactor) – 8; характер обработки сигнала (InputProcessing) – samplebased.

Комплексный сигнал с выхода формирующего фильтра поступает на усилитель, в котором выполняется его нормировка. Коэффициент передачи усилителя равен 1/K, где

где N– позиционность созвездия.

Для исследования процессов формирования сигнала необходимо ис­пользовать блоки отображения глазковых диаграмм, блоки отображения тра­ектории вектора комплексной огибающей и блоки отображения диаграммы рассеяния (рис. 2.4).

Глазковая диаграмма представляет собой “осциллограмму” аналогового демодулированного сигнала, построенную при длительности “прямого хода развертки”, равной одному символьному такту, и бесконечном “времени послесвечения экрана”. В точках оптимальной дискретизации линии на такой диаграмме образуют узкие пучки, свободное пространство между которыми по форме напоминает раскрытый глаз. В данном случае видно, что выбирать элементы из вектора y нужно начиная с первого (без дополнительного сдвига).

При прохождении сигнала через канал связи, обладающий частотной дисперсией, то есть вносящий разную групповую задержку на разных частотах, символы оказываются “размазанными” во времени и “наползают” друг на друга. Эту ситуацию и отражают диаграммы рассеяния. Минимизировать межсимвольную интерференцию удается, используя адаптивные фильтры, параметры которых автоматически подстраиваются под характеристики обрабатываемого сигнала.

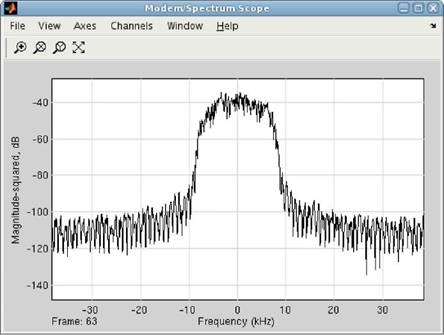
Рисунок 2.4 – Блоки отображения информации о сигналах

На рисунке 2.5 показан пример работы анализатора спектра.

При помощи трехканального осциллографа имеется возможность со­поставить сигнал данных и компоненты сигнала комплексной огибающей (рис. 2.6).

Рисунок 2.5 – Спектр формируемого сигнала

…

Рисунок 2.6 – Осциллограммы шины данных и комплексной огибающей сформированного сигнала

Порядок выполнения работы:

1) Согласно приведенным выше рисункам, создайте модель передатчи­ка в Simulink, убедитесь в ее работоспособности. Для исследования используйте сигналы с модуляциями, заданными вариантом (три сигнала).

2) Установите коэффициент скругления формирующего фильтра рав­ным 0 и запустите модель. Сохраните для отчета все графики, полученные в ходе моделирования. Произведите оценку ширины спектра сигнала, крутизны скатов, уровня первого бокового лепестка и занесите эти данные в таблицу. При помощи осциллографа оцените амплитуду квадратурных составляющих для внешних точек сигнального созвездия (точек с максимальной амплиту­дой) и для внутренних (точек с минимальной амплитудой). Занесите полу­ченные данные в таблицу, найдите отношение максимального значения к ми­нимальному.

3) Повторите задание пункта 2 для коэффициентов скругления фильтра:

- 0.2,

- 0.4,

- 0.6,

- 0.8,

- 1.

По результатам выполнения моделирования составьте отчет, который должен содержать: цели и задачи работы, вид модели в Simulink, графики, полученные при выполнении пунктов 2 и 3 (для каждого из трех сигналов), выводы по результатам модели­рования.

Вопросы для защиты лабораторного исследования

Все ответы на вопросы должны быть подтверждены либо отчетом, либо (при необходимости) демонстрацией работы исследуемой схемы.

1. Какие блоки отображения информации о сигналах предоставляет среда имитационного моделирования Simulink MATLAB. Их назначение.

2. Назначение глазковой диаграммы сигнала. Критерии распознания.

3. Назначение траектории вектора комплексной огибающей сигнала на плоскости.

4. Назначение диаграммы рассея­ния сигнала. Критерии распознания.

5. Что (какие критерии) понимается под скруглением спектра?

6. Как (по каким критериям) сигнал можно считать распознаваемым?

7. Что характеризует отношение максимального значения амплитуды сигнала (для КАМ сигналов) к ми­нимальному? Как оно сказывается на стоимости устройства?

8. Как сказывается на значении боковых лепестков, крутизны скатов и ширины спектра коэффициента скругления?

9. Каково влияние скругления на распознаваемость сигнала для каждого вида (исследованного) модуляции?

10. Какова зависимость коэффициента скругления (соответствующего распознанию сигнала) от уровня модуляции?

11. Какова зависимость отношения максимального значения амплитуды квадратурных составляющих (для внешних точек сигнального созвездия) к ми­нимальному для различного уровня модуляции?

12. …