
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Краткий теоретический материалСтр 1 из 5Следующая ⇒ МЕТОДИЧЕСКИЕ УКАЗАНИЯ к выполнению цикла лабораторных работ по дисциплине "Системы цифровой и голосовой связи" для студентов направления …
Воронеж 2016 … (рукопись) Введение Передача информационных сообщений в цифровой (дискретной) форме имеет ряд особенностей по сравнению с передачей в аналоговой (непрерывной) форме. При цифровой передаче сообщений появляется возможность уйти от аппаратурных погрешностей элементов, создавать блоки цифровой обработки сигналов с абсолютно идентичными параметрами, становится возможной регенерация (восстановление) передаваемой информации, искаженной помехами при передаче по каналу связи. Принципиально новые методы цифровой обработки сигналов позволяют создавать устройства с уникальными характеристиками, недоступными для методов аналоговой обработки сигналов. При передаче данных в дискретной форме появляется возможность обеспечить сколь угодно малую вероятность ошибки при приеме информации. Архитектура цифровой системы связи может полностью определяться на программном уровне и изменяться в процессе работы устройства для более эффективного использования спектрального и энергетического ресурса канала связи при постоянно изменяющихся условиях распространения сигнала в канале. Современные системы связи работают в условиях жесткого дефицита частотного ресурса, организация доступа к услугам сети абонентов многоканальной системы связи требует ограничения спектра сигнала от каждого абонентского передатчика для исключения взаимного влияния сигнала на сигналы других абонентов (или другой сети). В условиях постоянно возрастающих требований к цифровым системам связи по скорости передачи данных возникает необходимость в максимально возможном ограничении спектра сигнала передатчика и повышению его спектральной эффективности. Ограничение спектра сигнала происходит при помощи формирующего фильтра.  В лабораторном цикле исследуется устойчивость КАМ-сигналов различного порядка к воздействию искажения сигнала при прохождении от передатчика к приемнику. Лабораторные исследования выполняются в среде блочного имитационного моделирования Simulink MATLAB. Порядок выполнения лабораторных работ цикла
Лабораторные работы выполняются студентами индивидуально, каждому студенту отводится персональный компьютер с установленными программными средствами. В распоряжении студента так же сетевой диск, доступ к интернету. Методические указания расположены на сетевом диске в электронном виде. Работы выполняются по вариантам. Общий порядок выполнения лабораторных работ следующий: - студенты заблаговременно самостоятельно до начала лабораторного занятия знакомятся с теоретическим и методическим материалом по теме предстоящей лабораторной работы; - после краткой проверки преподавателем знаний студентов по теме лабораторной работы преподаватель объясняет цели, методы и порядок выполнения лабораторной работы; - по разрешению преподавателя студенты приступают к выполнению работы в соответствии с заданием в настоящих методических указаниях; - в ходе выполнения лабораторной работы студент может получить индивидуальные консультации, преподаватель при этом контролирует ход выполнения работы каждым студентом; - результаты расчетов, моделирования и иных позиций лабораторного исследования фиксируются в виде копии экрана компьютера (при этом для идентификации авторства на экране должна присутствовать фамилия исполнителя (например, в виде открытой папки с названием, соответствующим фамилии студента)); - по окончанию выполнения работы студент представляет преподавателю результаты (черновики) выполнения лабораторной работы; лабораторная работа считается выполненной, если получены верные результаты по каждому из лабораторных заданий; - студент, выполнив работу, должен привести лабораторное место в исходное состояние: удалить свои файлы, убрать бумаги, выключить компьютер или иное лабораторное оборудование и т.д. - к следующему занятию каждый студент представляет отчет в электронном виде и защищает результаты работы; - на этом лабораторная работа считается законченной; каждая последующая работа выполняется по этой же схеме. Допускается использовать «поисковики» сети Интернет для нахождения необходимой информации. Использовать доступ в Интернет вне тематики лабораторной работы не допускается. В отчет следует вносить адреса всех сайтов, из которых была получена информация. Результаты лабораторной работы оформляются в виде отчета (общий объем - 10-18 страниц формата А4), содержащего следующие позиции: - титульный лист (вуз, факультет, номер и название лабораторной работы, группа, Ф.И.О. студента, преподавателя, год, город); - цель лабораторной работы; - результаты выполнения работы - в соответствии с заданием, выводы; - заключение (в соответствии с целью работы). В случае пропуска занятия по уважительной причине студент может выполнить работу с другой студенческой группой. Краткий теоретический материал
Цифровая модуляция - это процесс преобразование последовательности кодовых символов в последовательность элементов сигнала. По-другому этот процесс называют манипуляцией. Существует несколько типов манипуляций: - частотная, - фазовая, - амплитудная, - квадратурная амплитудная манипуляция. При частотной манипуляции значениям «0» и «1» информационной последовательности соответствуют определенные частоты синусоидального сигнала при неизменной амплитуде. Частотная манипуляция весьма помехоустойчива, поскольку помехи телефонного канала искажают в основном амплитуду, а не частоту сигнала. Однако при частотной манипуляции неэкономно расходуется ресурс полосы частот канала. Поэтому этот вид модуляции применяется в низкоскоростных протоколах, позволяющих осуществлять связь по каналам с низким отношением сигнал/шум. Фазовая манипуляция - фаза несущего колебания меняется скачкообразно в зависимости от информационного сообщения. Амплитудная манипуляция - изменение сигнала, при котором скачкообразно меняется амплитуда несущего колебания. Квадратурная (амплитудная) модуляция (QAM) — разновидность амплитудной модуляции сигнала. Представляет собой сумму двух несущих колебаний одной частоты. Не смотря на то, что частоты равны, фазы отличаются друг от друга на 90°. Каждое колебание промодулировано по амплитуде. На выходе получаем следующую формулу. S(t) = I(t) cos(2πf0t) + Q(t)sin(2πf0t), где I (t) и Q(t) - модулирующие сигналы, f0 - несущая частота. Отличие квадратурной амплитудной манипуляцией (QASK, КАМ) от обычной квадратурной манипуляции (её называют комплексная амплитудная модуляция) заключается в том, что изменяется как фаза, так и амплитуда сигнала. Это позволяет увеличить количество информации, передаваемой одним состоянием сигнала. В англоязычной литературе такой тип манипуляции часто называют QAM, обозначение QASK применяется редко. На рис. 1 приведена упрощенная структурная схема формирователя QAM-модулированного сигнала.
Рисунок 1. Структурная схема формирователя QAM-сигнала В настоящее время наибольшее распространение получили несколько вариантов QAM. Алгоритм модуляции QAM-4 кодирует сигнал изменением фазы несущего колебания с шагом π/2. Этот алгоритм модуляции имеет название QPSK (Quadrature Phase Shift Keying - квадратурная фазовая манипуляция). Широкое распространение получили также алгоритмы QAM-16, 32, 64, 128 и 256. Алгоритм квадратурной амплитудной модуляции, по сути, является разновидностью алгоритма гармонической амплитудной модуляции и поэтому обладает следующими важными свойствами: - ширина спектра QAM модулированного колебания не превышает ширину спектра модулирующего сигнала; - положение спектра QAM модулированного колебания в частотной области определяется номиналом частоты несущего колебания. В различных типах модуляции, таких как 16 QAM, 32 QAM, 64 QAM, 128 QAM и 256 QAM. Здесь цифры относятся к числу точек на временных диаграммах, приведенных ниже. Эти диаграммы показывают число возможных состояний амплитуды и фазы сигнала. Различные особенности QAM могут быть использованы, когда данные превышают тот, который предлагается в 8-PSK, требуемый для системы радиосвязи. Это потому, что при квадратурной амплитудной модуляции достигается большое расстояние между соседними точками в плоскости IQ, распределяя очки более равномерно. И поэтому точки на диаграмме различны и ошибки данных снижаются. В то время, когда можно передавать больше бит на символ, уровни энергии остаются теми же, а точки на диаграмме должны быть ближе друг к другу, и передача становится более восприимчивы к шуму. Это приводит к более высокой вероятности ошибки, чем для более низких вариантов QAM порядка. Таким образом, существует баланс между получением высоких скоростей передачи данных и поддержания приемлемой скорости битовых ошибок для любой системы радиосвязи. Квадратурное представление сигналов является удобным и достаточно универсальным средством их описания. Квадратурное представление заключается в выражении колебания линейной комбинацией двух ортогональных составляющих – синусоидальной и косинусоидальной:
,где x(t) и y(t) – биполярные дискретные величины. Поясним работу квадратурного модулятора на примере схемы формирования сигналов четырехфазной ФМ из потока двухбитовых символов (рис. 2).
Рисунок 2 Схема квадратурного модулятора Исходная последовательность двоичных символов длительностью Т при помощи регистра сдвига разделяется на нечетные y и четные x импульсы, которые поступают на входы формирователей манипулирующих импульсов (ФМИ) соответственно квадратурного (cosωt) и синфазного (sinωt) каналов. На выходах ФМИ образуются последовательности биполярных импульсов x(t) и y(t) с амплитудой ±Um и длительностью 2Т, которые поступают на входы канальных перемножителей, где они независимо друг от друга модулируют по амплитуде два одинаковых несущих колебания, сдвинутых по фазе на 90о, т.е. находящихся в квадратуре. В результате, на их выходах формируются двухфазные (0, π) ФМ колебания. После суммирования они образуют сигнал ФМ-4 или квадратурный ФМ-сигнал. Поскольку в каждом канале осуществляется амплитудная манипуляция, этот вид модуляции называют еще квадратурной амплитудной манипуляцией или просто квадратурной амплитудной модуляцией (КАМ). Пользуясь геометрической трактовкой, каждый сигнал КАМ можно изобразить вектором в сигнальном пространстве. Причем, концы векторов в нем отображаются в виде сигнальных точек, координаты которых определяются значениями x(t) и y(t). Совокупность сигнальных точек образует, так называемое, сигнальное созвездие. В общем случае, для системы, поддерживающей m амплитудных уровней для каждого потока двоичных символов, можно образовать m2 различных комбинаций нуля и единицы. На рисунке 3 показана структурная схема модулятора и диаграмма состояний (сигнальное созвездие) системы КАМ-16, в которой x(t) и y(t) принимают значения ±1, ±3 (4-х уровневая КАМ). Как видно из рис. 3б, созвездие содержит 16 сигнальных точек, каждая из которых соответствует четырем передаваемым информационным битам.
Рисунок 3 Схема модулятора и сигнальное созвездие 16КАМ На рис. 4 показано сигнальное созвездие для системы КАМ-64, которая получается, если задается восемь амплитудных уровней для каждого потока. Из теории связи известно, что при равном числе точек в сигнальном созвездии спектр сигналов КАМ идентичен спектру сигналов ФМ. Однако помехоустойчивость систем ФМ и КАМ различна. При одинаковом числе точек сигналы системы КАМ имеют лучшую помехозащищенность, чем сигналы системы ФМ. Основная причина этого состоит в том, что расстояние между сигнальными точками в системе ФМ меньше расстояния между сигнальными точками в системе КАМ. На рис. 5 представлены сигнальные созвездия систем КАМ-16 и ФМ-16 при одинаковой нормированной мощности сигнала.
Рисунок 4 Сигнальное созвездие 64КАМ
Рисунок 5. Сигнальные созвездия 16 КАМ и 16 ФМ Расстояние d между соседними точками сигнального созвездия в системе КАМ с L уровнями модуляции определяется выражением: Аналогично при ФМ:
С увеличением порядка модуляции возрастает скорость передачи информации, то есть сигнал может нести больше бит информации на символ. Число бит, передаваемых одним состоянием, определяется N = В таблице ниже приведены резюме скоростей различных форм QAM.
Увеличение скорости передачи данных при увеличении порядка модуляции происходит в ущерб помехоустойчивости. Схемы модуляции более высокого порядка значительно меньше устойчивы к шумам и помехам. В результате этого, многие системы радиосвязи в настоящее время используют динамические методы адаптивной модуляции. Они анализируют канальные условия и могут адаптировать схему модуляции, чтобы получить самую высокую скорость передачи данных для заданных условий. Отслеживается уровень сигнал-шум, и, опираясь на него, оптимизируется система передачи. Таким путем достигается самая надежная передача данных, с наименьшим процентом ошибок. Помехоустойчивость алгоритма QAM обратно пропорциональна его спектральной эффективности. Воздействие помех приводит к возникновению неконтролируемых изменений амплитуды и фазы передаваемого по линии сигнала. При увеличении числа кодовых точек на фазовой плоскости расстояние между ними (P) уменьшается и, следовательно, возрастает вероятность ошибок при распознавании вектора Zm* на приемной стороне. Предельный уровень допустимых амплитудных и фазовых искажений QAM-модулированного сигнала представляет собой круг диаметром P.
Рисунок 6 Воздействие помех на КАМ-сигнал Центр этого круга совпадает с узлом квадратурной сетки на фазовой плоскости. Заштрихованные области на рисунке соответствуют координатам искаженного вектора QAM-модулированного колебания при воздействии на полезный сигнал помехи. |
||||||||||||||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 474. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |


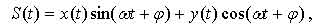



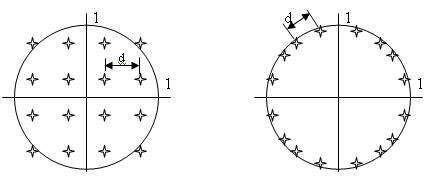

 , где М – число фаз. Так, например, при М=16 (L=4) dкам=0,471 и dфм=0,390, а при М=32 (L=6) dкам=0,283, dфм=0,196.
, где М – число фаз. Так, например, при М=16 (L=4) dкам=0,471 и dфм=0,390, а при М=32 (L=6) dкам=0,283, dфм=0,196. , где T – уровень модуляции.
, где T – уровень модуляции.