Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Середні характеристики рядів динамікиДля узагальнюючої характеристики динаміки досліджуваного явища за ряд періодів визначають різного роду середні показники. Є дві категорії таких показників: 1) середні рівні ряду; 2) середні показники змін рівнів ряду. Метод обчислення середнього рівня динамічного ряду залежить від виду ряду динаміки. В інтервальному ряді абсолютних величин з рівними періодами часу використовується середня арифметична проста: де n – число рівнів ряду, уі – рівні ряду. У моментному ряді, при умові рівномірної зміни показника між датами, середня розраховується за формулою середньої хронологічної:
У моментних та інтервальних рядах динаміки з нерівними періодами (проміжками) часу для обчислення середнього рівня ряду використовують середню арифметичну зважену: де У – рівні ряду, t – проміжки часу між суміжними датами або періоди часу. Узагальнюючими характеристиками інтенсивності динаміки є середній абсолютний приріст та середній темп зростання. Середній абсолютний приріст (абсолютна швидкість динаміки) показує на скільки одиниць у середньому за одиницю часу за певний період змінювався рівень показника, що аналізується. Розраховується середній абсолютний приріст діленням загального приросту за весь період на довжину цього періоду.  де За базисними абсолютними приростами середній показник розраховується таким чином: Середній темп зростання показує у скільки разів у середньому за одиницю часу за певний період змінювався рівень показника, що аналізується і обчислюється за формулою середньої геометричної із ланцюгових темпів зростання:
де n – кількість темпів зростання за однакові інтервали часу. Врахувавши взаємозв’язок ланцюгових і базисних темпів зростання, формулу середньої геометричної можна записати так:
Отже, середній темп зростання можна розрахувати на основі: а) ланцюгових темпів зростання; б) кінцевого базисного (за весь період) темпу зростання; в) кінцевого Уn і базисного Уо рівнів ряду. Середній темп приросту – це показник, який показує на скільки відсотків у середньому за одиницю часу за певний період змінювався рівень показника, що аналізується і розраховується за формулою:
Результати розрахунків базисних та ланцюгових показників ряду динаміки і значення показників представляють у таблиці наступної форми (табл. 3.1). Рівень ряду динаміки обирається відповідно до теми курсової роботи, вихідна інформація виписується із додатку до методички за 9 років.
Таблиця 3.1 Показники динаміки (назва показника)
Аналіз тенденції розвитку (розділ 3.2) являється одним із завдань статистики в процесі аналізу рядів динаміки і полягає у виявленні закономірностей зміни рівнів ряду, тобто визначення загальної тенденції розвитку. Для встановлення загальних закономірностей розвитку суспільних явищ за даними динамічних рядів їх обробляють за допомогою методів, які можна розділити на механічні та аналітичні. Механічне вирівнювання рядів динаміки здійснюють шляхом застосуванням таких прийомів: укрупнення періодів і обчислення за ними середніх показників із наступним їх аналізом; переведення абсолютних показників динамічних рядів у відносні, за рахунок чого досягається порівнянність багатомірних динамічних рядів. Для вивчення тенденції застосовують метод вирівнювання ряду динаміки за середнім абсолютним приростом, що передбачає заміну фактичних рівнів ряду динаміки вирівняними за наступною формулою: y = yt + At, де у – вирівняні значення рівня ряду динаміки, t – порядковий номер року, А – середній абсолютний приріст рівня ряду динаміки. Метод збільшення інтервалів – це один із найпростіших способів виявлення загальної тенденції розвитку явища, суть якого полягає в тому, що первинний ряд динаміки перетворюється і замінюється іншим, показники якого відносяться до більш триваліших періодів часу. Новостворений ряд може складатися із абсолютних величин за укрупнені періоди часу (ці величини одержують шляхом додавання рівнів первинного ряду абсолютних величин), або із середніх величин по інтервалах. При додаванні рівнів або при виведенні середніх по укрупнених інтервалах взаємозрівноважуються коливання первинного ряду, внаслідок чого тенденція розвитку вирізняється чіткіше. Залежно від схеми формування інтервалів розрізняють ступінчасті та плинні середні. Плинна середня більш гнучка і може краще відобразити особливості тенденції розвитку явища. Аналітичне вирівнювання ряду динаміки – це найбільш досконалий прийом виявлення основної тенденції динаміки. При аналітичному вирівнюванні динамічного ряду фактичні значення У, замінюються обчисленими на основі певної функції У = f(t), яку називають трендовим рівнянням (t – змінна часу). Вибір типу функції ґрунтується на попередньому теоретичному аналізі суті явища, яке вивчається, і характеру його динаміки. Якщо ланцюгові абсолютні прирости відносно стабільні, вирівнювання ряду виконується на основі лінійної функції: Уt = а + bt. У зазначених функціях t – порядковий номер періоду (дати), а – рівень ряду при t = 0. Параметр b характеризує швидкість динаміки: середню абсолютну в лінійній функції і середню відносну – в експоненті. Коли характеристики швидкості розвитку зростають (або зменшуються), використовують інші функції (парабола 2-го степеня, модифікована експонента тощо). Параметри трендових рівнянь визначають методом найменших квадратів. Згідно з умовою мінімізації суми квадратів відхилень фактичних рівнів ряду уt від теоретичних Уt, параметри визначаються розв’язуванням системи нормальних рівнянь. Для лінійної функції вона записується так:
Система рівнянь спрощується, якщо початок відліку часу (t = 0) перенести в середину динамічного ряду. Тоді значення t, які розміщені вище середини, будуть від’ємними, а нижче – додатними. При непарному числі членів ряду (наприклад, n = 5) змінній t надаються значення з інтервалом одиниця: -2, -1, 0, 1, 2; при парному (наприклад, n = 6) – з інтервалом два: -5, -3, -1, 1, 3, 5. В обох випадках система рівнянь суттєво спрощується і формули розрахунку параметрів трендового рівняння набувають вигляду:
Щоб оцінити ступінь наближення одержаного лінійного тренду до фактичних даних, визначимо показники їх коливання відносно тренду. Залишкове середнє квадратичне відхилення становитиме: де m – число параметрів рівняння тренду, m = 2 – для лінійного тренду (m = 3 – для параболічного тренду). Коефіцієнт варіації (квадратичний):
(6.13)
Результати вирівнювання навести в таблицях 3.2, 3.3, 3.4.
Таблиця 3.2 Вирівнювання ряду динаміки за середнім абсолютним приростом
Таблиця 3.3 Згладжування ряду динаміки за способом визначення середньої для укрупнених періодів і ковзних укрупнених періодів
Таблиця 3.4 Розрахунок параметрів для аналітичного вирівнювання
Також необхідно здійснити аналітичне вирівнювання за допомогою ПК комп’ютерної програми Exсel.
Таблиця 3.5 Вихідні дані для здійснення аналітичного вирівнювання за допомогою програми Excel
Розрахувати за допомогою комп’ютера лінійну та параболічну тенденцію досліджуваного в динаміці показника відповідно до теми.
Таблиця 3.6 Розрахунок перспективної урожайності _____ в ___ за лінійною та параболічною тенденцією
Визначення показників варіації при аналізі середньої урожайності сільськогосподарських культур (продуктивності сільськогосподарських тварин) (розділ 3.3 для тем №1-8). Середні величини дають узагальнюючу характеристику сукупностей за певною варіюючою ознакою. Вивчення розміру відхилень та їх розподілу використовують для оцінки кількісної однорідності сукупності. Вимірювання і аналіз варіації має велике значення для оцінки стійкості досліджуваних явищ, а також впливу різних факторів на коливання ознак. Для розрахунку цих показників необхідно використовувати макет таблиці 3.7.
Таблиця 3.7 Вихідна інформація для обчислення середньої урожайності зернових за 2004-2012 роки
1.Середнє значення варіюючої ознаки (відповідно до теми) обчислюється за формулою середньої арифметичної зваженої: 2. Показники варіації а) розмах варіації: б) дисперсія:
в) середнє квадратичне відхилення:
г) коефіцієнт варіації:
Одним з основних методів статистичного дослідження є зведення і групування статистичних даних. При застосуванні цього методу в курсовій роботі слід віддати перевагу аналітичному групуванню для встановлення зв’язку між явищами (розділ 3.4). По-перше, важливе значення має вибір групувальної (факторної) та результативної ознак. За факторною (групувальною) ознакою здійснюється розподіл сукупності на однорідні групи за суттєвими для них ознаками. По-друге, побудувати ранжируваний ряд господарств за групувальною ознакою (в порядку її зростання). По-третє, визначити інтервал групування. При малій вибірці, коли кількість одиниць сукупності не перевищує 25-30, їх розподіляють на 3 групи. Величину інтервалу при групуванні визначають за формулою: де і – величина інтервалу; На основі проведених групувань потрібно зробити висновки, зазначити закономірності розподілу, взаємозв’язку і взаємозалежності. їх потрібно підтвердити цифрами, особливу увагу звернути на виявлене відхилення від встановлених закономірностей і розкрити можливі причини цього. Вихідна інформація для проведення статистичного групування обирається відповідно до теми в обсязі 20 рядків по кожному необхідному показнику (номер рядку, за яким проводиться дослідження та 19 наступних номерів). Для тем №1-5 обсяг вихідної інформації має бути представлений показниками в розрізі культур: посівна площа, валовий збір, загальний обсяг внесених добрив на всю площу. В якості факторної ознаки обирається рівень внесення добрив на 1 га, в якості результативної ознаки – урожайність по певній сільськогосподарській культурі. Для тем № 6-8 обсяг вихідної інформації має бути представлений такими показниками як: середньорічне поголів’я тварин, валовий вихід продукції тваринництва, рівень витрачання кормів. В якості факторної ознаки обирається рівень годівлі 1 гол, а в якості результативної ознаки – продуктивність тварин (середньорічний вихід продукції від 1 голови). Для тем №9-13 обсяг вихідної інформації має бути представлений показниками в розрізі культур: посівна площа, валовий збір, загальний розмір виробничих витрат. В якості факторної ознаки обирається урожайність, в якості результативної ознаки – собівартість 1 ц продукції. Для тем №14-16 обсяг вихідної інформації має бути представлений показниками в розрізі культур: середньорічне поголів’я тварин, валовий вихід продукції, загальна сума виробничих витрат. В якості факторної ознаки обирається продуктивність тварин, в якості результативної ознаки – собівартість 1 ц продукції. Приклад наведено у таблиці 3.8.
Таблиця 3.8 Групування ранжируваного ряду господарств району за середньорічним надоєм молока на 1 корову
Для тем №17-21 обсяг вихідної інформації має бути представлений показниками в розрізі культур: посівна площа, валовий збір, прямі затрати праці на всю продукцію. В якості факторної ознаки обирається урожайність, в якості результативної ознаки – затрати праці на 1 ц продукції. Для тем №22-23 обсяг вихідної інформації має бути представлений показниками в розрізі видів продукції тваринництва: середньорічне поголів’я тварин, валовий вихід продукції, прямі затрати праці на всю продукцію. В якості факторної ознаки обирається продуктивність тварин, в якості результативної ознаки – затрати праці на 1 ц продукції (трудомісткість). Для тем №24-30 обсяг вихідної інформації має бути представлений показниками в розрізі видів продукції: валовий збір (валовий вихід продукції), загальний розмір виробничих витрат, виручка від реалізації (чистий дохід від реалізації). В якості факторної ознаки обирається собівартість 1 ц продукції, в якості результативної ознаки – прибуток від реалізації 1 ц продукції (ціна – собівартість). Макети таблиць для здійснення групування за темами №9-13.
Таблиця 3.9 Ранжируваний ряд за урожайністю
Таблиця 3.10 Вплив урожайності на собівартість 1 ц
Одним із завдань, які вирішуються в ходу дослідження, є вивчення взаємозв’язку між явищами, для чого використовують кореляційний метод аналізу (розділ 3.5). При кореляційному зв’язку, який має ймовірний характер, немає суворої відповідності між значеннями залежних ознак: кожному певному значенню аргументу (факторної ознаки) відповідає кілька різних значень функції (результативної ознаки). Рівняння, за допомогою яких визначають статистичний зв’язок між корелюючими величинами, називають рівнянням регресії, а лінії, побудовані на їх основі – лініями регресії. Зв’язок між результативною та факторною ознаками може бути прямолінійним та криволінійним. У випадку прямолінійної форми зв’язку результативна ознака змінюється під впливом факторної рівномірно, тому що форму зв’язку можна виразити у вигляді наступного рівняння прямої лінії: yx = a0+ а1х, (6.20) де yx – теоретичні (розраховані за рівнянням регресії) значення результативної ознаки; a0 – початок відліку, або значення при умові, що х=0; а1 – коефіцієнт регресії (коефіцієнт пропорційності), який показує, як змінюється yx при кожній зміні х на одиницю; х – значення факторної ознаки. Для оцінки щільності та напрямку зв’язку між факторною та результативною ознаками (які вже обиралися у п. 3.4) використовуємо функцію «Регресія» програми Excel. Після отримання підсумків необхідно їх оцінити, зробити висновки та побудувати графік кореляційної залежності. За допомогою індексного методу вирішують такі завдання: - одержують порівняльну характеристику зміни явища у часі, де вони виступають як показники динаміки; - оцінюють роль окремих факторів, що формують складне явище; - дають порівняльну характеристику зміни явищ у просторі. У цьому разі індекси забезпечують територіальні порівняння. Статистичний індекс – це відносний показник, що характеризує зміну рівня будь-якого суспільного явища в часі, просторі чи порівняно з планом, нормою, стандартом. Так як і відносні величини, одержані в результаті порівняння однойменних величин, індекси можуть бути виражені у формі коефіцієнта або відсотків. Вихідна інформація для проведення індексного аналізу береться по декільком видам продукції рослинництва (тваринництва) за останні два роки. Таблиця 3.11 Виробництво і собівартість продукції технічних культур в господарстві характеризують дані таблиці:
Визначте: - агрегатний індекс собівартості, індекс фізичного обсягу продукції та загальний індекс виробничих витрат; - абсолютну економію (перевитрати) коштів в звітному році в порівнянні з базисним, в тому числі за рахунок зміни собівартості і фізичного обсягу продукції. Зробити короткі висновки. Формули індексів, які треба визначити: Агрегатні (постійного складу) індекси: - собівартості:
- фізичного обсягу продукції:
Загальний індекс виробничих витрат, враховуючи економічну формулу В=z х q,має вигляд:
Таблиця 3.12 Вихідні дані для аналізу продуктивності праці
Вартісний індекс продуктивності праці (змінного складу) :
Таблиця 3.11 Вихідні дані про обсяг виробленої продукції та затрати робочого часу
Загальний трудовий індекс постійного складу
Абсолютна економія(перевитрати) затрат робочого часу за рахунок зміни рівня продуктивності праці за всіма видами продукції ∆Т∑=Т01-Т1 Вона визначається також як алгебраїчна сума економії(+) або перевитрат(-) затрат робочого часу за кожним видом продукції: ∆Т∑=∆То +∆Тцб +∆Тм Відносний рівень економії затрат робочого часу визначається за допомогою індексу економії затрат робочого часу :
РЕКОМЕНДОВАНА ЛІТЕРАТУРА
ДОДАТКИ
Додаток А
Таблиця для визначення номеру рядка вихідної інформації
Додаток Б
Бланк-завдання |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 384. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 , (6.2)
, (6.2) . (6.3)
. (6.3) , (6.4)
, (6.4) , (6.5)
, (6.5) – ланцюгові абсолютні прирости, n – число рівнів ряду.
– ланцюгові абсолютні прирости, n – число рівнів ряду.
 . (6.6)
. (6.6) , (6.7)
, (6.7) . (6.8)
. (6.8) . (6.9)
. (6.9) . (6.10)
. (6.10) . (6.11)
. (6.11) , (6.12)
, (6.12)
 t = а0 + а1 t
t = а0 + а1 t



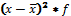
 =
=  . (6.14)
. (6.14) =
=  -
-  . (6.15)
. (6.15) . (6.16)
. (6.16) . (6.17)
. (6.17)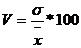 (6.18)
(6.18) , (6.19)
, (6.19) – максимальна величина групувальної ознаки;
– максимальна величина групувальної ознаки; 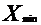 – мінімальна величина групувальної ознаки; n – кількість груп.
– мінімальна величина групувальної ознаки; n – кількість груп. , (6.21)
, (6.21) . (6.22)
. (6.22) . (6.23)
. (6.23)