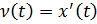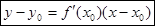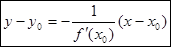Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Задачи, приводящие к понятию производной, ее определение, геометрический и механический смысл. Уравнение касательной и нормали. ⇐ ПредыдущаяСтр 2 из 2 Производной функции y = f(x) в точке x0 называется предел отношения приращения функции к приращению аргумента, когда приращение аргумента стремится к нулю. 1) Пусть материальная точка движется неравномерно по некоторой прямой. Расстояние S зависит от истекшего времени t, то есть S = S(t). Пусть за промежуток времени
2) Предел средней скорости движения при стремлении к нулю промежутка времени
Геометрический смысл производной состоит в том, что производная функции Механический смысл производной: скорость – это производная координаты по времени: Уравнение касательной - Уравнение нормали - |
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 244. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
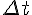 перемещение точки будет составлять
перемещение точки будет составлять 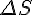 . Тогда средняя скорость движения точки за этот промежуток времени равна:
. Тогда средняя скорость движения точки за этот промежуток времени равна: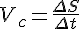
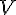 , получим:
, получим: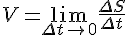 .
.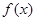 при данном значении
при данном значении 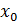 равна угловому коэффициенту касательной к графику этой функции в т. М0(
равна угловому коэффициенту касательной к графику этой функции в т. М0( 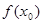 ).
).