
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Непрерывность функции, точки разрыва. Свойства непрерывных функций.Стр 1 из 2Следующая ⇒ Предел функции в точке. Односторонние пределы. Односторонний пределчисловой функции – «приближение» к предельной точке с одной стороны. Такие пределы называют соответственно левым и правым пределом. Правый предел обозначается Левый предел обозначается Определение предела функции по Коши:Число Определение предела функции по Гейне:Число
Бесконечно малые и бесконечно большие функции и их связь. Сравнение бесконечно малых, связь предела функции с бесконечной малой. Функция y=f(x) называется бесконечно малой при x→a или при x→∞, если Функция называется бесконечно большойпри Если
Если Если Бесконечно малая функция a называется бесконечно малой порядка kотносительно бесконечно малой функции b, если предел
Основные теоремы о пределах. Замечательные пределы. Приемы вычисления пределов. 1. Замечательные пределы: 
Техника вычисления пределов а) Чтобы раскрыть неопределенность типа
Непрерывность функции, точки разрыва. Свойства непрерывных функций. Функция 1) определена в точке 2) имеет конечные односторонние пределы функции при 3) эти пределы равны значению функции в точке Точки разрыва – точки, в которых нарушается непрерывность функции. Точка Если Если Точка Свойства непрерывных функций: 1) Если функция f(x) непрерывна в промежутке (a,b), то существует в этом промежутке, по крайней мере, одно такое значение х, при котором f(х) принимает свое набольшее значение и, по крайней мере, одно такое значение х, пр котором функция принимает свое наименьшее значение. 2) Если функция f(x) непрерывна в промежутке (a,b), причем f(a)=m и f(b)=n, и если k – любое число, заключающееся между m и n, то существует в промежутке (a,b), по крайней мере, одно такое значение х, при котором значение f(x) равно k; в частности, если f(a) и f(b) разных знаков, то существует внутри промежутка (a,b), по крайней мере, одно такое значение х, при котором f(x) обращается в ноль. |
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 274. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
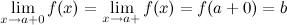
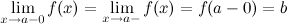
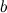 называется пределом функции
называется пределом функции 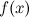 в точке
в точке  , если для
, если для 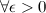
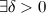 такое, что для
такое, что для 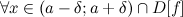 из того, что
из того, что 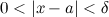 следует, что
следует, что 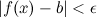 :
: 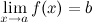 или
или 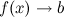 при
при 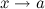 .
.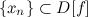 , которая сходится к
, которая сходится к 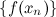 сходится к
сходится к 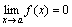 или
или 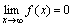 , т.е. бесконечно малая функция – это функция, предел которой в данной точке равен нулю.
, т.е. бесконечно малая функция – это функция, предел которой в данной точке равен нулю.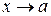 , где
, где 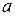 – число или одна из величин
– число или одна из величин 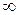 ,
, 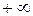 или
или 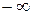 , если
, если 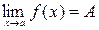 , где
, где 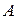 – число или одна из величин
– число или одна из величин 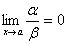 , то функция a называется бесконечно малой более высокого порядка, чем функция b.
, то функция a называется бесконечно малой более высокого порядка, чем функция b.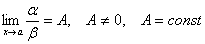 , то a и b называются бесконечно малыми одного порядка.
, то a и b называются бесконечно малыми одного порядка.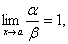 то функции a и b называются эквивалентными бесконечно малыми. Записывают a ~ b.
то функции a и b называются эквивалентными бесконечно малыми. Записывают a ~ b.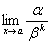 конечен и отличен от нуля.
конечен и отличен от нуля.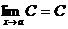
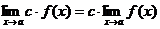
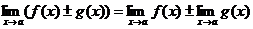
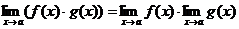
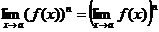
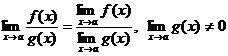
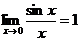
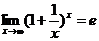
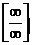 , необходимо числитель и знаменатель дроби разделить на наибольшую степень переменной.
, необходимо числитель и знаменатель дроби разделить на наибольшую степень переменной. 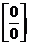 , где под знаком предела стоит рациональная дробь, достаточно числить и знаменатель дроби разложить на множители и затем сократить дробь на множитель, приводящий к неопределенности.
, где под знаком предела стоит рациональная дробь, достаточно числить и знаменатель дроби разложить на множители и затем сократить дробь на множитель, приводящий к неопределенности. 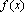 называетсянепрерывной в точке
называетсянепрерывной в точке  , если она удовлетворяет следующим условиям:
, если она удовлетворяет следующим условиям: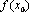 ;
;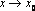 слева и справа;
слева и справа;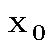 называетсяточкой разрыва первого рода функции
называетсяточкой разрыва первого рода функции 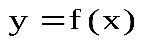 , если в этой точке существуют конечные односторонние пределы, т.е.
, если в этой точке существуют конечные односторонние пределы, т.е. 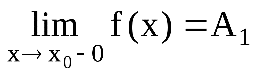 и
и 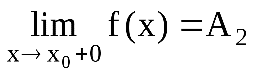 . При этом:
. При этом: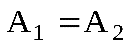 , то точка
, то точка 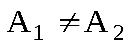 , то точка
, то точка