
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Среднеквадратическое приближение таблично заданных функций ⇐ ПредыдущаяСтр 2 из 2 (метод наименьших квадратов) Пусть в узлах x0, x1, … , xn имеем значения у0, у1, … , уn функции f(x). Среди полиномов m-й степени (m<n) Pm(x) = a0 + a1x + a2x2 + … + amxm(1) найти такой, который доставляет минимум выражению S= Неизвестными являются коэффициенты полинома (1). Сумма (2) представляет собой квадратичную форму от этих коэффициентов. Кроме того, формула (2) показывает, что функция S = S(a0, a1, … , am) не может принимать отрицательных значений. Следовательно, минимум функции S существует. Применяя необходимые условия экстремума функции S = S(a0, a1, … , am), получаем систему линейных алгебраических уравнений для определения коэффициентов a0, a1, … , am:
Полагая сp = Сa = d, (4) где С = Если среди узлов x0, x1, … , xn нет совпадающих и m ≤ n, то система (4) имеет единственное решение a0 =
является единственным полиномом степени m, обладающим минимальным квадратичным отклонением S* = Smin. Погрешность среднеквадратического приближения функции характеризуется величиной δ = Самый простой и наиболее часто используемый вид аппроксимации (среднеквадратического приближения) функции – линейная. Приближение данных (xi, yi) осуществляется линейной функцией y(х)= ax + b. На координатной плоскости (x, y) линейная функция, как известно, представляется прямой линией. Пример. Сгладить систему точек прямойy= ax + b. 
Строим рабочую таблицу:
Система для определенияa и b имеет вид: формул Крамера: Δ = a = Искомое уравнение y= 0,74x + 1,55.
Программылинейной и квадратичной аппроксимации на PASCAL’е и MATHCAD’е Линейная аппроксимация Программа в PASCAL’е для линейной аппроксимации Дана зависимость теплоемкости (Сp) от температуры (Т). Найти коэффициенты линейной аппроксимирующей функции a и b. Записать вид полученной линейной аппроксимирующей функции. Найти теплоемкость (Сp) при температуре Т = 550 К.
Обозначения в программе: n – количество известных экспериментальных значений; x – экспериментальные значения x (температура); y – экспериментальные значения y (теплоемкость);S1, S2, S3, S4 – суммы; a0, a1 – коэффициенты аппроксимирующей функции; x0 – температура, при которой надо найти теплоемкость; y0 – теплоемкость при заданной температуре. ProgramLinApr; constn=8; x: array[1..n] ofreal=(300,400,500,600,700,800,900,1000); y: array[1..n] ofreal=(6.97,7.01,7.12,7.28,7.45,7.62,7.79,7.93); varS1, S2, S3, S4, a0, a1, x0, y0: real; i: integer; Begin // Расчетсумм: S1:=0; S2:=0; S3:=0; S4:=0; fori:=1 tondo beginS1:=S1+x[i]; S2:=S2+y[i]; S3:=S3+sqr(x[i]); S4:=S4+x[i]*y[i]; end; // Расчет коэффициентов аппроксимирующей функции: a0:=(S2*S3-S4*S1)/(n*S3-sqr(S1)); a1:=(n*S4-S1*S2)/(n*S3-S1*S1); // Вывод на экран коэффициентов аппроксимирующей функции: writeln('Коэффициенты аппроксимирующей функции:'); writeln('a0=', a0:1:3); writeln('a1=', a1:1:5); // Вывод на экран аппроксимирующей функции: writeln('Аппроксимирующая функция:Cp=', a0:1:3, '+',a1:1:5,'*T'); // Задаем температуру, при которой нужно посчитать теплоемкость: x0:=550; // Расчет теплоемкости при заданной температуре: y0:=a0+a1*x0; // Вывод на экран теплоемкости при заданной температуре: writeln('При Т=', x0, ' К', ' Cp=', y0:1:2, ' Дж/моль*К'); end. Окно вывода Коэффициенты аппроксимирующей функции: a0=6.445 a1=0.00146 Аппроксимирующаяфункция:Cp=6.445+0.00146*T При Т=550 К Cp=7.25 Дж/моль*К
В MATHCAD’е линейная аппроксимация реализуется с помощью двух программ. Приведем первую из них, которых работает с действительными числами:
Здесь:line(x,y) – вектор из двух элементов (b,a)коэффициентов линейного полинома ax + b: b = line(x,y)0, a = line(x,y)1.
Программа в PASCAL’е для квадратичной аппроксимации Длятаблично заданной функции построить аппроксимирующий полином 2-й степени:
Здесь:<Ф> – количество букв в фамилии студента; <И> – количество букв в имени студента; <О> – количество букв в отчестве студента;
ProgramIVANOV_naim_kvadr_polinom_2; Var w,w0,w1,w2,a0,a1,a2,er,z:real; i,p:integer; x,y:array[1..5] ofreal; c:array[0..4] ofreal; d:array[0..4] ofreal; functionstepen(u:real;k:integer):real; varg:real; m:integer; Begin g:=1; form:=1 tok dog:=g*u; stepen:=g; end; Begin writeln(' СЖД-221 ИВАНОВМетоднаименьшихквадратов'); writeln('введите исходные данные:'); fori:=1 to5 do Begin write('x[',i:1,']='); {1,2,3,4,5} read(x[i]); write(' y[',i:1,']='); {1,<Ф>,<И>,<O>,5} read(y[i]); end; forp:=0 to4 do Begin c[p]:=0; d[p]:=0; fori:=1 to5 do Begin z:=stepen(x[i],p); c[p]:=c[p]+z; d[p]:=d[p]+z*y[i]; end; end; w:=c[0]*c[2]*c[4]+2*c[1]*c[2]*c[3]-c[2]*c[2]*c[2]-c[1]*c[1]*c[4]-c[0]*c[3]*c[3]; w0:=d[0]*c[2]*c[4]+d[1]*c[2]*c[3]+d[2]*c[1]*c[3]-d[2]*c[2]*c[2]-d[1]*c[1]*c[4]-d[0]*c[3]*c[3]; w1:=d[0]*c[2]*c[3]+d[1]*c[0]*c[4]+d[2]*c[1]*c[2]-d[1]*c[2]*c[2]-d[0]*c[1]*c[4]-d[2]*c[0]*c[3]; w2:=d[0]*c[1]*c[3]+d[1]*c[1]*c[2]+d[2]*c[0]*c[2]-d[0]*c[2]*c[2]-d[1]*c[0]*c[3]-d[2]*c[1]*c[1]; a0:=w0/w; a1:=w1/w; a2:=w2/w; writeln(' Р Е З У Л Ь Т А Т Ы'); writeln('P(x)=',a0:5:2,' +',a1:5:2,'*x +',a2:5:2,'*x:2'); write('x= '); {табулирование полинома для построения графика} fori:=1 to9 dowrite(0.5*(i+1):8:1); writeln; write('y= '); fori:=1 to9 do Begin w:=0.5*(i+1); z:=a0+a1*w+a2*w*w; write(z:8:2); end; writeln; er:=0; {вычислениеошибки} fori:=1 to5 do er:=er+(a0+a1*x[i]+a2*x[i]*x[i]-y[i])*(a0+a1*x[i]+a2*x[i]*x[i]-y[i]); er:=sqrt(er/5); writeln('СРЕДНЕКВАДРАТИЧЕСКАЯ ОШИБКА = ',er:7:5); readln; end. Окно вывода СЖД-221 ИВАНОВ Метод наименьших квадратов введите исходные данные: x[1]=1 y[1]=1 x[2]=2 y[2]=10 x[3]=3 y[3]=5 x[4]=4 y[4]=11 x[5]=5 y[5]=5 Р Е З У Л Ь Т А Т Ы P(x)=-5.80 + 9.04*x +-1.36*x*x x= 1.0 1.5 2.0 2.5 3.0 3.5 4.0 4.5 5.0 y= 1.89 4.71 6.86 8.33 9.11 9.23 8.66 7.41 5.49 СРЕДНЕКВАДРАТИЧЕСКАЯ ОШИБКА = 2.58125
В MATHCAD’е имеется программа полиномиального сглаживания данных (xi, yi) полиномом k-й степени А(х) = a + b·x + c·x2 + d·x3 + … + h·xk. При k = 1 полином является прямой линией, при k = 2 – параболой, при k = 3 – кубической параболой и т.д. Как правило, на практике применяется k< 5. Для построения полинома k-й степени необходимо наличие, по крайней мере, k + 1 точек данных. В программе сглаживание осуществляется комбинацией встроенной функции regressи полиномиальной интерполяции: regress(x,y,k) – вектор коэффициентов для построения сглаживающего полинома; interp(s,x,y,t) – результат полиномиальной интерполяции, гдеs = regress(x,y,k); х – вектор действительных данных аргумента, элементы которого расположены в порядке возрастания; у – вектор действительных данных значений того же размера; t – значение аргумента сглаживающего полинома.
Здесь на графике построены сглаживающие полиномы 1-й, 2-й и 6-й (интерполяционный) степени.
Задания
4.1. Построить линейную аппроксимацию таблично заданной функции: а) вручную (см. пример на стр. 3 ); б) на Паскале (стр. 4); в) в Маткаде (стр. 5).
4.2. Прибыль предприятия за некоторый период деятельности по годам приведена в таблице (см. ниже). Требуется (на Паскале и в Маткаде)(стр.5-7, 7-8): а) составить квадратичную зависимость прибыли по годам деятельности предприятия; б) определить ожидаемую прибыль для 8-го года деятельности.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 682. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
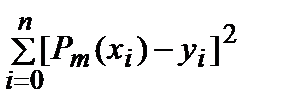 .(2)
.(2)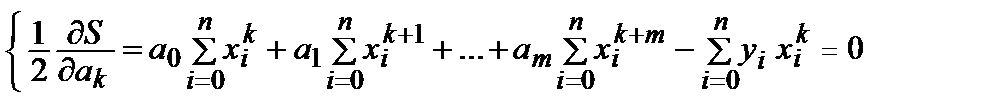 , (k = 0, 1, 2, … , m)(3)
, (k = 0, 1, 2, … , m)(3)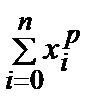 , dp =
, dp = 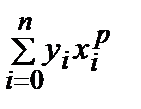 , запишем систему (3) в матричном виде
, запишем систему (3) в матричном виде 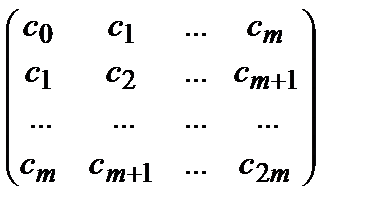 – матрица системы, а = {a0, a1, … , am}T – вектор неизвестных, d = {d0, d1, … , dm}T – вектор правых частей системы.
– матрица системы, а = {a0, a1, … , am}T – вектор неизвестных, d = {d0, d1, … , dm}T – вектор правых частей системы.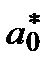 ,a1=
,a1= 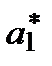 , … , am=
, … , am= 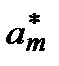 . Тогда полином
. Тогда полином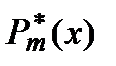 =
= 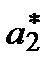 x2 + … +
x2 + … + 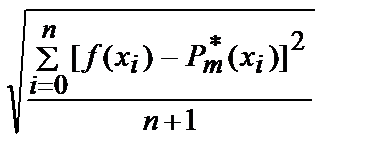 .
. 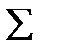
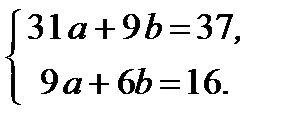 Решим ее с помощью
Решим ее с помощью 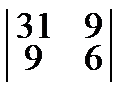 = 105, Δ1 =
= 105, Δ1 = 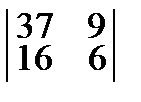 = 78, Δ2 =
= 78, Δ2 = 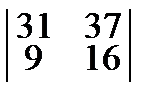 = 163,
= 163,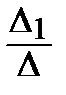 =
= 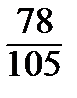 = 0,74, b =
= 0,74, b = 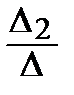 =
= 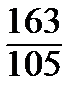 = 1,55.
= 1,55.















