
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Линейная регрессия общего видаСтр 1 из 2Следующая ⇒ Лекция 3: Статистическая обработка данных в системе Mathcad Аннотация:В лекции рассматриваются функции статической обработки встроенные в системе Mathcad. Особенности и недостатки данного программного пакета. Рассматривается возможность аппроксимации, представленные в системе Mathcad. Ключевые слова:Доверительная вероятность , Add, create, Data, editor, input, logic, math, net, OPEN, programmable logic device,rules, surface, target, XML, агрегация среднего значения, в диапазоне от х до у, генератор, двойной щелчок, жизненный цикл,зависимость между признаками, имя переменной, ключевое слово, логический, маршрутам, надежность, область определения,память, работам, связь, таблица, универсального множества, фазификация фактических данных, частотность, шкала,элементарные приемы, язык программирования Цель лекции: Ознакомиться с основными статистическими функциями в системе Mathcad. Уяснить предназначение этих функций. Понять для каких целей применяются данные функции. Mathcad — система компьютерной алгебры из класса систем автоматизированного проектирования, ориентированная на подготовку интерактивных документов с вычислениями и визуальным сопровождением, отличается легкостью использования и применения для коллективной работы. Широкий интерес к системе Mathcad привел к тому, что в России наконец-то появились книги по отдельным версиям. Система Mathcad была создана в 80-х годах в университете Станфорда (США). Современные версии для ПК готовит фирма MathSoft Application. Это универсальный · Математический интерфейс. · Есть мощная поддержка графики. · Возможен импорт графики из других программ. · Большое количество встроенных математических функций (сотни).  · Встроенные справочники по предметным областям. · Возможна анимация. · Символьная математика. Достоинство – программирование на языке математики. Недостатки: · Это интерпретатор. · Возможности программирования ограничены. Системы Mathcad пользуются огромной популярностью во всем мире благодаря удобным средствам подготовки документов, имеющих вид обычных статей или книг. В то же время оказывается, что эти средства вполне достаточны для решения подавляющего большинства задач по математике, физики и других направлений науки и техники. Mathcad является математически ориентированными универсальными системами. Помимо собственно вычислений они позволяют решать оформительские задачи. Они позволяют готовить статьи, книги, диссертации, научные отчеты, дипломные и курсовые проекты с доступным набором самых сложных математических формул и изысканным графическим представлением результатов. С самого первого своего появления системы класса Mathcad имели удобный пользовательский интерфейс – совокупность средств общения с пользователем в виде масштабируемых и перемещаемых окон, кнопок и иных элементов. У этой системы есть эффективные средства типовой научной графики, они просты в применении и интуитивно понятны. Словом, системы Mathcad ориентированы на массового пользователя – от ученика начальных классов до академика. Несмотря на то, что эта программа в основном ориентирована на пользователей-непрограммистов, Mathcad также используется в сложных проектах, чтобы визуализировать результаты математического моделирования, путем использования распределённых вычислений и традиционных языков программирования. Также Mathcad часто используется в крупных инженерных проектах, где большое значение имеет трассируемость и соответствие стандартам. Mathcad достаточно удобно использовать для обучения, вычислений и инженерных расчетов . Открытая архитектура приложения в сочетании с поддержкой технологий NET и XML позволяют легко интегрировать. Мы рассмотрим наиболее часто применяемые функции для статистических расчетов, которые встроены в программу. Функция RND(X). В статистических расчетах при моделировании различных физических процессов широко применяется встроенная функцияRND(X), инициализирующая генератор случайных чисел. Здесь Функции аппроксимации. Для представления физических закономерностей, а также при проведении научно-технических расчетов используются зависимости вида При кусочно-линейной интерполяции вычисления дополнительных точек выполняются по линейной зависимости. То есть, при линейной аппроксимации узловые точки соединяются отрезками прямых линий, для чего используется функция При сплайн-аппроксимации исходная функция заменяется отрезками кубических полиномов, проходящих через три смежные узловые точки. Коэффициенты этой функции рассчитываются таким образом, чтобы первая и вторая производные были непрерывными. Линия, описывающая сплайн-функцию, напоминает по форме гибкую линейку, закрепленную в узловых точках. Для осуществления сплайновой аппроксимации в Mathcad существуют четыре специальные встроенные функции: · · · Таким образом, сплайн-аппроксимация производится в два этапа: 1. Для выбранного способа приближения к узловым точкам вычисляется вектор вторых производных функции 2. С помощью функции Функции регрессии. Широко распространенной задачей обработки данных является представление их совокупности некоторой функцией Известны: 1. Линейная регрессия (прямая линия), 2. Полиномиальная регрессия (полином), 3. Линейная регрессия общего вида (линейная сумма произвольных функций), 4. Нелинейная регрессия общего вида (произвольная функция) Линейная регрессия При линейной регрессии функция Для проведения линейной регрессии в Mathcad имеются ряд встроенных функций: · · · где Полиномиальная регрессия При полиномиальной регрессии функция
Для реализации полиномиальной регрессии имеется встроенная функция Линейная регрессия общего вида При линейной регрессии общего вида функция
Функция регрессии является линейной комбинацией нескольких функций Для реализации линейной регрессии общего вида используется функция |
||||||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 259. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 задаётся как ранжированная переменная и определяет число случайных чисел. Например, для получения десяти случайных чисел следует задать интервал
задаётся как ранжированная переменная и определяет число случайных чисел. Например, для получения десяти случайных чисел следует задать интервал 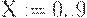 .
.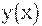 , но число точек этих зависимостей ограничено. При этом возникает задача приближенного вычисления значений функций в промежутках между узловыми точками и за их пределами. Такая задача решается аппроксимацией исходной зависимости, то есть ее подменой какой-либо достаточно простой функцией. В системе Mathcad предоставляется возможность аппроксимации двумя типами функций: кусочно-линейной и сплайновой.
, но число точек этих зависимостей ограничено. При этом возникает задача приближенного вычисления значений функций в промежутках между узловыми точками и за их пределами. Такая задача решается аппроксимацией исходной зависимости, то есть ее подменой какой-либо достаточно простой функцией. В системе Mathcad предоставляется возможность аппроксимации двумя типами функций: кусочно-линейной и сплайновой. – линейная интерполяция,где
– линейная интерполяция,где  ,
,  – векторы координат узловых точек, а x – заданный аргумент. При небольшом числе узловых точек линейная интерполяция оказывается довольно грубой. Даже первая производная функция аппроксимации получается с резкими скачками в узловых точках. Поэтому применяют функцию сплайн-аппраксимации.
– векторы координат узловых точек, а x – заданный аргумент. При небольшом числе узловых точек линейная интерполяция оказывается довольно грубой. Даже первая производная функция аппроксимации получается с резкими скачками в узловых точках. Поэтому применяют функцию сплайн-аппраксимации. – возвращает вектор
– возвращает вектор  вторых производных при приближении в опорных точках к параболической кривой
вторых производных при приближении в опорных точках к параболической кривой – возвращает вектор
– возвращает вектор  – возвращает значение
– возвращает значение  для заданных
для заданных  и заданного значения
и заданного значения 
 , заданной векторами
, заданной векторами  ее значений с помощью одной из функций cspline, pspline или lspline.
ее значений с помощью одной из функций cspline, pspline или lspline. вычисляется значения
вычисляется значения  и описывает отрезок прямой.
и описывает отрезок прямой. – функция корреляции. Возвращает скаляр – коэффициент корреляции векторов
– функция корреляции. Возвращает скаляр – коэффициент корреляции векторов  – возвращает параметр
– возвращает параметр  - смещение линии регрессии векторов
- смещение линии регрессии векторов  ) – возвращает значение параметра
) – возвращает значение параметра  - наклон линии регрессии векторов
- наклон линии регрессии векторов 
 , которая возвращаетвектор
, которая возвращаетвектор  , содержащий коэффициенты полинома n–й степени. Эти коэффициенты вычисляются по всей совокупности заданных точек, т. е. глобально. Полученный полином наилучшим образом приближается к "облаку" точек с координатами, хранящимися в векторах
, содержащий коэффициенты полинома n–й степени. Эти коэффициенты вычисляются по всей совокупности заданных точек, т. е. глобально. Полученный полином наилучшим образом приближается к "облаку" точек с координатами, хранящимися в векторах 
 причем сами эти функции могут быть и нелинейными, что резко расширяет возможности такой аппроксимации и распространяет ее на нелинейные функции.
причем сами эти функции могут быть и нелинейными, что резко расширяет возможности такой аппроксимации и распространяет ее на нелинейные функции. которая возвращаетвектор коэффициентов К линейной регрессии общего вида, при котором коэффициент корреляции"облака" исходных точек и функции
которая возвращаетвектор коэффициентов К линейной регрессии общего вида, при котором коэффициент корреляции"облака" исходных точек и функции  должен содержать функции
должен содержать функции