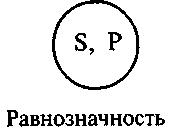
Виды отношений между именами

Имена находятся в различных отношениях друг к другу. Между объемами двух произвольных имен, которые есть какой-то смысл сопоставлять друг с другом, имеет место одно и только одно из следующих отношений: равнозначность, пересечение, подчинение (два варианта) и исключение.

Равнозначными являются два имени, объемы которых полностью совпадают. Иными словами, равнозначные имена отсылают к одному и тому же классу предметов, но делают это разными способами.

Равнозначны, к примеру, имена «квадрат» и «равносторонний прямоугольник»: каждый квадрат является равносторонним прямоугольником, и наоборот.

Равнозначность означает совпадение объемов двух имен, но не их содержаний. Например, объемы имен «сын» и «внук» совпадают (каждый сын есть чей-то внук и каждый внук – чей-то сын), но содержания их различны.

Отношения между объемами имен можно геометрически наглядно представить с помощью круговых схем. Они называются по имени математика XVIII в. Л. Эйлера «кругами Эйлера». Каждая точка круга представляет один предмет, входящий в объем рассматриваемого имени. Точки вне круга представляют предметы, не подпадающие под это имя.

Отношение между двумя равнозначными именами изображается в виде двух полностью совпадающих кругов.

В отношении пересечения находятся два имени, объемы которых частично совпадают.

Пересекаются, в частности, объемы имен «летчик» и «космонавт»: некоторые летчики являются космонавтами (они представлены заштрихованной частью кругов), есть летчики, не являющиеся космонавтами, и есть космонавты, не являющиеся летчиками.

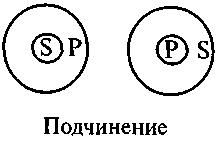
В отношении подчинения находятся имена, объем одного из которых полностью входит в объем другого.

В отношении подчинения находятся, к примеру, имена «треугольник» и «прямоугольный треугольник»: каждый прямоугольный треугольник является треугольником, но не каждый треугольник прямоугольный.

В этом же отношении находятся имена «дедушка» и «внук»: каждый дедушка есть чей-то внук, но не каждый внук является дедушкой. «Внук» – подчиняющее имя, «дедушка» – подчиненное.

Если в отношении подчинения находятся общие имена, то подчиняющее имя называется родом, а подчиненное – видом. Имя «треугольник» есть род для вида «прямоугольный треугольник», а имя «внук» – род для вида «дедушка».

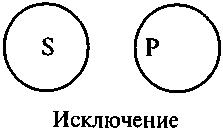
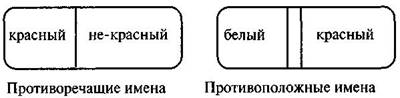
В отношении исключения находятся имена, объемы которых полностью исключают друг друга.

Исключают друг друга имена «трапеция» и «пятиугольник», «человек» и «планета», «белое» и «красное» и т.п.

Можно выделить два интересных вида исключения:

1. Исключающие объемы дополняют друг друга так, что в сумме дают весь объем рода, видами которого они являются. Имена, объемы которых исключают друг друга, исчерпывая объем родового понятия, называются противоречащими.

Противоречащими являются, например, имена «умелый» и «неумелый», «стойкий» и «нестойкий», «красивый» и «некрасивый» и т.п. Противоречат друг другу также имена «простое число» и «число, не являющееся простым», исчерпывающие объем родового имени «натуральное число», имена «красный» и «не являющийся красным», исчерпывающие объем родового имени «предмет, имеющий цвет», и т.п.

2. Исключающие имена составляют в сумме только часть объема того рода, видами которого они являются. Имена, объемы которых исключают друг друга, не исчерпывая объем родового имени, называются противоположными.

К противоположным относятся, в частности, имена «простое число» и «четное число», не исчерпывающие объема родового имени «натуральное число», имена «красный» и «белый», не исчерпывающие объема родового имени «предмет, имеющий цвет» и т.п.

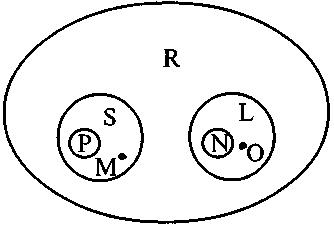
Круговые схемы могут применяться для одновременного представления объемных отношений более чем двух имен. Такова, к примеру, приводимая на рисунке схема, представляющая отношения между объемами имен: «планета» (S), «планета Солнечной системы» (Р), «Земля» (M), «спутник» (L), «искусственный спутник» (N), «Луна» (О) и «небесное тело» (R). Согласно этой схеме существуют, в частности, небесные тела, не являющиеся ни планетами, ни их спутниками, планеты, не входящие в Солнечную систему, спутники, не являющиеся искусственными, и т.д. Объемы единичных имен представляются точками.

Определение

Определение – логическая операция, раскрывающая содержание имени. Определить имя – значит указать, какие признаки входят в его содержание.

Определяя, например, манометр, мы указываем, что это, во-первых, прибор, и, во-вторых, именно тот, с помощью которого измеряется давление. Давая определение имени «графомания», мы говорим, что это болезненное пристрастие к писанию, к многословному, пустому, бесполезному сочинительству.

Важность определений подчеркивал еще Сократ, говоривший, что он продолжает дело своей матери, акушерки, и помогает родиться истине в споре. Анализируя вместе со своими оппонентами различные случаи употребления конкретного понятия, он стремился прийти, в конце концов, к его прояснению и определению.

Задачи определения

Определение решает две задачи. Оно отличает и отграничивает определяемый предмет от всех иных. Скажем, определение манометра позволяет однозначно отграничить манометры от всех предметов, не являющихся приборами, и отделить манометры по присущим только им признакам от всех иных приборов. Далее, определение раскрывает сущность определяемых предметов, указывает те их основные признаки, без которых они не способны существовать и от которых в значительной мере зависят все иные их признаки.

С этой второй задачей как раз и связаны основные трудности определения конкретных имен.

Дать хорошее определение – значит раскрыть сущность определяемого объекта. Но сущность, как правило, не лежит на поверхности. Кроме того, за сущностью первого уровня всегда скрывается более глубокая сущность второго уровня, за той – сущность третьего уровня и так до бесконечности. Эта возможность неограниченного углубления в сущность даже простого объекта делает понятными те трудности, которые встают на пути определения, и объясняет, почему определения, казалось бы, одних и тех же вещей меняются с течением времени. Углубление знаний об этих вещах ведет к изменению представлений об их сущности, а значит, и их определений.

Необходимо также учитывать известную относительность сущности: существенное для одной цели может оказаться второстепенным с точки зрения другой цели.

Скажем, в геометрии для доказательства разных теорем могут использоваться разные, не совпадающие между собой определения понятия «линия». И вряд ли можно сказать, что одно из них раскрывает более глубокую сущность этого понятия, чем все остальные.

Писатель И. Рат-Вег в своей «Комедии книги» упоминает некоего старого автора, чрезвычайно не любившего театр. Отношение к театру этот автор считал настолько важным, что определял через него все остальное. Рай, писал он, это место, где нет театра, дьявол – изобретатель театра и танцев, короли – люди, которым особенно позорно ходить в театр и покровительствовать актерам, и т.п. Разумеется, эти определения поверхностны со всех точек зрения. Со всех, кроме одной: тому, кто всерьез считает театр источником всех зол и бед, существующих в мире, определения могут казаться схватывающими суть дела.

Определение может быть более глубоким и менее глубоким, и его глубина зависит прежде всего от уровня знаний об определяемом предмете. Чем лучше, глубже мы знаем предмет, тем больше вероятность, что нам удастся найти хорошее его определение.