
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Распространение метода формализациив процессе изучения различных теорий. ⇐ ПредыдущаяСтр 3 из 3 Формализация (от лат. forma - вид, образ) - отображение объектов некоторой предметной области с помощью символов к.-л. языка. Простейший вид Ф. - прямая репрезентация (обозначение, именование, описание) объектов с помощью терминов. Такая «дескриптивная» Ф. лежит в основе всех др. типов Ф., среди которых прежде всего различают естественную и научную Ф. Естественная Ф. представляет собой отображение объектов с помощью того или иного естественного языка; научная Ф. - с помощью соответствующего формального языка. В процессе научной Ф., с одной стороны, осуществляется более точное и компактное отображение конкретных свойств и отношений, характеризующих ту или иную область исследования, а с др. стороны, используются дополнительные символические средства, позволяющие путем чисто синтаксических (формальных) преобразований получать новое знание об исследуемой предметной области.(Кроме терминов, к числу символических средств относятся переменные, формулы, метаформулы, правила преобразования формул и метаформул, а также различного рода вспомогательные символы (скобки, запятые и т.п.)). В качестве объекта логической Ф. может выступать любое обыденное или научное знание.. Дедуктивная Ф. позволяет уточнить и систематизировать различные содержательные представления, сформулировать новые проблемы и возможные пути их решения. Методы дедуктивной Ф. все шире применяются в различных областях естественно-научного и гуманитарного знания. Особенно важное практическое применение методы логической Ф. имеют в информатике, в области компьютерного моделирования познавательных процессов человека.  Дополнение! Структура записи теорем!
Т.Геделя о неполноте.Всякая ω-непротиворечивая и адекватная формальная арифметика не является полной. Д-во. Мн-во Q натуральных чисел, которое перечислимо, но неразрешимо. ПеридикатР(х, у) такой, что Q={x:( Представимость предиката Р(х, у) в формальной арифметике означает, что найдется такая формула F(x, у) этой теории, содержащая лишь две свободных предметных переменных, что для каждой пары натуральных чисел (а, b), для которой λ [Р(а, b)] = 1, имеет место теорема: ├F{a*, b*),а для каждой пары натуральных чисел (а, b), для к-ой λ [Р(а, b)] = 0, имеет место теорема: ├ F(a*,b*). Применим к формуле F(x, у) квантор общности по переменной у. Получим формулу с единственной свободной предметной переменной х: G(x) = ( Покажем, что Q={x:├G(x*)}.Предположим, что mЄQ. Тогда (согласно (*)) найдется такое натуральное n, что выск-иеР(m, n) истинно. Следовательно, имеет место теорема: ├ F(m*, n*). Поскольку наша формальная арифметика, кроме того, ω-непротиворечива, то, ввиду наличия в ней последней теоремы, должно существовать такое натуральное число n0, что ф-ла F(m*,n0*) не является теоремой этой арифметики. А раз так, то высказывание Р(m, n0) истинно. По определению (*) мн-ва Q, это означает, что mЄQ. Таким образом, {x :├G(x*)} Итак, равенство (**) доказано.
|
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 559. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
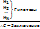 – Умозаключение.
– Умозаключение.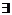 y)(λ[P(x,y)] = l)}. (*)
y)(λ[P(x,y)] = l)}. (*) Q.
Q.