
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Дедуктивынй характер математики.Стр 1 из 3Следующая ⇒ Математика представляет собой совокупность доказательств. Основное средство доказательства — дедукция (от лат. deductio — выведение), что означает вывод по правилам логики, то есть построение такой цепи умозаключений (рассуждения), звенья которой (высказывания) связаны отношением логического следования. В широком смысле дедукция — такая форма мышления, когда новая мысль выводится по одному из законов логики из некоторых данных мыслей (посылок), которые могут быть либо аксиомами, либо ранее доказанными утверждениями. Последняя мысль рассуждения называется выводом или заключением. Как правило, математические доказательства являются дедуктивными умозаключениями, и, следовательно, математические теории имеют дедуктивный характер. Логика (греч. logos,–понятие, рассуждение, разум.) – это наука, изучающая формы и законы мышления, закономерности мыслительного процесса.Предметом математической логики служат рассуждения,при изучении которых она пользуется математическими методами. Математическая теория содержит утверждения (аксиомы и теоремы).Для уточнения понятий «утверждение» и «доказательство» вводятся их формальные аналоги. Утверждения, записанные на формальных языках, называют формулами, чтобы отличить их от предложений естественных языков. Формальный аналог понятия «доказательство» - понятие вывода (доказательства, записанного на формальном языке). Формальным аналогом понятия «теорема» является понятие «выводимая формула» (т.е. формула, имеющая вывод). Формальный язык вместе с правилами построения выводов называется формальной системой, которая должна быть как можно более похожей на естественный язык. Основным предметом математической логики, ТО, является построение и изучение формальных систем  2. Потом!
3. Высказывание –обычно всякое повествовательное предложение, утверждающее что-либо о чем-либо, истинность или ложность (их логическое значение) которого в данных условиях места и времени мы можем определить. Высказывание, представляющее собой одно утверждение, принято называть простым или элементарным. Высказывания, которые получаются из элементарных с помощью грамматических связок «не», «и», «или», «если .... то ...», «тогда и только тогда», принято называть сложными или составными. Операции:Отрицанием высказывания х называется новое высказывание, которое является истинным, если высказывание х ложно, и ложным, если высказывание х истинно.
Дизъюнкцией(логическим сложением – Исключающая дизъюнкция( Импликацией двух высказываний Эквивалентностью Штрих Шеффера(!)— это отрицание конъюнкции. Стрелка Пирса( Наиболее приоритетна функция отрицания. Затем идет конъюнкция, после нее – дизъюнкция. Все другие функции имеют равный приоритет, меньший, чем у дизъюнкции.
4. Всякое сложное высказывание, которое может быть получено из элементарных высказываний посредством применения логических операций отрицания, конъюнкции, дизъюнкции, импликации и эквиваленции, называется формулой алгебры логики. Базовыми понятиями логики высказываний являются пропозициональная переменная — переменная, значением которой может быть логическое высказывание, — и (пропозициональная) формула, определяемая индуктивно следующим образом: //Метод математической индукции: проверяется истинность утверждения с номером 1 — база (базис) индукции, а затем доказывается, что, если верно утверждение с номером n, то верно и следующее утверждение с номером n + 1 — шаг индукции, или индукционный переход.// 1)IF P — пропозициональная переменная, то P — формула. 2)IF A — формула, то— ¬Aформула. 3)IF A и B — формулы, то 4)Других соглашений нет. Все формулы алгебры логики можно разделить на нейтральные, или выполнимые – принимающие как истинное, так и ложное значения; тождественно истинные формулы (или тавтологии) – принимающие истинные значения при любых значениях переменных; тождественно ложные формулы (или противоречие)– принимающие ложные значения при любых оценках переменных. Основной задачей логики высказываний является установление истинностного значения формулы, если дана оценка (т.е. определены истинностные значения входящих в неё переменных). Множество истинностных значений {0;1}. Существует два способа определения истинного значения формулы. Первый – с помощью таблиц истинности, а второй – путём приведения формул к нормальной форме. Формула имеет нормальную форму, если в ней отсутствуют знаки эквиваленции, импликации, двойного отрицания и др., при этом знаки отрицания находятся только при переменных.
5. Две формулы алгебры логики А и В называются равносильными, если они принимают одинаковые логические значения на любом наборе значений входящих в формулы элементарных высказываний (А Отношение равносильности между формулами алгебры высказываний: 1)Рефлексивно F≡H 2)Симметрично: еслиf1≡F2, То f2≡f1 3)Транзитивно: если f1≡F2 и f1≡F3 то f1≡F3 Равносильные преобразования формул: используя законы можно от одной формулы переходить к равносильной ей формуле. Такой переход называетсяРавносильным преобразованием формулы. Равносильные преобразования используются для доказательства равносильностей, для приведения формул к заданному виду, для упрощения формул. Формула А считается проще равносильной ей формулы В, если она содержит меньше букв, меньше логических операций. Законы: З. идемпотентности: З. двойного отрицания: Переменная и ее отрицание: З. противоречия: Операции с константами: З. исключающего третьего: З. склеивания: З. поглощения:x Эквивалентность операций:
З. Де-Моргана: Коммутативность конъюнкции и дизъюнкции:
Ассоциативность
Дистрибутивность Дистрибутивность Дистрибутивность
7. Тавтология –тождественно истинное высказывание Логический закон логики высказываний– это тавтология данной логики. Иными словами, множество законов логики высказываний и множество ее тавтологий совпадают: каждый закон есть тавтология, и каждая тавтология есть закон. Это означает, что для установления того, является ли некоторая формула законом логики высказываний, достаточно с помощью таблиц истинности убедиться, является ли эта формула тавтологией. Т.О., логический закон можно определить как выражение, содержащее только логические константы и переменные и являющееся истинным в любой (непустой) области объектов. Законы контрапозиции говорят о перемене позиций высказываний с помощью отрицания: из условного высказывания "если есть первое, то есть второе" вытекает "если нет второго, то нет и первого", и наоборот: (А → В) → (~ В → ~ А) или (~ В → ~ А) → (А → В) ("Если есть следствие, то есть и причина" →"Если нет причины, нет и следствия") Закон исключенного третьего устанавливает связь между противоречащими друг другу высказываниями. Он утверждает: из двух противоречащих высказываний одно является истинным: A v ~ A ("Личинки мух имеют голову или не имеют ее" – дело обстоит так, как говорится в рассматриваемом высказывании, или так, как говорится в его отрицании, и никакой третьей возможности нет). Полный закон двойного отрицания: Закон двойного отрицания:отрицание отрицания дает утверждение: Обратный закон двойного отрицания: утверждение влечет свое двойное отрицание. Редукция к абсурду (приведение к нелепости) –это рассуждение, показывающее ошибочность какого-то положения путем выведения из него абсурда, т.е. логического противоречия. (А → В) ("Треугольник – это окружность" →(треугольник имеет углы (как ▲)иу него нет углов(как у ○)) => верным является не исходное высказывание, а его отрицание "Треугольник не является окружностью") Частный закон :(А → ~ А) → ~ А ("Всякое правило имеет исключения" само является правилом, из него вытекает "Есть правила, не имеющие исключений" → последнее высказывание истинно) Закон противоречия: высказывание и его отрицание не могут быть вместе истинными: Закон тождества: если высказывание истинно, то оно истинно: А → А Модус Поненс (правило отделения): ((“Учеловека грипп→ он болен” и “У человека грипп”)→“Человек болен”) Модус Толленс(принцип фальсификации): ((“гелий – металл→ он электропроводен” и “Гелий неэлектропроводен”)→“Гелий – не металл”.) Закон транзитивности: когда верно, что если первое, то второе, и если второе, то третье, то верно также, что если первое, то третье.
Еще в 5 билете. Теорема дедукции, доказанная Эрбраном,- по-видимому самый эффективный прием в классическом исчислении высказываний (КИВ). Хотя она и называется "теоремой" дедукции - это не теорема КИВ, а метод, который применяется для их доказательства. То есть, как говорят, метатеорема. // Метатеорема дедукции (МТД): Где Г – вывод (конечная последовательность В1..Вn таких, что для каждого iϵ[1;n] Вi есть какая-либо аксиома ИВ, либо непосредственное следствие предыдущих правил, взятых как посылки правила “modusponens” (mp: //Секвенция. Если Г –конечное множество формул (возможно пустое) из всех формул ИВ (FLИВ), аА – какая-то формула из FLИВ, то выражениевида Доказательство (индукция): Пусть В1..Вn(1!)–вывод формулы B из гипотез Г, А. База индукции (n=1): тогда (1!) состоит только из 1 формулы В. Возможны вар-ты: а)If В – аксиома, то имеем вывод: //расширение гипотез: Вывод:
б)IfB – одна из формул Г, то: в)If В является формулой А, то: Индуктивное предположение: Будем предполагать, что МТД доказана для всех секвенций Индуктивный шаг: Пусть секвенция Возможны варианты: а)Bn+1– аксиома; б)Bn+1– одна из формул Г в)Bn+1– является формулой А //Что рассматривается аналогично ранее рассмотренному.// г)Bn+1 – получаетсяизBiиBj (i,jϵ[1;n]) по правилу mp Т.к. i,j≤n, то для секвенций
//Аксиома L2 ИВ(самодистрибутивность ЧТД. 15. Предикат –предложение, определенное на множестве М1..Mn, содержащее n переменных (х1..хn) и превращающееся в высказывание при подстановке. P(x1..xn) – n-местный предикат; x1..xn – предметные переменные; элементы множеств М1..Mn – конкретные предметы. Формулами ЛП являются: 1)предметные переменные: x,y,z, xi, yi, xi,… (i Є N); 2)нульместные предикатные переменные P,Q,R,Pi,Qi,Ri, (i Є N); 3)любой n-местный предикат P(x1,x2,…,xn), Q(x1,x2,…,xn), R(x1,x2,…,xn),…; 4)IF F, G- формулы, не содержащие предметных переменных, которые связаны квантором в одной формуле и свободны в другой, то выражения 5)если F формула, а x- предметная переменная, входящая свободно в F, то выражения 6)других формул нет. Множество истинности предикатовРх1..хn, заданных на множестве М1..Mn– совокупность всех упорядоченных М-систем, в которых а1ϵ М1.. аnϵMn , таких что данный предикат обращается в истину; обозначается Р+. (Р+={(a1..an): λ(P(a1..an))=1} Предикат: 1)тождественно истинен, тогда и только тогда, когда Р+=M1*M2*…*Mn 2)Тождественно ложен …, когда 3)Выполним …, когда 4)Опровержим, когда Две формулы логики предикатов А и В равносильны на области М,если они принимают одинаковые логические значения при всех значениях входящих в них переменных, отнесенных к области М. Две формулы логики предикатов А и В наз-сяравносильными, если они равносильны на всякой области. #, пусть А(х) и В(х) – переменные предикаты, тогда Т. Т. Говорят, что формула логики предикатов имеет нормальную форму, если она содержит только операции конъюнкции, дизъюнкции и кванторные операции, а операция отрицания отнесена к элементарным формулам Если в алгебре высказываний приняты две нормальные формы (ДНФ - дизъюнктивная и КНФ -конъюнктивная), то в алгебре предикатов - одна предварённая нормальная форма (ПНФ), суть которой сводится к разделению формулы на две части: кванторнуюи безкванторную:
16. ФормулаА логики предикатов называется выполнимой в области М, если существуют значения переменных, входящих в эту формулу и отнесенных к области М, при которых формула А принимает истинные значения. Формула А называется выполнимой, если существует область, на которой эта формула выполнима. Формула А называется тождественно истинной/ложной в области М, если она принимает истинные/ложные значения для всех значений переменных, входящих в эту формулу и отнесенных к этой области. Формула А называется общезначимой, если она тождественно истинная во всякой области. Общезначимую формулу называют логическим законом. Из приведенных определений следует: 1.Если формула А общезначима, то она и выполнима на всякой области. 2.Если формула А тождественно истинна в области М, то она выполнима в этой области. 3. Если формула А тождественно ложна в области М, то она невыполнима в этой области. 4. Если формула А невыполнима, то она тождественно ложна в любой области. В связи с данными определениями выделяются два класса формул логики предикатов: выполнимых и невыполнимых формул. Следующие теоремы устанавливают связь между общезначимостью и выполнимостью формул логики предикатов. Т1.Для того, чтобы формула А была общезначима, необходимо и достаточно, чтобы ее отрицание было невыполнимо. Т2. Для того, чтобы формула А была выполнимой, необходимо и достаточно, чтобы формулабыла необщезначима
17. Проблема разрешимости в ЛП ставится так же, как и в алгебре логики: существуют ли алгоритмы, позволяющие для любой формулы А логики предикатов установить, к какому типу (классу) она относится, т.е. является ли она общезначимой, выполнимой или тождественно ложной (невыполнимой). В отличие от алгебры логики, в ЛП не применим метод перебора всех вариантов значений переменных, входящих в формулу, так как таких вариантов может быть бесконечное множество. Решения: 1)На конечных множествах – вместо предикатных переменных можно подставить конкретные предикаты, определенные на этих конечных множествах. Операции квантификации в током случае сводятся к конъюнкции и дизъюнкции, что сводит проблему разрешимости к методу определения общезначимости и выполнимости некоторой формулы алгебры высказываний.(# таблица истинности; 2)Влияние мощности множества (выполнимость) – по выполнимости формулы на некотороммнож-ве нельзя судить о выполнимости формулы на его подмножествах. Т.Если некоторая формула ЛП выполнима в каком-н. множ-ве, то она выполнима так же и в каждом множ-ве с большим числом элементов (> мощном) Далее, можно свести проблему разрешимости ЛП к проблеме разрешимости формул некоторых специальных видов: Любую форму ЛП можно свести к предваренной нормальной форма, которую можно свести к предваренной нормальной форме Сколема (кванторная приставка имеет вид: 3)Формула только с одноместными предикатными переменными – в этом случае проблема сводится к проблеме разрешения выполн. иобщезн. формулы на конечном множ-вес помощью Т.: Если формула ЛП, содержащая только одноместные предикатные переменные, выполнима, то она выполнима на конечном множестве, содержащем не более 2n элементов, где n – число различных предикатных переменных, входящих в рассматриваемую формулу. Следстивие: если замкнутая формула F(P1…Pn), в которую входят только одноместные предикатные переменные P1…Pn, тождественно истинна на множестве из 2n элементов, то она общезначима. 4)Влияние мощности множества (общезначимость) Теорема Лёвенгейма: если формула истинна в счетно-бесконечной области, то она общезначима (Бесконечное множество считается счётным, если можно установить одно-однозначное соответствие между его элементами и натуральными числами). Но снова существует проблема перехода от бесконечных множеств к конечным или обратно, а так же от одного конечного к другому, с большим числом элементов. 5) Решение проблемы для Т. Т. Итого: проблема трудна и отнюдь не решена.
18. Язык логики предикатов удобен для записи математических предложений и определений. Он дает возможность выражать логические связи между понятиями, записывать определения, теоремы и доказательства. Приведем несколько примеров таких записей. Пример 1. Определение непрерывности функции в точке. Функция f(x), определенная на множестве Е, непрерывная в точке х0ÎЕ, если ("e)>0 существует d>0 ("xÎE(P(e,d,x))), где P(e,d,x)=(0<|x-x0|<d"|f(x)-f(x0)|<e) Пример 2. Определение возрастающей функции. Функция f(x) определенная на множестве Е возрастает на этом множестве, Если "х1ÎЕ"х2ÎЕ(х1<x2Þf(x1)<f(x2)). Здесь использован двуместный предикат. Пусть дано некоторое математическое утверждение А. Ему противоположно Для построения противоположного утверждения к утверждению, заданному формулой логики предикатов, содержащей все кванторы впереди, необходимо заменить все кванторы на противоположные и взять отрицание от предиката, стоящего под знаком кванторов. Определение неограниченной функции (равносильные преобраз-я): Формальная система отражает синтаксические аспекты математич. теории, т.е. отражает процесс переноса наших мыслей о математич. объектах в отображающие их записи с помощью спец. символов. В теорию первого порядка входят: Язык первого порядка.Чтобы задать язык первого порядка нужно определить символы и формулы языка. Символами языка первого порядка является: 1. переменные 2. n-арные функциональные символы 3. символы Следующие символы называются логическими символами: переменные, знаки Функциональные и предикатные символы, отличные от знака =, являются нелогическими символами. Они зависят от теории. Логические символы одни и те же во всех теориях. У каждой теории свой, индивидуальный набор функциональных и предикатных символов, отражающих понятия данной теории. Число n-арных функциональных и предикатных символов для данногоn произвольно и в, частности, может равняться 0. Однако среди предикатных символов должен быть символ =. Переменные служат для обозначения произвольных объектов теории T. #, x может означать в арифметике число, в геометрии вектор, пря- мую и т.п. Терм –это: 1. переменная; 2. если u1, . . .un—термы и f —n-арный функциональный символ, то fu1u2 . . .un—терм; 3. то, что выражение является термом устанавливается несколькими применениями правил 1 и 2. Скобки и запятые отсутствуют среди символов теории первого порядка и поэтому их нет в определении терма, но для наглядности можно употреблять запись Атомной формулой называется выражение вида p – n-арный предикатный символ, Формула –это: 1. Атомная формула; 2. Если A и B - произвольные формулы, то ¬A, A∨B- формулы. 3. Если A - формула, то 4. Выражение является формулой тогда и только тогда, когда оно получено несколькими применениями правил 1-3. (# нет квантора Задание символов и формул, полностью определяет язык 1-го порядка. Аксиомы теории первого порядка.делятся на два вида логические и нелогические. Логические аксиомы — законы логики, которые мы используем в математике. В теории первого порядка правила логического вывода строго зафиксированы. В нелогических аксиомах (специальных) отражают свойства объектов, рассматриваемых в теории (#, свойства сложения, умножения и отношения Операция подстановки. Для формулировки аксиом нам необходимо понятие подстановки вместо переменной произвольного терма. Эта подстановка может осуществляться в терме или в формуле. связанной и свободной переменной в формуле. Опр.Вхождение переменной x в формулу A называется связанным, если оно содержится в некоторой части формулы A следующего вида ∃xB. В противном случае данное вхождениеназывается свободным. Опр. Переменная x называется свободнойв A, если в A есть свободное вхождение x; переменная x называется связанной в A, если в A есть связанное вхождение x. Т.Результат замены Т. Результат замены Логические аксиомы имеют следующий вид, где A — произвольная формула, a—терм: пропозициональная аксиома аксиома равенства (два вида)
аксиома подстановки аксиома тождества
20. Теории первого порядка рассматриваются в виде формальных систем. Третьей частью формальной системы являются ее правила вывода, которые служат для получения теорем. В этих правилах отражены законы логики, которые мы применяем в математическом доказательстве. Имеется пять правил вывода. Четыре из них заимствованы из исчисления высказываний и одно новое. Правило расширения
Правило сокращения
Правило ассоциативности
Правило сечения.
Правило ∃введения.
− где x не является свободной переменной вB. Теория доказательств –это раздел математической логики, представляющий доказательства в виде формальных математических объектов, осуществляя их анализ с помощью математических методов. Доказательства обычно представляются в виде индуктивно определённых структур данных, таких как списки и деревья, созданных в соответствии с аксиомами и правилами вывода формальных систем. Теорема дедукции: Доказательство (индукция): Пусть В1,…,Bi,…,Bn есть вывод формулы В= Bn из гипотез Г, А и Δ1(Вi) – соответствующее этому множеству подмножество формул. Индукцией по длине вывода n будем строить вывод формулы Рассмотрим только случай, характерный для ИПФ (исчисление формул и предикатов): формула По индуктивному предположению существует вывод из гипотез Г (часть (1!) до Bi)… Рассмотрим 2 случая: Сл. 1: Добавив к (1i!) несколько формул, получим вывод секвенции
Сл. 2: Добавив к выводу (3!) две формулы, получим вывод
ЧТД. 22. Непротиворечивость –важнейшее свойство аксиоматических теорий и важнейшее требование, к ним предъявляемое. Опр.Аксиоматич. теория наз-сянепротиворечивой, если ни для какого утверждения А, сформулированного в терминах этой теории, само утверждение А и его отрицание не могут быть одновременно теоремами этой теории. Если для некоторого утверждения А теории оба утверждения А и Обобщенно можно сказать, что аксиоматическая теория наз-сяполной,если она содержит достаточное для какой-либо цели количество теорем. Это понятие относительное. Опр.Аксиоматическая теория (АТ)называется абсолютно полной, если ее средств достаточно для доказательства или опровержения любого утверждения, сформулированного в рамках данной теории. Смысл абсолютной полноты в том, чтобы она давала возможность не прибегать к дополнительным аксиомам для доказательства. Разрешающим методом для формальной системы F называется такой метод, с помощью которого для любой данной формулы A из F мы можем за конечное число шагов решить, будет ли A теоремой системы F или нет. Проблема разрешимости состоит в следующем: найти такой метод (алгоритм) или доказать, что его не существует. 23. Т. адекватностиисчисления предикатов и формул (ИПФ) 1. Предложение А выводимо в ИПФ тогда и только тогда, когда оно является тождественно истинным. 2. Для конкретного множ-ва Г секвенция Т. о непротиворечивости ИПФ. ИПФ непротиворечиво. Доказательство следует из того факта, что выводимыми предложениями являются лишь тождественно истинные. Что следует из теоремы адекваности
25. Интерпретация формулы A –отображение множества пропозициональных переменных, входящих в эту формулу, в множество {И,Л}. Интерпретация ставит в соответствие каждой пропозициональной переменной ее истинностное значение. Если выписан набор (последовательность) всех пропозициональных переменных формулы A, то для задания интерпретации достаточно выписать набор значений соответствующих пропозициональных переменных. Определим индуктивно истинностное значение формулы A в выбранной интерпретации: 1) истинностное значение формулы, являющейся пропозициональной переменной, есть истинностное значение этой переменной; 2) истинностное значение формулы вычисляется по истинностным значениям ее подформул следующим образом. Всякую сложную формулу C можно представить только в одном из видов: Для вычисления истинностных значений формулы во всех ее интерпретациях, удобно составить таблицу, содержащую всевозможные интерпретации формулы и cоответствующие этим интерпретациям значения формулы. Ее называют истинностной таблицей формулы (или просто таблицей истинности). Чтобы безошибочно выписать все интерпретации формулы, можно поступить следующим образом. Вначале определите различные атомы, входящие в формулу. Пусть количество этих атомов равно n, тогда существует 2n различных интерпретаций.
27. Опр. Аксиоматическая теория наз-сякатегоричной, если любые две ее модели изоморфны. Когда первоначальные понятия и аксиомы дают исчерпывающую совокупность главных принципов конкретной содержательной теории, тогда другие модели теории могут существовать, но они должны быть неотличимы (с точностью до терминологий и обозначений). Это явление и есть изоморфизм. Всякая полная и непротиворечивая аксиоматическая теорема категорична, но не всякая категоричная аксиоматическая теория полна. Т.К.Гёделя о полноте. Если формула F теории первого порядка T истинна в любой модели A этой теории, то F теорема теории T. Доказательство. Ввиду теоремы полноты нам нужно показать лишь, что формула есть теорема теории T тогда и только тогда, когда эта формула есть теорема в некоторой конечно аксиоматизируемой части теорииT. Это очевидно, так как в любом доказательстве может использоватьсялишь конечное число нелогических аксиом. Следствие. Теория T имеет модель тогда и только тогда, когда каждая конечно аксиоматизируемая часть теории T имеет модель. //Структура A для языка L теории T называется моделью теории T, если при каждой интерпретации все нелогические аксиомы из T принимают значение И. Другими словами структура A для языка L теории T —модель теории T, если все нелогические аксиомы из T истинны в структуре A. В определении речь идет лишь о нелогических аксиомах, т.к. логиче- ские аксиомы истинны в любой структуре.//
29. Языки специально созданы логикой в качестве средства точного анализа некоторых процедур мышления и, главным образом, логических выводов одних высказываний из других и доказательств высказываний. Особенности: 1. ЯЛП (язык логики предикатов) является искусственным языком; он предназначен для определенных целей (#, для аксиоматического построения теорий) 2. Если в обычных (естественных) языках выделяются синтаксический, семантический и прагматический аспекты,то в языках, которые подлежат описанию, имеются только синтаксический и семантический аспекты. 3. В искусственных языках логики имеется только объектная часть, точнее говоря, они содержат лишь средства для описания какой-то внешней по отношению к нему действительности. 4. ЯЛП характеризуют обычно как символический язык, потому что здесь используется особая символика, прежде всего для обозначения логических связей и операций. 5. ЯЛП обладает экстенсиональным характером. Он состоит в том, что предметные значения его термов (аналогов имен естественного языка) зависят лишь от предметных значений их составляющих, а истинные значения сложных формул от истинностных значений составляющих последних. Существуют различные способы формализации логики и соответственно различные формы (или типы) логических исчислений. Внутри каждого типа возможны также различные, но эквивалентные между собой (представляющие формализацию одной и той же содержательной логической теории) системы, различающиеся составом постулатов (аксиом и исходных правил вывода — в аксиоматических системах; исходных правил вывода — в натуральных системах; исходных секвенций и правил вывода для секвенций — в исчислениях секвенций). Построенное логическое исчисление может быть использовано как логический аппарат для осуществления выводов и доказательств в тех или иных нелогических теориях, построенных на базе соответствующего прикладного формализованного языка. Построение теории при этом осуществляется просто добавлением специальных ее аксиом к постулатам логического исчисления. В нелогических аксиомах (специальных) отражают свойства объектов, рассматриваемых в теории (#, свойства сложения, умножения и отношения
30. Теорема о неполноте и доказательство, утверждает примерно следующее: при определенных условиях в любом языке существуют истинные, но недоказуемые утверждения. Первая теорема Гёделя о неполноте Во всякой достаточно богатой непротиворечивой теории первого порядка (в частности, во всякой непротиворечивой теории, включающей формальную арифметику), существует такая замкнутая формула F, что ни F, ни Иначе говоря, в любой достаточно сложной непротиворечивой теории существует утверждение, которое средствами самой теории невозможно ни доказать, ни опровергнуть. Например, такое утверждение можно добавить к системе аксиом, оставив её непротиворечивой. Вторая теорема Гёделя о неполноте Во всякой достаточно богатой непротиворечивой теории первого порядка (в частности, во всякой непротиворечивой теории, включающей формальную арифметику), формула F, утверждающая непротиворечивость этой теории, не является выводимой в ней. Иными словами, непротиворечивость достаточно богатой теории не может быть доказана средствами этой теории. Однако вполне может оказаться, что непротиворечивость одной конкретной теории может быть установлена средствами другой, более мощной формальной теории. Но тогда встаёт вопрос о непротиворечивости этой второй теории, и т. д.
2. |
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 505. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 Конъюнкцией (логическим умножением –
Конъюнкцией (логическим умножением –  ) двух высказываний х и у называется новое высказывание…
) двух высказываний х и у называется новое высказывание… )двух высказываний …
)двух высказываний … истинна тогда, когда только один из ее членов является истинным, а другой – ложным.
истинна тогда, когда только один из ее членов является истинным, а другой – ложным.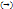 …
… двух высказываний…
двух высказываний… ) –отрицание дизъюнкции (ни A, ни B).
) –отрицание дизъюнкции (ни A, ни B).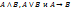 — формулы.
— формулы. В).Принзак равносильности формул: две формулы F и H алгебры высказываний равносильны тогда и только тогда, когда формула F1H является тавтологией
В).Принзак равносильности формул: две формулы F и H алгебры высказываний равносильны тогда и только тогда, когда формула F1H является тавтологией






 x
x 





 :
: 


 относительно
относительно 
 распределительный закон в арифметике
распределительный закон в арифметике





 «выводится», «доказывает»//
«выводится», «доказывает»// ,
, )
)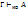 будем называть секвенцией, формулы из множества Г – гипотезами (посылками), а ф-лу А – следствием данной секвенции. Индекс ИВ можно опустить. Допустимы секвенции вида
будем называть секвенцией, формулы из множества Г – гипотезами (посылками), а ф-лу А – следствием данной секвенции. Индекс ИВ можно опустить. Допустимы секвенции вида 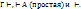 Читать:
Читать:  – формула А выводима в ИВ;
– формула А выводима в ИВ;  – система формул Г противоречива.//
– система формул Г противоречива.//
 – любая формула.
– любая формула.
 – аксиома L1 ИВ, утверждение посылки//
– аксиома L1 ИВ, утверждение посылки//

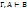 , длина вывода которых не больше n.
, длина вывода которых не больше n. при i≤n имеет некоторый вывод С1i, C2i,..., Cmi.
при i≤n имеет некоторый вывод С1i, C2i,..., Cmi. по индуктивному предположению уже имеются выводы. Можно считать, что Bj
по индуктивному предположению уже имеются выводы. Можно считать, что Bj  Тогда имеем вывод:
Тогда имеем вывод:
 :
:  //
// также будут формулами;
также будут формулами; также будут формулами;
также будут формулами;

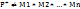
 .
. 2 тождественно истинных/ложных предиката равносильны, если заданы на одних и тех же множествах.
2 тождественно истинных/ложных предиката равносильны, если заданы на одних и тех же множествах. тождественно истинный n-местный предикат является следствиемдругого n-местного предиката, заданного на том же множестве.
тождественно истинный n-местный предикат является следствиемдругого n-местного предиката, заданного на том же множестве. где Q1..Qn –кванторы общности и существования,
где Q1..Qn –кванторы общности и существования, 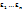 – переменные, φ – бескванторная формула.
– переменные, φ – бескванторная формула. )
) ), которую можно свести к формуле только с одно- и двух-местными предикатными переменными и т.д.
), которую можно свести к формуле только с одно- и двух-местными предикатными переменными и т.д. -формул и
-формул и  -формул.В этих случаях формула сводится к тождественной истинности формул на конечных множ-вах. Эти формул в предваренной нормальной форме содержат только соответствующие кванторы.
-формул.В этих случаях формула сводится к тождественной истинности формул на конечных множ-вах. Эти формул в предваренной нормальной форме содержат только соответствующие кванторы. общезначима тогда и только тогда, когда тождественно истинна на n-элементном множестве.
общезначима тогда и только тогда, когда тождественно истинна на n-элементном множестве. общезначима тогда и только тогда, когда тождественно истинна на одноэлементном множестве.
общезначима тогда и только тогда, когда тождественно истинна на одноэлементном множестве. .
.

 и n-арные предикатные символы
и n-арные предикатные символы  где n≥0;
где n≥0;
 и знак =.
и знак =.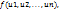 подразумевая вместо нее запись
подразумевая вместо нее запись  Отдельный нульарный функциональный символ - это терм (выражение
Отдельный нульарный функциональный символ - это терм (выражение  при n = 0 имеет вид f).
при n = 0 имеет вид f). , где
, где – термы.
– термы.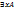 - формула.
- формула. )
) Это обусловлено следующей равносильностью:
Это обусловлено следующей равносильностью:  .
. для натуральных чисел)
для натуральных чисел) для их описания ведем понятия
для их описания ведем понятия является термом
является термом является формулой.
является формулой. ;
;

 ;
;

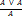



 из гипотез Г С1,…,Сi,…,Сm(1!), где Сm есть
из гипотез Г С1,…,Сi,…,Сm(1!), где Сm есть  (2!).
(2!). имеет вид
имеет вид 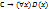 и получена из Bi
и получена из Bi  по правилу ввода
по правилу ввода  , где х е входит свободно в В). Доказательство остального не отличается от док-вав ИВ.
, где х е входит свободно в В). Доказательство остального не отличается от док-вав ИВ. (1i!), причем выполняется условие
(1i!), причем выполняется условие  (2i!).
(2i!). . Переменная х не входит свободно в
. Переменная х не входит свободно в 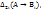 А и С, иначе в выводе (1!) при переходе от Bi к Bn она становилась бы связанной.
А и С, иначе в выводе (1!) при переходе от Bi к Bn она становилась бы связанной. :
: и
и
 . Тогда можем построить вывод секвенций
. Тогда можем построить вывод секвенций  :(D1,…,Dp=B) (3!) с
:(D1,…,Dp=B) (3!) с  .
.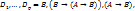 где
где  .
. выводима в ИПФ тогда и только тогда, когда предложение А выполняется на всякой алгебраической системе, на которой выполняютя все предложения из Г.
выводима в ИПФ тогда и только тогда, когда предложение А выполняется на всякой алгебраической системе, на которой выполняютя все предложения из Г. где A и B — формулы.
где A и B — формулы. не являются выводимыми в этой теории.
не являются выводимыми в этой теории.