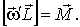Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Для того чтобы произвольная ось вращения тела сохраняла свое направление неизменным, к ней необходимо приложить определенные силы.
Момент импульса Суммарный момент импульса При вращении стержня вектор За промежуток времени dt вектор или в векторном виде
Поделив обе части последнего выражения на dt, получим
Таким образом, действительно, для удержания оси вращения в неизменном направлении к ней необходимо в данном случае приложить момент Движение твердого тела с одной неподвижной точкой. В качестве практически важного примера вращения твердого тела рассмотрим гироскоп. Гироскопом называют массивное симметричное тело, вращающееся с большой угловой скоростью вокруг своей оси симметрии.
Если ось вращающегося волчка наклонена к вертикали, то волчок не падает, а совершает так называемое прецессионное движение (прецессию) - его ось описывает конус вокруг вертикали с некоторой угловой скоростью Такое поведение волчка гироскопа можно легко объяснить с помощью уравнения моментов, если только принять, что
Поскольку ось волчка совпадает с одной из главных осей инерции, то, согласно (7.5),  При
Зная же поведение вектора Поведением вектора
В данном случае это момент силы тяжести Найдем связь между векторами
или в векторном виде
После подстановки этого выражения в (7.7) получим
Из этого уравнения видно, что момент силы Поэтому мгновенное устранение момента Заметим, что момент сил |
||||||||||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 253. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
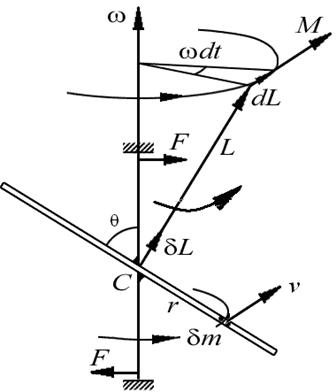
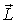 проще всего определить относительно точки С.
проще всего определить относительно точки С. 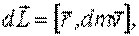 где
где 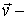 скорость элемента.
скорость элемента.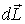 и не совпадает с вектором
и не совпадает с вектором 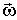 .
.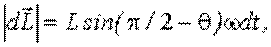
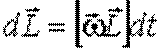 .
. (7.6)
(7.6)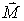 некоторых внешних сил
некоторых внешних сил 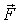 , показанных на рис. 7.7.
, показанных на рис. 7.7.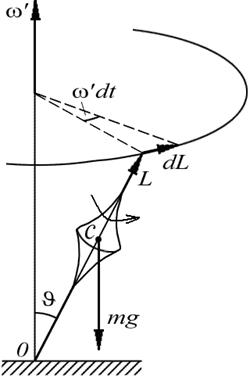
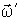 , причем, чем больше угловая скорость
, причем, чем больше угловая скорость 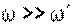 .
.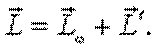
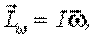 где
где 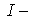 момент инерции волчка относительно этой оси.
момент инерции волчка относительно этой оси.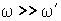 во всех практически интересных случаях
во всех практически интересных случаях 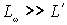 , поэтому результирующий момент импульса
, поэтому результирующий момент импульса 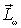 как по величине, так и по направлению, - можно считать, что
как по величине, так и по направлению, - можно считать, что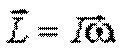
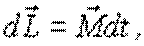
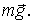 Из рис.7.8 видно, что
Из рис.7.8 видно, что  . В результате вектор
. В результате вектор 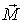 вокруг вертикали, описывая круговой конус с углом полураствора
вокруг вертикали, описывая круговой конус с углом полураствора 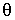 . Волчок-гироскоп будет прецессировать вокруг вертикальной оси с некоторой угловой скоростью.
. Волчок-гироскоп будет прецессировать вокруг вертикальной оси с некоторой угловой скоростью.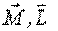 и
и 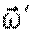 .
.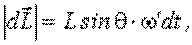 ,
,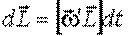 .
.