
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Вращение твердого тела вокруг свободных осей.Стр 1 из 3Следующая ⇒ Динамика твердого тела Уравнения движения и равновесия твердого тела. Вращение твердого тела вокруг неподвижной оси. Плоское движение твердого тела. Момент инерции. Примеры вычисления моментов инерции тел правильной формы. Динамика твердого тела
Вращение вокруг неподвижной оси.
С учетом выражения (5.9) лекции 6 запишем
где
где I- так называемый момент инерции твердого тела относительно оси 00':
Примеры поиска моментов инерции Момент инерции диска (цилиндра) относительно оси симметрии (проходящей через точку 0 перпендикулярно плоскости рисунка).
Первый способ Пусть масса однородного диска т, а его радиус и толщина равны R и h, соответственно. Тогда момент инерции элемента dm равен:
где r - плотность диска, r -расстояние до оси вращения, а элемент объема dV взят в цилиндрической системе координат. Интегрируя по углам j и радиусу r, получаем момент инерции диска (цилиндра):
Второй способ
Рассмотрим бесконечно тонкое кольцо с внутренним радиусом r наружным радиусом r + dr. Площадь такого кольца Его момент инерции равен Момент инерции всего диска определяется интегралом Элемент массы представим в виде  тогда
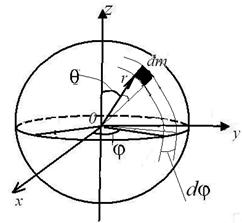
Момент инерции однородного шара массы т и радиуса R относительно оси проходящей через центр. Первый способ
Шар удобнее рассматривать в сферической системе координат, тогда момент инерции элемента dm равен:
Интегрируя по всем переменным:
и учитывая, что масса шара равна получаем момент инерции шара относительно оси симметрии:
Второй способ
где
Момент инерции сферического слоя относительно диаметра равен
Интегрируя, получаем момент инерции сплошного шара
Теорема Штейнера:
Доказательство этой теоремы - рассмотреть самостоятельно. Момент инерции относительно точки
Hi
Свободные оси. Главные моменты инерции. Ось вращения, направление которой в пространстве остается неизменным без действия на нее каких-либо сил извне, называют свободной осью тела. В общей теории доказывается, что для любого твердого тела существуют три взаимно перпендикулярные проходящие через центр инерции тела оси, которые могут служить свободными осями. Их называют главными осями инерции тела.
Для вращения вокруг главных осей инерции (х, y, z) можно записать
Однако, если вращение происходит вокруг произвольных осей (x,y, z), то связь между компонентами становится более сложной:
или:
Тензор инерции характеризует инертные свойства тела при вращении.
Найдем выражение для тензора инерции. Запишем момент импульса для элемента массы:
где вектор ri откладывается от центра масс. Двойное векторное произведение раскладываем по известному правилу векторной алгебры (легко проверить, расписывая векторные произведения):
Тогда
Найдем проекцию на ось х
Откуда, рассматривая аналогично другие проекции, получаем тензор момента инерции в виде: .
Тензор симметричный. Тензор и его компоненты вычисляются с помощью интегрирования, так, например:
Если в качестве координатных осей взять главные оси инерции, то тензор становится диагональным:
Важной особенностью главных осей инерции тела является то, что при вращении тела вокруг любой из них момент импульса
где I - момент инерции тела относительно данной главной оси инерции. Причем Вращение твердого тела вокруг свободных осей. |
||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 288. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |



 и
и  - масса и расстояние от оси вращения
- масса и расстояние от оси вращения  частицы твердого тела,
частицы твердого тела,  - его угловая скорость. Обозначив величину, стоящую в круглых скобках, через I, получим
- его угловая скорость. Обозначив величину, стоящую в круглых скобках, через I, получим





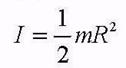

 .
.

 ,
,


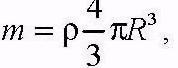
 .
. ,
, —объем сферического слоя,
—объем сферического слоя,  — объем всего шара.
— объем всего шара.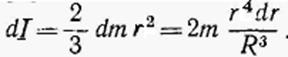


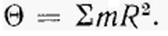


 ,
,  ;,
;, 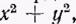


 , где R — расстояние точки т от начала координат О. Поэтому
, где R — расстояние точки т от начала координат О. Поэтому
 a)
a)  б)
б)  в)
в)  г)
г)



 - тензор инерции.
- тензор инерции.
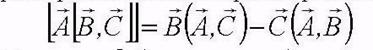
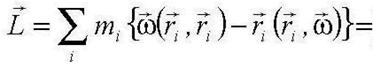



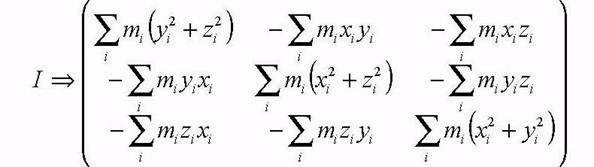


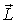 тела совпадает по направлению с угловой скоростью
тела совпадает по направлению с угловой скоростью  тела и определяется формулой
тела и определяется формулой