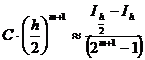Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Глава III. Численное интегрирование§ 1. Простейшие квадратурные формулы. Составные формулы
Задача: вычислить Опр. Квадратурная формула — x0, x1, ..., xn и весами q0, ..., qn . Квадратурная формула называется точной для многочленов степени m, если для любого многочлена, степени ≤ m, подставленной вместо f(x), формула дает точное равенство.
I. Формула прямоугольников.
Формула точна для многочленов степени 1.
II. Формула трапеций. Формула также точна для многочленов степени 1.
III. Формула Симпсона. Пусть
Формула также точна для многочленов степени 2 (без док-ва).
Составные формулы получаются, если [a,b] разбить на N частей, на каждой части применить простую формулу, и результаты сложить. Пусть Составная формула прямоугольников:
Составная формула трапеций:
Пусть
Составная формула Симпсона:
§ 2. Метод неопределенных коэффициентов
Пусть известны узлы x0, ..., xn на [a,b]. Найдем квадратурную формулу 1=x0, x, x2,...,xm получится система уравнений:
Это СЛУ с неизвестными q0, ..., qn.
В этой СЛУ (m+1) уравнений, (n+1) неизвестных.
Если m = n, то главный определитель системы
— определитель Вандермонда (транспонированный). Следовательно, решение q0, ..., qn существует и единственно.
Пример. Пусть m =2, n =2, СЛУ:
Получили формулу Симпсона.
§ 3. Формулы Ньютона-Котеса
Пусть d0, ..., dn Î [–1;1] (вспомогательные узлы, сначала различные, потом возможно совпадающие) 
f(xi) , для i = 0,...,n. Пусть Ln(x) — интерполяционный многочлен Лагранжа по узлам xi. Тогда
Выполним замену:
Замечание: В случае, когда среди d0, ..., dn есть совпавшие (следовательно, среди x0, ..., xn тоже), вместо многочлена Лагранжа используют интерполяционный многочлен с кратными узлами. Однако результат так же записывают в виде Опр. Квадратурные формулы Ньютона-Котеса — формулы вида
Свойства: 1. Если p(x) четна (симметрична) относительно 2. "Симметричные" квадратурные формулы точны для любой функции, нечетной относительно Частные случаи: при p(x) º 1 1)n = 0; d0 = 0 — формула прямоугольников. 2)n = 1; d0 = –1, d1 = 1 — формула трапеций. 3)n = 2; d0 = –1, d1 = 0, d2 = 1 — формула Симпсона.
4)n = 1; d0 = 0 = d1 — формула прямоугольников. 5)n = 3; d0 = –1, d1 = 0, d2 = 1, d3 = 0 — формула Симпсона.
§ 4. Формулы Гаусса
Задача: Дано: n — количество узлов; [a,b] — отрезок; p(x) > 0 на [a,b]. Найти: квадратурную формулу Опр. Квадратурная формула Гаусса — решение поставленной задачи. Теорема. Существует решение для m = 2n – 1. Доказательство: 1) При подстановке в квадратурную формулу простых многочленов 1=x0, x, x2,...,xm получится система уравнений:
В этой системе (m+1) нелинейное уравнение с 2×n неизвестными x0, ..., xn–1 , D0, ...,Dn-1. При (m+1) = 2×n решений конечное число (если оно существует). Следовательно, m = 2×n – 1. 2) Существование решения будет показано ниже.
Опр. Скалярным произведением функций f(x) и g(x) (с комплексными значениями) называется
Опр. Многочлен g(x) ортогонален многочлену g(x), соответственно p(x) и [a,b], если (f(x),g(x)) = 0.
Обозначим
Пример. 1. Многочлены Чебышева 2. Многочлены Лежандра:
Если многочлен Пусть эти корни x0, ..., xn–1 — узлы интерполяции. Найдем по ним квадратурную формулу Лемма. Если x0, ..., xn–1 — корни (нули) многочлена Доказательство: Пусть Q2n–1(x) — произвольный многочлен степени (2n–1). По теореме о делении многочленов с остатком выполняется Найдем
Примеры: при p(x) º 1, на [–1;1] 1)n = 1; x0 = 0; D0 = 2, т.е. формула
2)n = 2; x0 = – 0,577; x1 = 0,577; D0 = D1 = 1, т.е. формула
3)n = 3; x0 = – 0,775; x1 = 0; x2 = 0,775; D0 = 0,556; D1 = 0,889; D2 = 0,556, т.е. формула
Замечание: Чтобы использовать эти узлы и коэффициенты для интеграла на произвольном отрезке [a,b], нужно в интеграле выполнить замену переменной Тогда
Составная формула Гаусса, для p(x) º 1: отрезок [a,b] разбивается на N частей одинаковой длины, каждая часть тоже разбивается на n – 1 частей, точки деления — xki , где k = 0,...,N – 1, i= 0,...,n – 1. Тогда
§ 5. Погрешность квадратурных формул. Правило Рунге.
Пусть квадратурная формула
Тогда
Т.е. Пример. 1) Для простейших формул прямоугольников и трапеций
2) Для формулы Симпсона
Теперь воспользуемся разложением f(x) по формуле Тейлора степени (m+1):
Тогда
Опр. Главным членом погрешности называется Правило Рунге — способ оценки главного члена погрешности без использования производной (m + 1) порядка.
Пусть Ih — приближенное значение интеграла Тогда
|
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 196. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 для f(x), непрерывной на [a,b].
для f(x), непрерывной на [a,b]. , определяемая узлами
, определяемая узлами .
.
 , где
, где  .
.
 .
.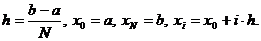
 .
.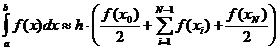


 .
. , для j = 0,...,m.
, для j = 0,...,m. , для j = 0,...,m.
, для j = 0,...,m.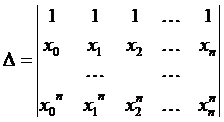

 Û
Û  Û
Û 
 , для i = 0,...,n.
, для i = 0,...,n. , где p(x) — некоторая фиксированная функция, называемая весовой функцией.
, где p(x) — некоторая фиксированная функция, называемая весовой функцией.




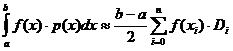 .
. .
. , т.е.
, т.е.  и xi расположены симметрично вокруг
и xi расположены симметрично вокруг  .
. , точную для многочленов наибольшей степени m, (т.е. найти узлы x0, ..., xn–1 и коэффициенты D0, ...,Dn-1).
, точную для многочленов наибольшей степени m, (т.е. найти узлы x0, ..., xn–1 и коэффициенты D0, ...,Dn-1). , для j = 0,...,m.
, для j = 0,...,m. , где
, где 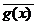 – комплексно сопряженная к g(x).
– комплексно сопряженная к g(x). многочлен степени n, со старшим коэффициентом =1, ортогональный всем многочленам меньшей степени.
многочлен степени n, со старшим коэффициентом =1, ортогональный всем многочленам меньшей степени. — соответствуют
— соответствуют 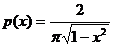 и [–1;1].
и [–1;1]. — соответствуют p(x) º 1 и [–1;1].
— соответствуют p(x) º 1 и [–1;1]. .
. .
.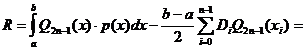


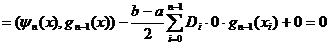 . Лемма доказана.
. Лемма доказана. точна для многочленов степени 2×1–1 = 1.
точна для многочленов степени 2×1–1 = 1. точна для многочленов степени 2×2–1 = 3.
точна для многочленов степени 2×2–1 = 3. точна для многочленов степени 2×3–1 = 5.
точна для многочленов степени 2×3–1 = 5. .
. . Т.е. коэффициенты D0, ...,Dn-1 не изменятся, а узлы пропорционально преобразуются в узлы на отрезке [a,b].
. Т.е. коэффициенты D0, ...,Dn-1 не изменятся, а узлы пропорционально преобразуются в узлы на отрезке [a,b]. .
.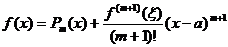 .
.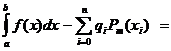

 .
. — погрешность квадратурной формулы.
— погрешность квадратурной формулы. .
. .
.
 /
/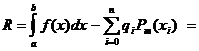
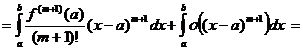

 .
. .
. .
. .
. .
.