
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Глава II. Аппроксимация и интерполяцияСтр 1 из 3Следующая ⇒ § 1. Основные понятия
Задача: Дано: x0, x1, ..., xn — узлы, f(x0), f(x1), ..., f(xn) — значения f(x) в узлах. Найти: функцию g(x), такую, что g(xi) = f(xi), i=0,...,n. Если в дальнейшем нужно вычислить значение g(x) для Если
Примером решения задачи является использование многочлена Тейлора m-ой степени:
Для x0=0 можно использовать известные разложения для функций:
Погрешность метода — остаточный член формулы Тейлора в форме Лагранжа:
Кроме того, если § 2. Существование и единственность интерполяционного многочлена
Задача: Дано: x0, x1, ..., xn — узлы, f0, f1, ..., fn — значения f(x) в узлах. Найти: Lm(xi) = fi, i=0,...,n. Теорема. Существует единственный многочлен степени Док-во: Чтобы найти многочлен Lm(x) нужно найти коэффициенты a0,a1,...an. Они должны удовлетворять СЛУ В системе (m+1) неизвестных, (n+1) уравнение. Если система крамеровская, то решение существует и единственное.
Пусть m+1= n+1, т.е. m=n. Главный определитель системы
Замечание (иллюстрация): Если m<n, СЛУ может быть несовместна. Например, m=1, n=2, найти линейную функцию (прямую), проходящую через три точки:
Например, m=2, n=1, найти квадратичную функцию (параболу), проходящую через две точки: 
§ 3. Интерполяционный многочлен Лагранжа
Выразим многочлен Ln(x) как линейную комбинацию значений f0, f1, ..., fn:
Рассмотрим в качестве подсказки частные случаи. 1) n=1 x0, x1 — узлы f0, f1 — значения Найти
при x0 при x1
2) n=2 x0, x1, x2— узлы f0, f1, f2 — значения Найти
при x0 при x1 при x2
Опр. Интерполяционным многочленом Лагранжа называется
Опр. Лагранжевы коэффициенты —
Замечание: Лагранжевы коэффициенты удовлетворяют тождеству
§ 4. Погрешность интерполяционного многочлена Лагранжа
Пусть f(x) — непрерывная, имеющая непрерывные производные до (n+1) порядка. Ln(x) — многочлен Лагранжа: Ln(xi)=f(xi) для всех i=0,...,n. [a,b] — отрезок, содержащий узлы x0, x1, ..., xn.
Найдем оценку отличия значения f(x) от значения Ln(x) в точке
Запишем равенство
Рассмотрим функцию
Т.е. существует Т.к.
Þ
§ 5. Минимизация погрешности интерполяционного многочлена Лагранжа. Многочлен Чебышева
Задача: Дано: f(x) на [a,b], непрерывная и дифференцируемая до (n+1) порядка. Найти: x0, x1, ..., xn — узлы, такие, что максимальная погрешность
Ослабление задачи: Случай 1) Пусть [a,b]=[-1,1]. Опр. Многочленом Чебышева на [-1,1] называется
Выведем рекуррентную формулу для многочленов Чебышева. Сначала отметим Обозначим +
Þ
Þ
Þ
Свойства многочленов Чебышева: 1) Если n – четно (нечетно), то Tn(x) содержит только четные (нечетные) степени x. Док-во: по индукции. 2) Старший коэффициент Tn(x) равен 2n–1 (для n ³ 1). Док-во: по индукции. 3) Многочлен Tn(x) имеет n действительных корней в интервале (–1,1), по формуле
Док-во: подстановкой. 4) Док-во: по определению. 5) Многочлен 21-n×Tn(x) имеет старший коэффициент 1 (для n ³ 1) и выполняется неравенство
(Без док-ва)
Замечание: Многочлен Чебышева — "многочлен, наименее уклоняющийся от нуля".
Теорема 1 (без док-ва). Корни многочлена Tn+1(x), т.е.
Случай 2) Произвольный [a,b]. Введем новую переменную Тогда f(t) определена на [–1,1]. Используя
Теорема 2 (без док-ва). Значения
§ 6. Схема Эйткена
Для упрощения вычисления интерполяционного многочлена Ln(x) используется следующая схема: Схема Эйткена Обозначим L(k,k+1,...,l)(x) — интерполяционный многочлен по узлам xk,xk+1,...xl. Заметим, что L(k)(x) = fk, L(0,1,...,n)(x) = Ln(x). Утверждение. Выполняется равенство
Док-во: Левая часть равенства — L(k,k+1,...,l)(x) — многочлен степени (l–(k–1)–1)=l–k по узлам xk,xk+1,...xl.. В правой части равенства — тоже многочлен такой же степени. Для любого i = k+1,...,l–1 значения левой и правой частей совпадают:
Для xk выполняется
Для xl выполняется
Вычисление выполняется при помощи таблицы следующего вида:
§ 7. Численное дифференцирование
Задача: Дано: x0, x1, ..., xn — узлы, f0, f1, ..., fn — значения f(x) в узлах. Найти:
1 способ) Поскольку f(x) » Ln(x), то 2 способ) Метод неопределенных коэффициентов. Пусть где ci — коэффициенты, обеспечивающие точность формулы для функций f(x), являющихся многочленами наиболее высокой степени. Если произвольный многочлен a0+a1x+...+anxn степени n взят в качестве f(x), то выполняется
Равенство возможно только если коэффициенты при aj совпадают, т.е.
Получаем СЛУ с неизвестными c0,...cn, (n+1) неизвестных, (n+1) уравнений. (Такая же система получается, если в формулу (1) подставлять простые многочлены степени £ n, т.е. 1=x0, x, x2,...,xn). Главный определитель системы
— определитель Вандермонда (транспонированный). Следовательно, решение c0,...cn существует и единственно.
3 способ) Использование простейших формул численного дифференцирования.
Вывод первой формулы: пусть даны x0, x1 — узлы, f0, f1 — значения f(x) в узлах, h = x1 – x0 расстояние между узлами. По определению производной функции в точке Þ
Замечание: Очевидно, формула точна для многочленов степени 1.
Вывод второй формулы: пусть даны x0, x1, x2 — узлы, f0, f1 , f2 — значения f(x) в узлах, h = x1 – x0 = x2 – x0 расстояние между узлами. Найдем формулу для производной в средней точке: Упростим задачу: пусть -h,0,h – узлы, f0, f1 , f2 — значения. Подставим в нее 1=x0, x, x2. Получим СЛУ:
Решение системы Тогда По причине линейности для произвольных узлов x0, x1, x2 можно использовать те же коэффициенты, следовательно
Формула точна для многочленов степени 2.
Вывод третьей формулы: пусть даны x0, x1, x2 — узлы, f0, f1 , f2 — значения f(x) в узлах, h = x1 – x0 = x2 – x0 расстояние между узлами. Найдем формулу для второй производной в средней точке: Упростим задачу: пусть -h,0,h – узлы, f0, f1 , f2 — значения. Подставим в нее 1=x0, x, x2. Получим СЛУ:
Решение системы Тогда По причине линейности для произвольных узлов x0, x1, x2 можно использовать те же коэффициенты, следовательно
Формула также точна для многочленов степени 2. Д/З Вывести формулы для вычисления
§ 8. Погрешность простейших формул численного дифференцирования
Первая формула или Для оценки погрешности воспользуемся разложением по формуле Тейлора:
Þ
Þ
Вторая формула или Для оценки погрешности также воспользуемся разложением по формуле Тейлора:
Вычтем из первой строки вторую и поделим на 2h:
Поскольку
Þ
Третья формула или Для оценки погрешности также воспользуемся разложением по формуле Тейлора:
Сложим строки и поделим на h2:
Существует точка
Þ формулы (4). Замечание: говорят, что первая погрешность имеет порядок h, а вторая и третья — порядок h2. § 9. Разделенные разности. Многочлен Ньютона.
Вступление: схема Эйткена, формулы вычисления производных, используют разности значений функций, деленные на расстояния между узлами. Похожие формулы называют разностными методами.
Опр. Назовем разделенными разностями 0-го порядка значения f(xi). Назовем разделенными разностями 1-го порядка:
Назовем разделенными разностями 2-го порядка:
Назовем разделенными разностями порядка l:
Для вычисления всех разделенных разностей используют таблицу, как в схеме Эйткена:
Лемма 1.(без док-ва)
Опр. Интерполяционным многочленом Ньютона с разделенными разностями называется
Теорема 2. Многочлен Ньютона совпадает с многочленом Лагранжа.
Док-во: 1) где Lk(x) — многочлен Лагранжа степени k по узлам x0,...,xk. 2) 3) Покажем, что для любого k выполняется По определению многочлена Лагранжа
Замечание: если x0 < x1 < … < xn , то
— интерполяционный многочлен для интерполяции вперед;
— интерполяционный многочлен для интерполяции назад. § 10. Интерполяция с кратными узлами
Задача: Дано: x0, x1, ..., xn — узлы (различные), m0,..., mn — кратности (натуральные числа), s = m0 +...+ mn Найти: многочлен g(x) степени (s–1), такой, что:
– – – – – – – – – –
Утверждение. Многочлен g(x) определяется единственным образом.
Док-во: Существование такого многочлена будет показано ниже, в описании алгоритма его нахождения. Докажем единственность методом "от противного". Предположим, существуют два многочлена степени (s–1), удовлетворяющих условиям задачи. Обозначим их разность Q(x). Тогда Q(x) — многочлен степени (s–1) (или ниже), удовлетворяющий условиям:
– – – – – – – – – –
Следовательно, у многочлена Q(x) число x0 – корень кратности m0 , и т.д. Таким образом, Q(x) имеет s корней с учетом их кратностей. Но многочлен степени (s–1) не может иметь более (s–1) корней, следовательно Q(x)º0. Утв. доказано.
Для нахождения g(x) сведем задачу к задаче поиска интерполяционного многочлена с s узлами. Пусть e > 0 — некоторая переменная величина, введем узлы При e®0 При достаточно маленьком e все
По таблице разделенных разностей:
Найдем многочлен Ньютона
Запишем в более коротком виде:
Тогда его предел при e®0 имеет вид:
Заметим, что В противном случае, Алгоритм нахождения g(x): 1) Записать массив предельных значений узлов x0,...,x0,x1, ...,x1,...,xn,..., xn (каждый узел повторяется столько раз, какова его кратность). 2) Составить таблицу предельных значений разделенных разностей:
3) Составить многочлен Ньютона, используя верхнюю строку таблицы и массив узлов с повторами.
Пример. Дано: 0,1 — узлы; 2,3 — кратности; f(0)=0, f '(0)=1, f(1)=2, f '(1)=0, f "(1)=2. Найти многочлен степени 4, удовлетворяющий перечисленным условиям. 1) Массив узлов с повторами: (0,0,1,1,1). 2)
3) g(x) = 0+1(x–0)+1(x–0)2–3x2(x–1)+6x2(x–1)2 = 6x4–15x3+10x2+x.
§ 11. Кубическая сплайн-интерполяция
Пусть [a,b] разбит на N равных частей. Точки деления a = x0, x1, ..., xn = b. Длина каждого участка Опр. Сплайн — функция, непрерывная вместе с производными до некоторого порядка на [a,b], являющаяся многочленом на каждом [xi–1,xi] ("кусочная функция").
Степень сплайна — максимальная из степеней многочленов.
Дефект сплайна — разность между степенью сплайна и наивысшим порядком непрерывной производной.
Сплайн-интерполяция — замена функции f(x) на сплайн, имеющий в узлах те же значения, что и f(x), и те же значения производных.
Опр. Кубический сплайн — сплайн третьей степени, имеющий непрерывную производную первого порядка. Обозначение: S3(x). Опр. Наклон сплайна в точке xi — значение производной Рассмотрим один отрезок [xi–1,xi], h = xi – xi–1. Пусть fi–1, fi — значения функции (следовательно, сплайна тоже), fsi–1,fsi — значения производной функции. Как в задаче интерполяции с кратными узлами, кратность каждого узла равна 2. Тогда существует многочлен степени 2+2–1 = 3, удовлетворяющий условиям задачи. Составим таблицу предельных значений разделенных разностей:
После преобразования, найденную функцию можно записать в виде линейной комбинации значений fi–1, fi и fsi–1,fsi:
Применение кубической сплайн-интерполяции: При большом количестве N узлов интерполяции, когда поиск интерполяционного многочлена большой степени требует большого объема вычислений, вместо него находят кубический сплайн, составленный из многочленов третьей степени, определенных каждый на своем отрезке между узлами.
Если не известны наклоны сплайна (т.е. значения производной в узлах), вычисляют их примерное значение по формулам численного дифференцирования:
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 191. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 , то говорят об интерполяции функции.
, то говорят об интерполяции функции. (т.е. лежит за пределами отрезка, содержащего узлы), то говорят об экстраполяции.
(т.е. лежит за пределами отрезка, содержащего узлы), то говорят об экстраполяции. .
. .
.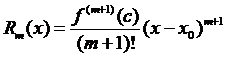 , где c лежит между x и x0.
, где c лежит между x и x0. не принадлежит интервалу сходимости ряда Тейлора, то погрешность не уменьшается.
не принадлежит интервалу сходимости ряда Тейлора, то погрешность не уменьшается. , такой, что
, такой, что , удовлетворяющий условиям задачи.
, удовлетворяющий условиям задачи. , i=0,...,n.
, i=0,...,n. — определитель Вандермонда.
— определитель Вандермонда. . Если все узлы различны, то
. Если все узлы различны, то  . Теорема доказана.
. Теорема доказана.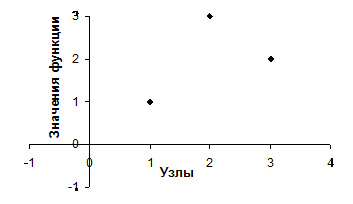
 Если m>n, СЛУ имеет бесконечно много решений.
Если m>n, СЛУ имеет бесконечно много решений. .
.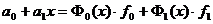











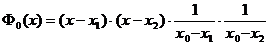
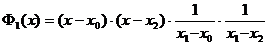

 .
. для каждого i = 0,...,n.
для каждого i = 0,...,n. .
. , не совпадающей ни с одним из узлов.
, не совпадающей ни с одним из узлов. , где
, где  .
. .
.



 :
:  .
. , и
, и  , получаем
, получаем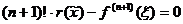 , следовательно
, следовательно  .
. .
. .
. .
. была бы минимальной.
была бы минимальной. ® min.
® min. .
. ,
,  .
. Þ
Þ




 , i = 0,...,n–1.
, i = 0,...,n–1. , причем
, причем  , m = 0,...,n.
, m = 0,...,n. для любого многочлена Pn(x) степени n со старшим коэффициентом 1.
для любого многочлена Pn(x) степени n со старшим коэффициентом 1. , i = 0,...,n, минимизируют
, i = 0,...,n, минимизируют  в оценке погрешности интерполяционного многочлена. При этом
в оценке погрешности интерполяционного многочлена. При этом и
и  .
.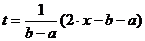 .
. , i = 0,...,n, находим
, i = 0,...,n, находим  .
.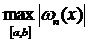 в оценке погрешности интерполяционного многочлена. При этом
в оценке погрешности интерполяционного многочлена. При этом и
и  .
. .
. .
. .
. . Утв. доказано.
. Утв. доказано.

 .
. (для 1 £ m £ n).
(для 1 £ m £ n).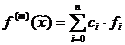 , (1)
, (1) для любых a0,a1,...an.
для любых a0,a1,...an. для i = 0,...,n.
для i = 0,...,n.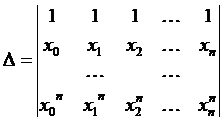
 .
. , т.е.
, т.е.  (2)
(2) , т.е. производная в x1 также вычисляется по формуле (2).
, т.е. производная в x1 также вычисляется по формуле (2).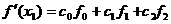 .
. — искомая формула.
— искомая формула. Û
Û  .
.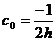 ,
,  ,
,  .
. .
. (3)
(3) .
. — искомая формула.
— искомая формула. Û
Û  .
. ,
,  ,
,  .
. .
. (4)
(4) через
через  и для
и для  через
через  методом неопределенных коэффициентов.
методом неопределенных коэффициентов. (2)
(2) .
. , где
, где  .
. .
. — погрешность формулы (2).
— погрешность формулы (2).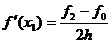 (3)
(3) .
. , где
, где 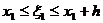 ,
, , где
, где  .
. .
. , существует точка
, существует точка  , такая что
, такая что  (предполагая непрерывность третьей производной).
(предполагая непрерывность третьей производной). — погрешность формулы (3).
— погрешность формулы (3).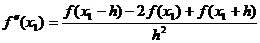 .
. , где
, где  , где
, где  .
. (предполагая непрерывность четвертой производной).
(предполагая непрерывность четвертой производной). — погрешность
— погрешность .
. .
. .
.
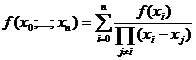 .
. .
.
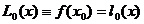 .
. .
.


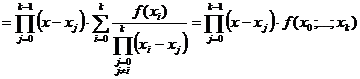 . Теорема доказана.
. Теорема доказана.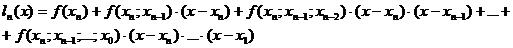
 ,
, .
. ,
, .
. , для i = 0,...,n; j = 1,...,mi.
, для i = 0,...,n; j = 1,...,mi. .
. различны.
различны.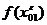






 , где
, где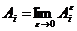 .
.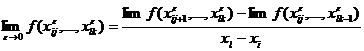 , т.е. обычная разделенная разность, если i ¹ l.
, т.е. обычная разделенная разность, если i ¹ l. (доказывается по индукции).
(доказывается по индукции).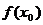



 .
. .
.





 , для i = 1,...,N–1
, для i = 1,...,N–1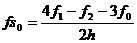 ,
,  .
.