
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Граничные условия для векторов Е и D. ⇐ ПредыдущаяСтр 2 из 2 В рассмотренном выше примере (см. Рис.3) было получено, что вектор электрической индукции им
Рис.4 Как видно из рисунка, поле вне диэлектрика направлено под некоторым углом к нормали проведенной к границе диэлектрика. В этом случае напишем изменение поля с учетом плотности поверхностных зарядов на границе диэлектрика по компонентам используя систему координат, показанную на рисунке: Из рисунка видно, что поле поверхностных зарядов меняет только проекцию на ось X. Согласно (11) поверхностная плотность зарядов и связи вектора поляризации (7) с напряженностью поля в диэлектрике (8) для Y-вой проекции поля в диэлектрике из (17b) получаем: Отсюда для поля в диэлектрике получаем: А для вектора электромагнитной индукции имеем (с учетом определения (14)):  Таким образом, уже на этом примере видно, что при переходе из одного диэлектрика (вакуум можно считать идеальным диэлектриком) в другой:
Всё это хорошо, но возникает вопрос насколько правомерно такое обобщение результатов нашей частной задачи на общий случай? Оказывается, что это правильное обобщение. Чтобы доказать это рассмотрим границу между двумя диэлектриками с диэлектрическими проницаемостями Откуда это равенство? О нем говорилось, когда обсуждалась работа консервативных сил, которая должна быть равна нулю по всякому замкнутому контуру. В свою очередь мы уже показали, что электрические силы консервативные. Напряженность поля и сила, действующая на заряд, отличаются на постоянный множитель равный величине заряда. Таким образом, уравнение (21) есть следствие консервативности электрических сил. В бесконечно малой окрестности любую поверхность с точностью до бесконечно малых второго порядка можно аппроксимировать касательной плоскостью. Такая плоская граница раздела показана на Рис.5.
Рис.5 Вычислим интеграл (21) по контуру ABCD. Считая контур бесконечно малым можно вычислить интеграл на каждом участке в среднем. В таком случае имеем: где Устремляя b к нулю, получим: Или, учитывая определение вектора электромагнитной индукции: Такой ответ мы уже получали в нашем примере. Единственное замечание — здесь ось X это любая ось, лежащая в плоскости, касательной к поверхности раздела. Такая составляющая (проекция на ось лежащую в касательной плоскости), называется тангенциальной и означается индексом Поскольку мы можем считать a как угодно малой величиной, то можно сказать, что непрерывность тангенциальных составляющих вектора напряженности электрического поля выполняется для каждой точки поверхности раздела (сравни с (19)). Для получения условий на нормальные составляющие векторов
Рис.6 Поток вектора электромагнитной индукции через поверхность этого цилиндра приближенно можно записать в виде:
Здесь введено обозначение Пользы от такого уравнения немного, поскольку поверхностные плотности зарядов мы не знаем. Конечно, можно потрудиться, использовать связь поверхностной плотности с вектором поляризации. И если проделать все эти выкладки, то от уравнения (27) придем к уравнению (26), с которым ещё немного поработаем. Устремим высоту цилиндра к нулю, оставляя пока радиус основания конечным. В таком случае интеграл по боковой поверхности стремится к нулю, и мы приходим к равенству: Из Рис.6 видно, что нормали Таким образом, доказано, что при переходе из одной среды в другую нормальная составляющая вектора электромагнитной индукции остается непрерывной, и как следствие нормальная составляющая вектора напряженности электрического поля испытывает скачок, который вычисляется из выражения (см. связь между Все эти соотношения мы раньше получали для частного случая плоской пластинки помещённой в вакуум. Заметим, что если поверхность раздела совпадает с эквипотенциальной поверхностью, то тангенциальная составляющая вектора |
|||||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 914. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
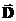 не меняется при переходе из вакуума в диэлектрик. Поле в диэлектрике находится из связи вектора напряженности
не меняется при переходе из вакуума в диэлектрик. Поле в диэлектрике находится из связи вектора напряженности 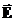 с вектором
с вектором 
 (17a)
(17a)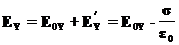 (17b)
(17b)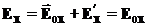 (17b)
(17b)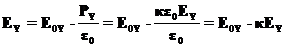 (18)
(18)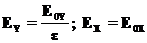 (19)
(19)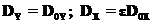 (20)
(20)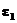 и
и 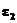 . Будем опираться на следующее уравнение для вектора напряженности электрического поля:
. Будем опираться на следующее уравнение для вектора напряженности электрического поля: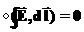 (21)
(21)
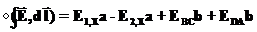 , (22)
, (22)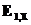 и
и 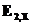 средние значения проекций поля на ось X в первом и втором диэлектриках на линиях AB и CD соответственно, а
средние значения проекций поля на ось X в первом и втором диэлектриках на линиях AB и CD соответственно, а 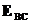 и
и 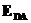 средние значения напряженности поля на отрезках BC и DA. Если учесть, что интеграл (22) всегда равен нулю, получим
средние значения напряженности поля на отрезках BC и DA. Если учесть, что интеграл (22) всегда равен нулю, получим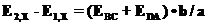 , (23)
, (23)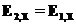 , (24a)
, (24a)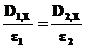 . (24b)
. (24b) . Поэтому обычно условия (24a) и (24b) записываются в виде, когда не надо пояснять, как выбрана ось Y:
. Поэтому обычно условия (24a) и (24b) записываются в виде, когда не надо пояснять, как выбрана ось Y: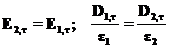 (25)
(25)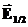 и
и 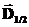 воспользуемся теоремой Гаусса для вектора электромагнитной индукции (16). Для этого рассмотрим круговой цилиндр высоты h с образующими параллельными нормали к поверхности раздела, и радиусом основания
воспользуемся теоремой Гаусса для вектора электромагнитной индукции (16). Для этого рассмотрим круговой цилиндр высоты h с образующими параллельными нормали к поверхности раздела, и радиусом основания 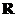 как это показано на Рис.6.
как это показано на Рис.6.
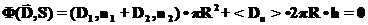 , (26)
, (26)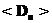 для средней проекции вектора
для средней проекции вектора 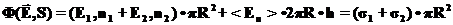 . (27)
. (27)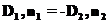 . (28)
. (28)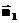 и
и 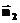 направлены в разные стороны. Это означает, что при проектировании на какую-нибудь одну из нормалей проекция вектора
направлены в разные стороны. Это означает, что при проектировании на какую-нибудь одну из нормалей проекция вектора 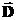 оказывается непрерывной:
оказывается непрерывной: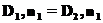 или
или 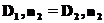 (29)
(29)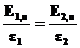 (30)
(30)