
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Электрическое поле в диэлектрике. Электрическое смещение.Стр 1 из 2Следующая ⇒ Электрическое поле в веществе. Диэлектрики. Поляризуемость и диэлектрическая проницаемость. Электрическое поле в диэлектрике. Электрическое смещение. Теорема Гаусса для векторов E и D. Граничные условия для векторов Е и D. Проводники в электрическом поле. Электрическая емкость проводника. Конденсаторы. Диэлектрики. Поляризуемость и диэлектрическая проницаемость. В предыдущем разделе рассматривалось электростатическое поле в вакууме. Распределение поля в веществе существенно зависит от свойств вещества. Поэтому раздельно будут рассмотрены два предельных случая вещества — диэлектрики и проводники. Диэлектрики, которые ещё называются изоляторами, практически не содержат свободных зарядов, тогда как в проводниках таких свободных зарядов много.
Прямо сейчас мы обсудим, как изменяется электрическое поле в диэлектриках, а о проводниках поговорим несколько позже. Для этого рассмотрим, как устроены диэлектрики в микроскопическом масштабе. Из курса химии известно, что мельчайшей частицей вещества является молекула. Обычные молекулы (мы будем иметь дело только с такими молекулами) имеют размер в несколько ангстрем (  ). В свою очередь молекулы состоят из атомов. Для наших целей достаточно считать, что атом состоит из положительно заряженного ядра и электронов, суммарный заряд которых отрицательный и в точности равен заряду ядра. Таким образом, атом, и как следствие молекула, (объект, состоящий из нескольких атомов) являются электрически нейтральными объектами. Мы будем рассматривать электрические поля не насколько сильные, что они могут оторвать электроны от атома. На самом деле электрические поля, с которыми люди сталкиваются в повседневной жизни, с большим запасом удовлетворяют этим условиям. Таким образом, изолятор состоит из нейтральных (имеющих нулевой суммарный заряд) частиц. Но если молекулы электронейтральны, то хочется сделать вывод, что диэлектрик не искажает электрическое поле. Это не совсем так. На самом если система электрически нейтральна, то это совсем не означает, что она не создает электрическое поле и с этим полем не взаимодействует. Чтобы понять, как ведет себя электрически нейтральная частица, рассмотрим объект, который называется электрическим диполем. По определению «электрическим диполем называется система двух одинаковых по величине и разных по знаку зарядов разделенных некоторым расстоянием l.»При этом интерес представляет поле на расстояниях L значительно превышающих расстояние между зарядами (см. Рис.1) ). В свою очередь молекулы состоят из атомов. Для наших целей достаточно считать, что атом состоит из положительно заряженного ядра и электронов, суммарный заряд которых отрицательный и в точности равен заряду ядра. Таким образом, атом, и как следствие молекула, (объект, состоящий из нескольких атомов) являются электрически нейтральными объектами. Мы будем рассматривать электрические поля не насколько сильные, что они могут оторвать электроны от атома. На самом деле электрические поля, с которыми люди сталкиваются в повседневной жизни, с большим запасом удовлетворяют этим условиям. Таким образом, изолятор состоит из нейтральных (имеющих нулевой суммарный заряд) частиц. Но если молекулы электронейтральны, то хочется сделать вывод, что диэлектрик не искажает электрическое поле. Это не совсем так. На самом если система электрически нейтральна, то это совсем не означает, что она не создает электрическое поле и с этим полем не взаимодействует. Чтобы понять, как ведет себя электрически нейтральная частица, рассмотрим объект, который называется электрическим диполем. По определению «электрическим диполем называется система двух одинаковых по величине и разных по знаку зарядов разделенных некоторым расстоянием l.»При этом интерес представляет поле на расстояниях L значительно превышающих расстояние между зарядами (см. Рис.1)
Рис.1 Из рисунка видно, почему поле диполя не равно нулю в точке задаваемой вектором
здесь С учетом этого соотношения имеем где введено обозначение для дипольного момента Отсюда легко найти модуль напряженности электрического поля:
Ну а как себя ведет диполь в электрическом поле. Рассмотрим случай постоянного поля (для понимания этого будет достаточно). На Рис.2 показаны силы, действующие на диполь в постоянном электрическом поле. Из этого рисунка видно, что на диполь в электрическом поле действует пара сил, которая стремится развернуть диполь. Момент, который, создает эта пара сил, равен
Вернемся к молекулам, из которых состоит диэлектрик. Можно вычислить среднее положение отрицательных и положительных зарядов:
Нас будут интересовать макроскопические поля, т.е. поля, усредненные по некоторому объему, намного большему, чем объем молекулы (попробуйте сделать чувствительную часть прибора размером с молекулу). Таким образом, если у молекулы средние положения отрицательных и положительных зарядов не совпадают Несмотря на то, что такие молекулы имеют собственный дипольный момент, какое-то количество вещества из этих молекул дипольным моментом не обладает. Это происходит из-за того, что молекулы ориентированны произвольно. Больше того взаимодействие молекул между собой стремится так ориентировать молекулы, что каждое направление оказывается равновероятным. Таким образом, в отсутствии внешнего электрического поля некоторый объём вещества обладает нулевым дипольным моментом, независимо от того, состоит это вещество из полярных или неполярных молекул. Если приложить внешнее электрическое поле, то у объёма диэлектрика появится некоторый дипольный момент. Почему это происходит у неполярных молекул. Дело в том, что внешнее электрическое поле стремится растащить положительные и отрицательные заряды в разные стороны. Чтобы совсем растащить эти заряды (т.е. разрушить молекулу) нужны насколько слишком поля, которые не встречаются в повседневной жизни. Поэтому молекула немного деформируется (вытягивается по направлению поля) и, оказывается
На Рис. 2(a) показано возникновение поляризации в диэлектрике, состоящем из неполярных молекул, а на Рис. 2(b) в диэлектрике, состоящем из полярных молекул. Дипольный момент некоторого объёма диэлектрика пропорционален этому объему и приложенному полю. Для характеристики влияния поля на диэлектрик вводят дипольный момент
где сумма вычисляется по всем молекулам, попавшим в выделенный объем. Величина где Электрическое поле в диэлектрике. Электрическое смещение. Теперь, когда мы так много знаем о строении диэлектриков, перейдем к изучению вопроса о том, как изменится поле внутри диэлектрика, если этот диэлектрик внести в какое-то внешнее поле. Начнем с того, что реальное поле в диэлектрике меняется очень сильно при переходе одной молекулы к другой и внутри молекулы. Такие изменения происходят на масштабах порядка нескольких ангстрем (напомним, что где
Рис.3 Диэлектрик представляющий собой параллельную бесконечную пластину находится в однородном поле всё бы хорошо, да вот поверхностной плотности зарядов В дальнейших выкладках мы будем пользоваться связью вектора поляризации с величиной поля (8). После этого не составляет труда найти поле в диэлектрике: отсюда находим: где величина Тогда для рассмотренного выше примера имеем:
Получается, что в нашем примере вектор электрической индукции не изменяется вне и внутри диэлектрика, ну а напряженность электрического поля вычисляется по формуле (13). Позже, мы убедимся, что не всегда поле в диэлектрике находится так просто. Но ещё раз отметим, что в случае, когда поверхность диэлектрика совпадает с эквипотенциальной поверхностью, то это так. Мы уже говорили, что для потока электрического вектора имеется теорема Гаусса: Мы получили эту теорему, рассматривая поле точечного заряда и потом применяя принцип суперпозиции. Предположим, что заряды помешены в бесконечную диэлектрическую среду. В таком случае можно считать, что граница диэлектрика совпадает с эквипотенциальными поверхностями и Итак, в простейшем случае, когда граница диэлектрика совпадает с эквипотенциальными поверхностями (Если имеется симметрия, то это легко проверяется) можно найти вектор |
||||||||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 1265. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |

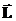 . Да потому, что положительный и отрицательный заряд находятся на разных расстояниях от этой точки (разница небольшая поскольку
. Да потому, что положительный и отрицательный заряд находятся на разных расстояниях от этой точки (разница небольшая поскольку  ). Чтобы получить ответ для потенциала и электрического поля диполя поместим начало координат в центре между зарядами и запишем потенциал, создаваемый диполем в точке задаваемой радиус-вектором
). Чтобы получить ответ для потенциала и электрического поля диполя поместим начало координат в центре между зарядами и запишем потенциал, создаваемый диполем в точке задаваемой радиус-вектором 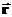 :
: (1)
(1) — радиус вектор положительного заряда, а
— радиус вектор положительного заряда, а  — радиус вектор отрицательного заряда. Из рисунка 1 видно, что
— радиус вектор отрицательного заряда. Из рисунка 1 видно, что 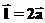 . В принципе эта формула дает правильный ответ для потенциала диполя, но она сложная потому, что содержит маленькие слагаемые в сумме с большими слагаемыми (т.е. не учитывается условие
. В принципе эта формула дает правильный ответ для потенциала диполя, но она сложная потому, что содержит маленькие слагаемые в сумме с большими слагаемыми (т.е. не учитывается условие  ). Воспользуемся следующей цепочкой приближений (которые выполняются с очень хорошей точностью):
). Воспользуемся следующей цепочкой приближений (которые выполняются с очень хорошей точностью):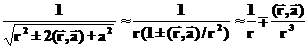 (2)
(2) (3)
(3) . Итак величина поля создаваемого диполем сильно зависит от его ориентации, определяется величиной дипольного момента и убывает с расстоянием быстрее, чем поле точечного заряда. Напряженность электрического поля находится по потенциалу с помощью стандартной процедуры
. Итак величина поля создаваемого диполем сильно зависит от его ориентации, определяется величиной дипольного момента и убывает с расстоянием быстрее, чем поле точечного заряда. Напряженность электрического поля находится по потенциалу с помощью стандартной процедуры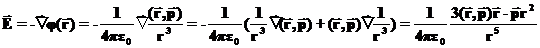 (4)
(4) (5)
(5)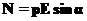 .
.
 (6)
(6) , то такая молекула может рассматриваться как диполь с дипольным моментом
, то такая молекула может рассматриваться как диполь с дипольным моментом  . Где
. Где  — суммарный заряд электронов или ядер (они по модулю равны). Симметричные молекулы (
— суммарный заряд электронов или ядер (они по модулю равны). Симметричные молекулы (  ) в отсутствии внешнего электрического поля не имеют собственного дипольного момента (
) в отсутствии внешнего электрического поля не имеют собственного дипольного момента (  ) и называются неполярными. У ассиметричных молекул (
) и называются неполярными. У ассиметричных молекул (  ) средние положения отрицательного и положительного зарядов, как правило, не совпадают
) средние положения отрицательного и положительного зарядов, как правило, не совпадают  . Такие молекулы называются полярными и обладают собственным дипольным моментом.
. Такие молекулы называются полярными и обладают собственным дипольным моментом.
 , отнесенный к единице объема:
, отнесенный к единице объема: (7)
(7) называется вектором поляризации (иногда, этот вектор называют поляризованностью) диэлектрика. Для широкого интервала напряженностей электрического поля (напряженности, которые встречаются в повседневной жизни) поляризация диэлектрика пропорциональна напряженности электрического поля. Для изотропного диэлектрика связь вектором поляризации и напряженности поля записывают в следующем виде:
называется вектором поляризации (иногда, этот вектор называют поляризованностью) диэлектрика. Для широкого интервала напряженностей электрического поля (напряженности, которые встречаются в повседневной жизни) поляризация диэлектрика пропорциональна напряженности электрического поля. Для изотропного диэлектрика связь вектором поляризации и напряженности поля записывают в следующем виде: (8)
(8) — называется диэлектрической восприимчивостью диэлектрика и зависит только от свойств диэлектрика (находится в таблицах) и не зависит от напряженности поля.
— называется диэлектрической восприимчивостью диэлектрика и зависит только от свойств диэлектрика (находится в таблицах) и не зависит от напряженности поля. (9)
(9) и
и 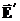 поля создаваемые свободными и связанными зарядами. Из Рис. 2 видно, что плотность связанных зарядов внутри диэлектрика равна нулю (не могут отрицательные и положительные заряды в молекуле сильно разойтись). С другой стороны из Рис.2 можно заключить, что связанные заряды создают некоторую поверхностную плотность зарядов
поля создаваемые свободными и связанными зарядами. Из Рис. 2 видно, что плотность связанных зарядов внутри диэлектрика равна нулю (не могут отрицательные и положительные заряды в молекуле сильно разойтись). С другой стороны из Рис.2 можно заключить, что связанные заряды создают некоторую поверхностную плотность зарядов  . Покажем, как поверхностная плотность зарядов изменяет поле внутри диэлектрика. Для этого рассмотрим конфигурацию поля и диэлектрика показанную на Рис. 3.
. Покажем, как поверхностная плотность зарядов изменяет поле внутри диэлектрика. Для этого рассмотрим конфигурацию поля и диэлектрика показанную на Рис. 3.
 направленном перпендикулярно плоскости пластинки. Поле внутри диэлектрика изменяется за счет поверхностных зарядов, которые на разных гранях отличаются знаком. Т.е. дополнительное поле в диэлектрике создается двумя бесконечными пластинами с противоположной плотностью поверхностных зарядов. Такая система создает нулевое поле вне плоскостей и вдвое большее, чем от одной пластины поле между плоскостями (Это мгновенно следует из принципа суперпозиции). Таким образом, можно написать, что поле в диэлектрике равно:
направленном перпендикулярно плоскости пластинки. Поле внутри диэлектрика изменяется за счет поверхностных зарядов, которые на разных гранях отличаются знаком. Т.е. дополнительное поле в диэлектрике создается двумя бесконечными пластинами с противоположной плотностью поверхностных зарядов. Такая система создает нулевое поле вне плоскостей и вдвое большее, чем от одной пластины поле между плоскостями (Это мгновенно следует из принципа суперпозиции). Таким образом, можно написать, что поле в диэлектрике равно: (10)
(10) мы не знаем. Поэтому нужно ещё немного поработать. Начнем с того, что посчитаем дипольный момент цилиндра, образующие которого перпендикулярны к граням диэлектрика, а основания совпадают с поверхностями диэлектрика и равны
мы не знаем. Поэтому нужно ещё немного поработать. Начнем с того, что посчитаем дипольный момент цилиндра, образующие которого перпендикулярны к граням диэлектрика, а основания совпадают с поверхностями диэлектрика и равны  . Заряды на каждом из оснований совпадают по модулю
. Заряды на каждом из оснований совпадают по модулю 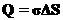 и различаются по знаку. А длина цилиндра, совпадающая с толщиной пластинка равна расстоянию между зарядами. Поэтому дипольный момент этого цилиндра равен
и различаются по знаку. А длина цилиндра, совпадающая с толщиной пластинка равна расстоянию между зарядами. Поэтому дипольный момент этого цилиндра равен 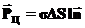 . С другой стороны можно вычислить дипольный момент цилиндра исходя из его объема
. С другой стороны можно вычислить дипольный момент цилиндра исходя из его объема  и вектора поляризации
и вектора поляризации  . Отсюда следует, что:
. Отсюда следует, что: (11)
(11) (12)
(12) (13)
(13) называется диэлектрической проницаемостью изолятора (среды, диэлектрика). Из формулы (13) видно, что поле в среде уменьшается в
называется диэлектрической проницаемостью изолятора (среды, диэлектрика). Из формулы (13) видно, что поле в среде уменьшается в  раз. На самом деле так бывает не всегда, но когда граница диэлектрика совпадает с эквипотенциальной поверхностью это так. При описании поля в диэлектриках широко используется вектор электрического смещения (вектор электрической индукции)
раз. На самом деле так бывает не всегда, но когда граница диэлектрика совпадает с эквипотенциальной поверхностью это так. При описании поля в диэлектриках широко используется вектор электрического смещения (вектор электрической индукции)  , который в некотором смысле (скоро скажем в каком) нечувствителен к связанным зарядам, и определяется следующим выражением:
, который в некотором смысле (скоро скажем в каком) нечувствителен к связанным зарядам, и определяется следующим выражением: (14)
(14) ,
,  и соответственно
и соответственно 
 и
и  (15)
(15) , где
, где 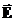 - электрическое поле в отсутствии диэлектрика. А для вектора электрической индукции можно написать:
- электрическое поле в отсутствии диэлектрика. А для вектора электрической индукции можно написать: (16)
(16)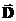 , используя уравнение (15) и не обращая внимания на связанные заряды в диэлектрике, а после этого вектор
, используя уравнение (15) и не обращая внимания на связанные заряды в диэлектрике, а после этого вектор