
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Теорема Гюйгенса — Штейнера.Стр 1 из 2Следующая ⇒ Момент импульса и момент силы относительно оси. Момент импульса и момент силы относительно оси используются при описании вращения тела относительно неподвижной оси. Начнем с определения этих понятий. Выберем неподвижную ось и определим момент импульса частицы и момент сил относительно некоторой точки находящейся на этой оси. Моментом импульса частицы относительно этой оси, называется проекция момента импульса на эту ось (ещё раз подчеркнем, что точка относительно которой определяется момент). Аналогично определяется момент силы относительно некоторой оси. Итак, остановимся несколько подробнее на моменте сил относительно некоторой оси. Для вычисления момента импульса сил относительно оси удобно представить радиус-вектор и силу в виде составляющих (
При таком разбиении момент силы записывается в виде:
Проанализируем входящие в это равенство слагаемые:
В итоге получаем (выбранная ось совпадает с осью Z):
Направление проекции момента силы на ось Z определяется правилом правого винта, а величина равна
Где

Аналогично моменту силы относительно оси можно определить и момент импульса относительно оси. Вращение вокруг неподвижной оси. Момент инерции тела вращающегося вокруг фиксированной оси. Теорема Гюйгенса — Штейнера. Остановимся на выражении для момента импульса твердого (недеформируемого) тела, которое вращается вокруг фиксированной оси. Прежде всего, разобьем тело на маленькие объемы, которые будем считать материальными точками. Пронумеруем эти объёмы и воспользуемся выражением для связи скорости материальной точки вращающейся вокруг
здесь
Поскольку частицы движутся по окружностям лежащим в плоскости перпендикулярной к оси вращения, то плечо i – ой точки равно радиусу окружности
Введенная здесь величина
С учетом этого определения получаем уравнения для вращения вокруг оси Z :
Где
Или, если Часто бывает легко вычислить момент инерции тела относительно оси проходящей через некоторую точку. Рассмотрим две параллельные ось проходящие через точки
При этом имеется связь:
Поскольку точка
Действительно, это равенство означает, что координата центра масс совпадает с началом координат. С учетом (28) — (30) можно преобразовать (27) к следующему виду:
Полученная связь моментов инерции носит название теоремы Гюйгенса — Штейнера (иногда просто Штейнера). |
||||||||||||||||||||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 177. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 ), направленных вдоль оси, относительно которой вычисляется момент и составляющих перпендикулярных этой оси (
), направленных вдоль оси, относительно которой вычисляется момент и составляющих перпендикулярных этой оси (  ):
):


 — равен нулю, т.к. оба вектора параллельны (или антипараллельны).
— равен нулю, т.к. оба вектора параллельны (или антипараллельны).  и
и  — направлены перпендикулярно выбранной оси и поэтому дают нулевой вклад в проекцию на эту ось.
— направлены перпендикулярно выбранной оси и поэтому дают нулевой вклад в проекцию на эту ось. — направлен вдоль выбранной оси, и только он представляет интерес (дает ненулевую проекцию).
— направлен вдоль выбранной оси, и только он представляет интерес (дает ненулевую проекцию).
 .
.
 — плечо силы, которое определяется как кратчайшее расстояние между направлением силы и осью Z (см. Рис.3).
— плечо силы, которое определяется как кратчайшее расстояние между направлением силы и осью Z (см. Рис.3).
 .
.
 — радиус окружности, по которой вращается i – я материальная точка. Очевидно, что угловая скорость имеет одну и ту же величину для всех точек тела (чтобы все точки тела повернулись на один и тот же угол за данный промежуток времени). Соответственно импульс i – ой материальной точки:
— радиус окружности, по которой вращается i – я материальная точка. Очевидно, что угловая скорость имеет одну и ту же величину для всех точек тела (чтобы все точки тела повернулись на один и тот же угол за данный промежуток времени). Соответственно импульс i – ой материальной точки: .
.
 .
.
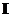 называется моментом инерции относительно оси Z. Она является характеристикой тела и, как видно из (22) момент инерции относительно оси по определению равен:
называется моментом инерции относительно оси Z. Она является характеристикой тела и, как видно из (22) момент инерции относительно оси по определению равен: .
.
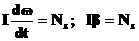 (24)
(24) — угловое ускорение. Внимание! Это уравнение справедливо, только если момент импульса остается постоянным. В общем виде уравнение имеет вид
— угловое ускорение. Внимание! Это уравнение справедливо, только если момент импульса остается постоянным. В общем виде уравнение имеет вид (25)
(25) , то:
, то: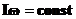 (26)
(26) и
и  . Будем считать, что точка
. Будем считать, что точка  (27)
(27) (28)
(28)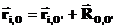 (29)
(29) (30)
(30) (31)
(31)