
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
При помощи крутильных колебанийСтр 1 из 2Следующая ⇒ Лабораторная paбoтa N5 Определение моментов инерции твердого тела при помощи крутильных колебаний
Цель: Изучение законов вращательного движения Задача:экспериментальная проверка теоремы Гюйгенса-Штейнера Оборудование крутильный маятник ФПМ-05, твердое тело в форме параллелепипеда, линейка, штангенциркуль (или микрометр)
Эксперимент заключается в сравнении данных теоретического расчета с экспериментально определяемыми значениями момента инерции тел, а также проверке справедливости формулы Гюйгенса-Штейнера для тела в форме параллелепипеда: Jab =J00 +md2 где J00 - момент инерции тела относительно оси, проходящей через центр масс; Jab момент инерции тела относительно оси, параллельной предыдущей оси и отстоящей от 00’ на расстоянии d, m - масса тела.
где f в свою очередь связан с модулем сдвига G, а также с геометрическими данными проволоки: радиусом R и длиной L
Т.о., зная характеристики проволоки и период колебаний, можно определить момент инерции тела J. Краткая теория: Моментом инерции системы (тела) относительно оси вращения называется физическая величина, равная сумме произведения масс пматериальных точек на квадраты их расстояний r до рассматриваемой оси: В случае непрерывного распределения масс эта сумма сводится к интегралу: 
JАВ =J00’+ md2 (5)
Крутильный маятник – это система, совершающая крутильные (поворотные) колебания (см. рис. 5) Крутильные колебания возбуждаются за счет действия упругих сил, возникающих при деформации кручения, к которой прикреплено колеблющееся тело (см. рис. 5). Период крутильных колебаний определяется моментом инерции и модулем кручения проволоки по формуле (1) Описание экспериментальной установки:
На основании установки располагается электрический миллисекундомер. На передней панели миллисекундомера имеется табло «периоды» (количество периодов или число колебаний) и табло «время» (отсчет времени ведется в секундах), а также кнопки «СЕТЬ», «СБРОС» и «СТОП». Электрический миллисекундомер дает показания количества колебаний N и времени колебаний, по которым можно вычислить период крутильных колебаний маятника. К основанию также крепится колонка, на которой установлены верхний, средней и нижний кронштейны. Крутильный маятник состоит из рамки и стальной проволоки. В рамку вставляется тело-параллелепипед. Стальная проволока натянута между верхним и нижним кронштейнами на ней закреплена рамка. На среднем кронштейне расположены: электромагнит для фиксации рамки в определенном положении, фотоэлектрический датчик, световой поток которого перекрывает водилка, закрепленная на рамке, и совершающая крутильные колебания. Датчик выдает сигнал на электрический миллисекундомер, находящийся в основании установки. Указания по выполнению работы: Подготовить экспериментальные таблицы: Упр. 1. Определение момента инерцииJoo относительно собственной оси симметрии
Упр.2. Определение момента инерции JАВ при несимметричной оси вращения
Упр.1. Определение момента инерции относительно оси, проходящей через центр масс 1. подключить установку к сети; нажать кнопку "СЕТЬ" и "СБРОС; 2. приблизить водилку к электромагниту и зафиксировать ее. 3. нажать на кнопку "ПУСК", рамка освобождается и начинает колебаться вокруг стальной проволоки, при этом водилка должна пересекать световой поток датчика и миллисекундомер начнет отсчитывать количество периодов и время колебаний; 4. измерьте микрометром или штангенциркулем диаметр проволоки, ее длину, стороны параллелепипеда а, b, с; 5. учитывая модуль сдвига для стальной проволоки G=78,4 Н/м2, определить по формуле (2) модуль кручения крутильного маятника f 6. поместить параллелепипед между неподвижной (нижней) и подвижной (верхней балками рамки, затянуть гайки на зажимных втулках по оси 00’; 7. определить время n колебаний tn по секундомеру, эксперимент повторить 5 раз 8. вычислить среднеарифметическое значение для времени t , и определить период T00’ для колебаний вокруг своей оси симметрии по формуле 9. используя формулу (1), найти экспериментальное значение момента инерции тела для колебаний вокруг своей оси симметрии J00’ 10. считая m = 2кг, вычислить теоретическое значение J00’согласно формуле: Упр.2. Определение момента инерции JАВ при несимметричной оси вращения оси параллельной предыдущей и проверка теоремы Штейнера –Гюйгенса.
1. закрепить параллелепипед по оси, отступающей от центральной оси симметрии на расстояние d ( измерить штангенциркулем). 2. определить период колебаний ТАВ для несимметричного размещения бруска по схеме, аналогичной при определении T00’ в первом упражнении. 3. расcчитать момент инерции параллелепипеда JАВ в случае несимметричного размещения по экспериментальным данным и по теореме Гюйгенса-Штейнера JАВ =J00’+ md2 и сравнить их.
4..дать объяснение полученным результатам.
Контрольные вопросы: 1. Величины, характеризующие вращательное движение. 2. Основной закон динамики вращательного движения 3. Момент инерции и момент силы 4. Моменты инерции простейших геометрических тел 5. Закон Гука для линейных и крутильных деформаций 6. Что представляет собой крутильный маятник в данной установке? 7. Связь между периодом крутильных колебаний и моментом инерции маятника. 8. Сформулируйте и докажите теорему Гюйгенса-Штейнера. 9. Определение момента инерции. Является ли момент инерции постоянной величиной для заданной материальной точки или твердого тела? 10. Кинетическая энергия вращения твердого тела
Литература: 1. Обшая физика: Руководство полабораторному практикуму./Под ред. Крынецкого И.Б. и Струкова Б.А. – М.: ИНФРА-М, 2008. 2. Архангельский М.М. Курс физики. Механика, изд.2,испр.и доп.-М.:Просвещение.- 1965. 3. Фриш С. Э., Тиморева А. В. Курс общей физики, т. 1. Физические основы механики Молекулярная физика. Колебания и волны. М., Физматгиз. 1962 4. Практикум по общей физике. Под ред. Проф. В. Ф. Ноздрева М.:Просвещение.-1971 5. Лабораторный практикум по общей физике. Механика. /Под ред.А.Н.Капитонова. - Якутск: изд-во ЯГУ.-1988 . ПРИЛОЖЕНИЕ 1 ВРАЩАТЕЛЬНОЕ ДВИЖЕНИЕ
Для вращательного движения существуют величины, уравнения движения и формулы, аналогичные существующим для поступательного движения.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 691. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 Положение всех осей указано на рис.1. Как известно, период крутильных колебаний Т связан с моментом инерции J и модулем кручения проволоки f по формуле:
Положение всех осей указано на рис.1. Как известно, период крутильных колебаний Т связан с моментом инерции J и модулем кручения проволоки f по формуле: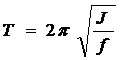 , (1) (рабочая формула)
, (1) (рабочая формула) (2) (см. приложение 2)
(2) (см. приложение 2) (3)
(3) (4)
(4)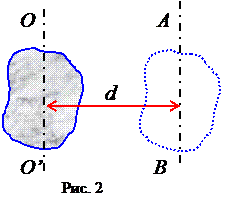 Теорема Гюйгенса-Штейнера: момент инерции тела J0’0’ относительно любой оси вращения АВ равен сумме момента его инерции J00’, относительно параллельной оси 00’, проходящей через центр масс тела, и произведению массы тела на квадрат расстояния dмежду осями АВ и 00’ (см. рис.2)
Теорема Гюйгенса-Штейнера: момент инерции тела J0’0’ относительно любой оси вращения АВ равен сумме момента его инерции J00’, относительно параллельной оси 00’, проходящей через центр масс тела, и произведению массы тела на квадрат расстояния dмежду осями АВ и 00’ (см. рис.2)
 Крутильный маятник ФПМ-05 - это настольная установка (см. рис. 6)
Крутильный маятник ФПМ-05 - это настольная установка (см. рис. 6)
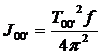
 и сравнить с экспериментально определенным значением J00’
и сравнить с экспериментально определенным значением J00’