
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Использование критериев для оценки колеблимости изучаемого признака»Средние величины — это количественная обобщающая характеристика однородной совокупности с изменяющимся варьирующим признаком. Они используются при оценке физиологических показателей (средняя частота пульса, дыхания, АД), параметров физического развития (средний рост юношей 18 лет, средняя масса тела), для санитарно-гигиенических характеристик (средняя жилая площадь на одного человека, среднее число бактерий в 1 мл), при количественном описании медицинских услуг (среднее число посещений в час, средняя занятость койки в течение года). Вариационный ряд – статистический ряд распределения значения изучаемого количественного признака, расположенных в порядке убывания или возрастания. Вариационные ряды бывают: 1) простыми; 2) взвешенными; 3) сгруппированными и несгруппированными; 4) одномодальными и мультимодальными; 5) симметричными и несимметричными; 6) дискретными и непрерывными; 7) четными и нечетными.
Мода (Мо) — средняя величина, обозначающая варианту с наибольшей частотой повторения. Медиана (Ме) — варианта, занимающая срединное положение во взвешенном вариационном ряду. Задача 1.2
где a = V – A; d = V – M 
1. Мода (Мо) = А = 6 2. Медиана (Ме) = 7, т.к. 38/2 = 19 (значение 19 наблюдения равно 6) 3. Средняя арифметическая (М)
а). М =
б). М = А + Вывод: так как мода, медиана и среднее арифметическое (вычисленное двумя способами) близки по значению, данный ряд является симметричным.
Критерии разнообразия:
1. Лимит Lim = Vmax ÷ Vmin Lim = 13 ÷ 4 2. Амплитуда Ampl = Vmax – Vmin Ampl = 13 – 4 = 9 3. Среднее квадратическое отклонение (σ) (σ) =± 4. Коэффициент вариации (СV) = Критерии оценки коэффициента вариации:
Вывод: в данном случае наблюдается сильное колебание признака.
Правило трёх сигм: В симметричном вариационном ряде: в пределах М± σ должно находиться 68,37% вариант в пределах М± 2σ должно находиться 95,5% вариант в пределах М± 3σ должно находиться 99,7% вариант
Если первое правило выполняется, то последующие можно не проверять M ± σ = 7,26 ± 3,25 = 4,01 ÷ 10,51
В данный интервал попадает 29 случая
М± σ = 76,3% (показатель более 68,37%) – правило выполняется.
Вывод: данный вариационный ряд является взвешенным, дискретным, одномодальным, симметричным, чётным, подчиняется правилу трёх сигм. Критерии достоверности 1. Ошибка репрезентативности:
2. Доверительный интервал: Mген = Мвыб ± tm, где Мвыб = М
При t = 2 и при вероятности безошибочного прогноза 95% Mген = 7,26 ± 2 × 0,52 = 7,26 ± 1,04 = 6,22 ÷ 8,3 Вывод: с вероятностью безошибочного прогноза 95% можно утверждать, что длительность случаев нетрудоспособности в связи с ОРЗ и гриппом у рабочих основных профессий будет находиться в пределах от 6,22 – до 8,3 дней.
При t = 3 и при вероятности безошибочного прогноза 99% Mген = 7,26 ± 3 × 0,52 = 7,26 ± 1,56 = 5,7 ÷ 8,82
Вывод: с вероятностью безошибочного прогноза 99% можно утверждать, что длительность случаев нетрудоспособности в связи с ОРЗ и гриппом у рабочих основных профессий будет находиться в пределах от 5,7 – до 8,82 дней.
3. Критерий Стьюдента: Оцените достоверность различия полученного показателя и средней длительности ОРЗ и гриппа у рабочих вспомогательных производств, где она составила 7,2 ± 0,01 дня. Средняя длительность одного случая нетрудоспособности у рабочих основных профессий по результатам исследования составила 7,26 ± 0,52 дня.
где t – критерий Стьюдента М1 и М2 – сравниваемые средние величины m1 и m2 – ошибки репрезентативности
Вывод: так как t < 2, то различия показателей длительности случаев нетрудоспособности для рабочих основных и вспомогательных профессий по критерию Стьюдента недостоверны. «Стандартизация» Метод стандартизации используется при оценке показателей здоровья только при сравнении их уровней. Этот метод расчета условных величин применяется для устранения неоднородности состава сравниваемых совокупностей. Он показывает, какой был бы уровень показателей, если бы состав сравниваемых совокупностей был бы одинаков. А также помогает установить причину разных уровней показателей.
Способы:
Задача 1.3
На основании табличных данных вычислите стандартизованные показатели плодовитости в районах А и Б, сделайте выводы. За стандарт принять возрастной состав женщин района Б.
I Расчёт интенсивных показателей и общих в районах А и Б
Район А
Район Б
II Расчёт специальных интенсивных коэффициентов для районов А и Б
Район А
Район Б
III Расчёт ожидаемых величин рождаемости
Район А
Район Б
IV Расчет стандартизованных коэффициентов
Район А
Район Б
Вывод: если бы возрастной состав женщин в районах А и Б был бы одинаков, то рождаемость была бы выше в районе Б. Следовательно менее высокий фактический уровень рождаемости в районе А связан с неоднородностью возрастной структуры женщин в районах А и Б.
«Медицинская демография»
Демография – наука о населении, изучающая закономерности явлений и процессов в структуре, размещении и динамике населения с учётом политических, социальных, экономических, биологических и других факторов.
Статика населения Динамика населения
v численность v структура v размещение Механическая v эмиграция v иммиграция v маятниковая v челночная v урбанизация Естественная v рождаемость v смертность v естественный прирост v средняя продолжительность предстоящей жизни Статика населения – численный состав населения на определенный момент времени по полу, возрасту, семейному положению, национальности, языку, грамотности, социальным и профессиональным группам, а также размещение населения по территории. Статика изучается посредством переписи раз в 5 – 10 лет. В России по данным переписи 2003г проживает 145,2 млн. человек. Динамика населения – движение населения.
Правила выполнения переписи: · периодичность (1 раз в 5-10 лет); · всеобщность; · единство методики; · в период минимальной миграции; · опросный метод; · централизованный анализ.
Методы расчета численности в межпереписной период:
где Р – искомое число наблюдений, Р1 – численность по первой переписи Р2 – численность по второй переписи t1 – число лет, прошедших от первой переписи до года, на который определяется Р n – число лет между первой и второй переписями
где Р – искомое число наблюдений, Р1 – численность по первой переписи Р2 – численность по второй переписи t2 – число лет, прошедших от последней переписи до года, на который определяется Р n – число лет между первой и второй переписями На основании расчета удельного веса лиц в возрасте от 14, от 15 до 49 и старше 50 лет определяется возрастной тип населения:
Рождаемость =
Коэф. фертильности =
Младенческая см. =
Младенческая см. =
Неонатальная см. =
Ранняя неонатальная см. =
Поздняя неонатальная см. =
Постнеонатальная см. =
Перинатальная с. =
Мертворождаемость =
Естественный прирост = Рождаемость – Общая смертность
Задача 1.2
В районе К. численность населения в 2007г. составила 85000 человек (в 2006 – 85500 человек), из них в возрасте от 0 до 14 лет – 20000, 15 – 49 – 20000, старше 49 – 30000. Число женщин – 46000, в т.ч. детородного возраста – 16500. В 2007г. родилось живыми 1810 детей (в 2006 – 1836), умерло – 600 человек, в т.ч. детей до года 56. Число мертворождённых – 10 в т.ч. антенатально умерли – 7. Умерло детей на I неделе жизни – 9, на I месяце – 16. Среди детей, умерших в возрасте до I года (56), умерло от пневмонии – 19, от желудочно-кишечных заболеваний – 16, болезней новорождённых – 20, от прочих заболеваний – 1.
Решение: 1. Показатели статики · Определение процентного соотношения возрастных групп и определение типа возрастной структуры населения.
Вывод: структура населения по возрасту в районе К. на 2007г.: 23,5 % приходится на лица в возрасте от 0 до 14 лет; 41,2 % приходится на лица в возрасте от 15 до 49 лет; 35,3 % приходится на лица в возрасте старше 49 лет. Для определения типа возрастной структуры населения сравниваем две возрастные группы: от 0 до 14 лет и старше 49 лет (23,5 % < 35,3 %). Таким образом, в районе К. тип возрастной структуры – регрессивный.
а). Мужское население
б). Женское население
Вывод: структура населения по полу в районе К. 45,8 % приходится на население мужского пола 54,2 % приходится на население женского пола
2. Показатели динамики
Вывод: рождаемость в районе К. на 2007г. составила 21,3 ‰, что соответствует среднему уровню. Уровень рождаемости в районе К. выше, чем в России.
Вывод: общая смертность в районе К. на 2007г. составила 7 ‰, что соответствует низкому уровню. Уровень смертности в районе К. ниже, чем в России.
Вывод: в районе К. зарегистрирован положительный естественный прирост населения.
Вывод: младенческая смертность в районе К. на 2007г. составила 30,9 ‰, что соответствует высокому уровню.
Ø Мертворождаемость
Ø Неонатальная смертность
Вывод: показатель в районе К. ниже, чем в России
Ø Ранняя неонатальная смертность
Вывод: показатель в районе К. ниже, чем в России
Ø Поздняя неонатальная смертность
Ø Постнеонатальная смертность
Вывод: показатель в районе К. выше, чем в России
Ø Перинатальная смертность
«Метод корреляции» Метод корреляции позволяет установить наличие связи: – форму связи; – силу связи; – направление. Формы связи: 1. Функциональная – при которой каждому значению одного признака соответствует только одно строго определённое значение другого признака. 2. Корреляционная – при которой каждому значению одного признака может соответствовать несколько значений другого, взаимосвязанного с ним признака. Значение коэффициента корреляции от – 1 до + 1. Связь в зависимости от знака коэффициента корреляции может быть прямой (положительной) или обратной (отрицательной). Виды связи в зависимости от коэффициента корреляции: Ø 0 – связь отсутствует Ø ≤ 0,3 – слабая корреляционная связь Ø 0,3 – 0,7 – средняя корреляционная связь Ø 0,7 – сильная корреляционная связь Ø 1 – полная (функциональная) Существует несколько способов расчета коэффициента корреляции:
Задача 1.4 Путём вычисления коэффициента ранговой корреляции Спирмена определить характер и размер связи между уровнем мертворождаемости и весом ребёнка при рождении.
ρ = 1 – Вывод: установлена функциональная связь.
Задача 1.5
Определить коэффициент корреляции Пирсона, сделать выводы
Результаты определения потребного количества калорий в сутки в зависимости от веса, у девочек 8 лет
rxy = Вывод: связь корреляционная, сильная, обратная Определение представительности коэффициента корреляции: Представительность коэффициента корреляции может быть определена по его средней ошибке, которую можно вычислить по формуле: m = ± Коэффициент корреляции достоверен в том случае, если он превышает свою ошибку в 3 и более раз. Это условие в данном случае не выполняется. Оценка значимости по t–критерию: t = 0,98/0,33 = 2,96 Так как t > 2, то это говорит о значимости критерия.
Вывод: в результате проведённого анализа полученных данных можно говорить о наличии сильной и обратной взаимосвязи между средним весом 8-летних девочек и потребным количеством калорий в сутки. При расчете и оценке коэффициента Пирсона вычислили его ошибку: т.к. она не более чем в 3 раза меньше самого коэффициента, можно говорить о недостоверности данного коэффициента. Также была проведена оценка значимости по t–критерию: т.к. t > 2, можно говорить о значимости полученных результатов. Таким образом, можно говорить о недостаточной достоверности влияния веса 8-летних девочек на потребное количество калорий в сутки и о значимости полученных результатов. «Заболеваемости населения. Методика и практическое изучение. 5 видов заболеваемости» Заболеваемость – показатель, характеризующий распространённость, структуру, динамику зарегистрированных болезней среди населения в целом или в отдельных группах. Эти показатели служат также для оценки работы врача, медицинского учреждения и органов здравоохранения в целом.
Выделяют:
Заболеваемость подразделяют на 5 групп:
По методу исследования а) по данным обращаемости б) по данным медицинских осмотров (предварительных, периодических, целевых медосмотров)
а) инфекционной природы (туберкулёз, венерические заболевания, микроспория, трахома) б) неинфекционные (психические, онкологические, заболевания системы кровообращения, наркомании, алкоголизм)
Задача 1.2
Наиболее крупным промышленным предприятием района является сельский домостроительный комбинат, где работают 765 человек. В 2007г. трудопотери рабочих от заболеваемости с временной утратой трудоспособности составили 540 случаев и 4290 дней. В структуре заболеваний болезни органов дыхания составили 280 случаев, болезни костно-мышечной системы – 85 случаев, болезни нервной системы – 60 случаев, травматизм – 50, прочие болезни – 65. Ни разу в течение года не болело 125 человек.
1. Болезни органов дыхания
2. Болезни костно-мышечной системы
3. Болезни нервной системы
4. Травматизм
5. Прочие болезни
Вывод: в структуре заболеваний с временной утратой трудоспособности первое место занимают болезни органов дыхания (51,8% случаев), второе место – болезни костно-мышечной системы (15,7% случаев), третье место – прочие болезни (12%), четвёртое место – болезни нервной системы (11,1% случаев), пятое место – травматизм (9,2% случаев). «Критерий согласия Хи-квадрат» Критерий согласия Хи-квадрат (χ2) – используется для оценки эффективности проводимых мероприятий. Основан на использовании «нулевой гипотезы». Статистическое сравнение двух выборок, изучаемый признак в которых представлен частотой этого признака в абсолютных, а не в относительных величинах, производится с помощью критерия согласия χ2. И вычисляется по формуле: χ2= Можно использовать 2 метода: — метод 4 полей — метод введения «нулевой» гипотезы
Задача 1.6 Используя критерий χ2, определите, является ли наличие отдельной квартиры фактором, способствующим рождению первого ребёнка.
Решение:
Подставляем полученные данные в формулу: χ2=
Проверка полученного результата на достоверность: K = (S – 1) × (R –1) = (2 – 1) × (2 – 1) = 1
При числе степеней K = 1 критерии значения χ2 для условия значимости P = 0,05 равен χ2 = 3,84 Вывод: вычисленное значение χ2 = 2,01, при K = 1 превышает табличное значение χ2, равное 1,32 для уровня значимости 0,25. Следовательно, можно утверждать, что имеется достоверная связь между рождением первенца и наличием отдельной квартиры с вероятностью безошибочного прогноза 75%.
Задача 1.7
С помощью критерия χ2 определите, влияют ли сроки госпитализации больных инфарктом миокарда на исход заболевания.
Решение: Для решения необходимо использовать метод определения критерия χ2 по Руниони. Формула для вычисления имеет следующий вид: χ2=Σ(Р1-Р2)2/Р2 , где P1 – фактическое число, P2 – ожидаемое число
1. Вводим «нулевую» гипотезу, согласно которой срок госпитализации не влияет на исход заболевания. В связи с этой гипотезой допускаем, что распределение признака было одинаково во всех группах. 2. Определение ожидаемых величин:
В 1-й группе
Во 2-й группе
В 3-й группе
3. Подставляем полученные значения в формулу: χ2=Σ(Р1-Р2)2/Р2 =
χ2= 21,012
4. Определение числа степеней свободы: K = (S – 1) × (R –1) = (3 – 1) × (2 – 1) = 2
При числе степеней K = 2 критерии значения χ2 для условия значимости P = 0,01 равен χ2 = 9,21
Вывод: так как вычисленное значение χ2 (21,012) при К = 2 превышает табличное значение χ2 (9,21) при к = 2 для уровня значимости 0,01, то следует отвергнуть «нулевую» гипотезу и можно утверждать, что имеется достоверное влияние сроков госпитализации больных инфарктом миокарда на исход заболевания. «Первичная медико-социальная помощь городскому населению. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 340. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
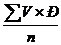 =
=  = 7,26 дней
= 7,26 дней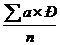 = 6 +
= 6 + 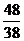 = 7,26 дней
= 7,26 дней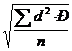 = ±
= ± 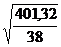 = ± 3,25 дней
= ± 3,25 дней x 100 % =
x 100 % =  = 45 %
= 45 %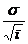

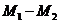
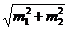
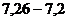
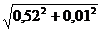

 Демография
Демография




 Общая смертность =
Общая смертность =

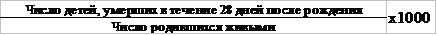





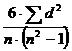 = 1 –
= 1 – 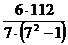 = 1 –
= 1 – 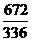 = – 1
= – 1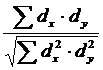 =
= 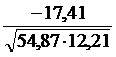 =
= 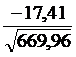 =
=  = – 0,67
= – 0,67 ; m = ±
; m = ± 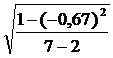 = ±
= ±  = ± 0,33
= ± 0,33
 Число дней ЗВУТ на 100 рабочих =
Число дней ЗВУТ на 100 рабочих = 


 , где a, b, c, d – число наблюдений в разных группах.
, где a, b, c, d – число наблюдений в разных группах.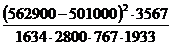 = 2,01
= 2,01