
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
С помощью теоремы об устойчивости по первому приближению исследовать на устойчивость нулевое решение системы ⇐ ПредыдущаяСтр 2 из 2
Решение. Составим якобиан системы:
Теорема 5(о неустойчивости по первому приближению). Пусть функция
Найдем собственные значения матрицы
Полином не является гурвицевым:
Мы имеем один положительное собственное значение, следовательно тривиальное решение системы неустойчиво по Ляпунову.
Проверим наш результат в пакете Maple (Рис. 5.1) >
>
Рис. 5.1 Численное интегрирование системы
Используя теорему Пуанкаре-Бендиксона, доказать существование цикла у системы.
Решение. Сначала, покажем что у системы существует единственное (неустойчивое) состояние равновесия.
Построим якобиан системы:
Найдем собственные значения
Оба собственных значения якобиана положительны, особая точка неустойчива. Рассмотрим функцию Ее производная в силу системы имеет вид:
Значения производной в силу системы меняются при пересечении эллипса
Однако, мы не можем использовать эллипсы для доказательства существования «кольца». Рассмотрим 2 окружности, >

На окружности На каждой окружности возьмем точки, лежащие близко к оси абсцисс и проверим поведение траекторий. Расчеты будем производить при помощи пакета Maple: >
Действительно, по теореме о непрерывной зависимости решений от начальных данных, траектории будут в дальнейшем вести себя подобным образом. Мы можем заявить о существовании цикла у системы. Лемма 6.Если внутри положительно (отрицательно) инвариантной для траекторий системы
Мы доказали, что у системы существует положительно инвариантная область, в которой нет решений системы. По лемме 6, у системы есть цикл.
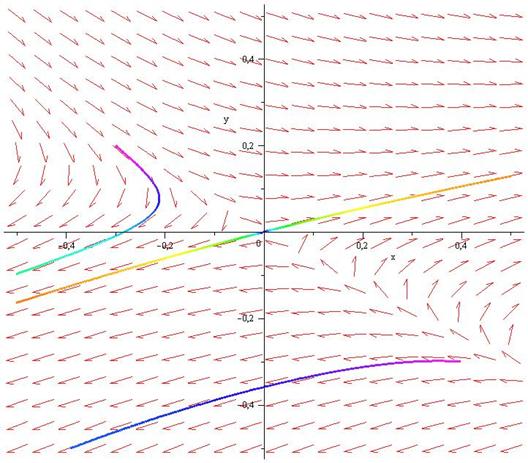
Проверим полученный результат в пакете Maple (Рис. 6.2).
>
>
Рис. 6.2 Численное интегрирование системы
7. Методом Пуанкаре найти приближенно периодические решения дифференциального уравнения
Решение.
Тогда Подставим ряды (7.1) в исходное уравнение
Приравняем коэффициенты при одинаковых степенях параметра
………………………………….. В (7.2) существует 2 решения: 1) Рассмотрим случай Тогда из второго уравнения системы (7.2):
Решение этого уравнения складывается из суммы частного и общего решений. Найдём общее решение:
характеристическое уравнение будет иметь вид:
но период этого решения
Продифференцировав 2 раза, получим
Тогда
Будем искать
Имеем:
Решение будет иметь вид
Тогда, подставляя в уравнение, получим:
Итак, приближенное периодическое решение имеет вид:
Или же:
2) Теперь, рассмотрим случай Тогда из второго уравнения системы (7.2):
Решение этого уравнения складывается из суммы частного и общего решений. Найдём общее решение:
характеристическое уравнение будет иметь вид:
Это решение имеет период
Продифференцировав 2 раза, получим
Тогда
Будем искать
Имеем:
Решение будет иметь вид
Тогда, подставляя в уравнение, получим:
Таким образом, приближенное периодическое решение имеет вид:
Или же: Используя пакет MathCAD, сравним полученные решения с точным решением исходного уравнения на периоде Для
Для
Список литературы:
1. Буркин И.М. Обыкновенные дифференциальные уравнения. Методы интегрирования. Теория устойчивости. Теория колебаний. Тула: ТулГУ, 2004. 2. Федорюк М.В. Обыкновенные дифференциальные уравнения. – 2-е изд., перераб. и доп. – М.: Наука. Главная редакция физико-математической литературы, 1985. – 448 с. 3. Филиппов А. Ф. Сборник задач по дифференциальным уравнениям. - М.: Наука, 1979. - 128 с. 4. Пантелеев А.В., Якимова А.С., Босов А.В.«Обыкновенные дифференциальные уравнения в примерах и задачах». – Москва,2000 5. Тихонов А.Н., Васильева А.Б., Свешников А.Г.«Дифференциальные уравнения». – Москва,2002
|
||||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 473. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |


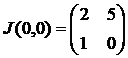
 непрерывно дифференцируема в некоторой окрестности положения равновесия
непрерывно дифференцируема в некоторой окрестности положения равновесия  . Если хотя бы одно собственное значение матрицы Якоби
. Если хотя бы одно собственное значение матрицы Якоби  имеет положительную вещественную часть, то положение равновесия
имеет положительную вещественную часть, то положение равновесия  :
:



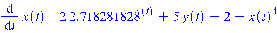



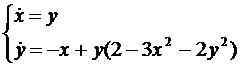


 ;
; ;
; :
: ,
,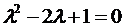 ,
,
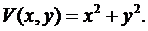
 ;
;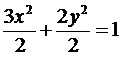
 , которая не пересекает эллипс (6.1) и лежит внутри него, и окружность
, которая не пересекает эллипс (6.1) и лежит внутри него, и окружность  , которая так же не пересекает заданный эллипс, и внутри которой он располагается (Рис. 6.1)
, которая так же не пересекает заданный эллипс, и внутри которой он располагается (Рис. 6.1)

 Рис. 6.1 Эллипс (1), при пересечении которого производная в силу системы меняет знак (красный), окружность
Рис. 6.1 Эллипс (1), при пересечении которого производная в силу системы меняет знак (красный), окружность  , (синяя).
, (синяя).













 области нет состояний равновесия системы, то в этой области содержится по крайней мере один цикл системы.
области нет состояний равновесия системы, то в этой области содержится по крайней мере один цикл системы.







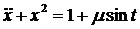
 периодическое решение будем искать в виде ряда по степеням малого параметра, то есть в виде
периодическое решение будем искать в виде ряда по степеням малого параметра, то есть в виде
 (7.1)
(7.1)
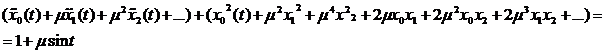
 в левой и правой частях последнего равенства:
в левой и правой частях последнего равенства:

 (7.2)
(7.2)
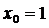 .
.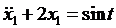 .
.
 . Тогда
. Тогда ,
, , т.е. оно не порождает
, т.е. оно не порождает  -периодических решений, поэтому решение уравнения
-периодических решений, поэтому решение уравнения  будем искать в виде
будем искать в виде .
.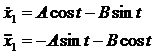

 из третьего уравнения системы (7.2).
из третьего уравнения системы (7.2).
 , или
, или  ,
, .
. .
. 





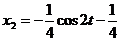 .
. ;
; .
. .
. .
.
 . Тогда
. Тогда .
.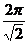 , т.е. оно так же не порождает
, т.е. оно так же не порождает 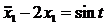 будем искать в виде
будем искать в виде .
.

 ,
, .
. ,
,



 .
. .
.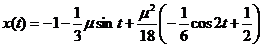
 .
. :
:
 :
: