
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Исследовать устойчивость нулевого решения, построив функцию Ляпунова и применив теоремы Ляпунова или ЧетаеваСтр 1 из 2Следующая ⇒ Курсовая работа по курсу “Дифференциальные уравнения” на тему: “Элементы качественной теории Обыкновенных дифференциальных уравнений и теории колебаний”
Автор работы ___________________ ст. гр. 520191 Ульченков М.А. подпись дата
Руководитель работы ______________ асс. каф. мат.ан. Соболева Д. В. подпись дата
Работа защищена ___________________ Оценка __________________ дата
Тула 2011
Содержание
Пояснительная записка
В данной курсовой работе рассматриваются основные аспекты качественной теории обыкновенных дифференциальных уравнений на примере решения задач, посвященных нахождению особых точек и исследованию их характера для нелинейной автономной системы 2-го порядка; нахождению первого интеграла и построению фазового портрета нелинейного автономного уравнения 2-го порядка; исследованию устойчивости и асимптотической устойчивости нулевого решения линейного однородного уравнения 4-го порядка с постоянными однородного уравнения 4-го порядка с постоянными коэффициентами; построению функции Ляпунова для нелинейной автономной системы 2-го порядка; исследованию асимптотической устойчивости нулевого решения нелинейной автономной системы 2-го порядка с помощью линеаризации правых частей (первого приближения); исследованию диссипативности нелинейной автономной системы 2-го порядка и существовании у нее циклов; приближенному построению с помощью метода малого параметра периодического решения нелинейного неавтономного уравнения 2-го порядка. Особое внимание уделено построению фазовых траекторий в окрестностях особых точек и фазового портрета.  Объем курсовой работы составляет 33 стр.
Найти особые точки системы. Определить их тип. Построить схематически фазовый портрет в окрестностях каждой особой точки. Решение. Для нахождения особых точек, необходимо решить систему Разобьем ее на две:
Таким образом, мы имеем 4 особые точки:
Построим Якобиан системы:
Рассмотрим точки подробнее:
Рис 1.1 Схематический портрет особой точки
Рис 1.2 Схематический портрет особой точки
Для определение направления закручивания, построим вектор направления в окрестностях
Рис 1.3 Схематический портрет особой точки
Рис 1.4 Схематический портрет особой точки
Проверим полученный результат в пакете Maple:
Рис 1.5 Фазовый портрет особой точки
Рис 1.6 Фазовый портрет особой точки
Рис 1.7 Фазовый портрет особой точки
Рис 1.8 Фазовый портрет особой точки
2. Найти первый интеграл. Изобразить фазовый портрет уравнения на плоскости
Решение. Канонический вид уравнения Ньютона:
Оно описывает движение материальной частицы массой
где Для того, что бы найти первый интеграл, умножим обе части уравнения на
следовательно:
Выражение Полагая, что
Найдем особые точки системы:
Таким образом, имеем три особые точки:
Исследуем функцию Функция четная,
Функция обращается в 0 при Производная функции обращается в ноль в особых точках системы.
Таким образом, особая точка
Рис 2.1 Фазовый портрет уравнения на плоскости
Проверим полученный результат в пакете Maple: > restart; with(DEtools):
Рис 2.2 Фазовый портрет уравнения на плоскости
Угловые скорости движения точек по замкнутым фазовым траекториям (вокруг точек типа «центр») могут совпадать (синхронное движение) или же быть различным (асинхронное движение). Для проверки синхронности движения вокруг точек
которая в нашем случае имеет вид:
Варьируя уровень энергии, построим таблицу зависимости периода движения для точек
Таким образом, период вращения вокруг обеих точек зависит от уровня энергии (Рис 2.3), следовательно движение вокруг них является асинхронным. Рис 2.3 График зависимости периода движения вокруг точек > E:=-(0.10); evalf(solve( (((x^4)/2) -((x^2)/2) - E) , x),10);
> a:=simplify((2^(1/2))*int((1/(sqrt(E+(x^2)/2 - (x^4)/2))),x=-0.85..-0.53)); b:=simplify((2^(1/2))*int((1/(sqrt(E+(x^2)/2 - (x^4)/2))),x=0.53..0.85));
> E:=-(0.08); evalf(solve( (((x^4)/2) -((x^2)/2) - E) , x),10);
> a:=simplify((2^(1/2))*int((1/(sqrt(E+(x^2)/2 - (x^4)/2))),x=-0.89..-0.45)); b:=simplify((2^(1/2))*int((1/(sqrt(E+(x^2)/2 - (x^4)/2))),x=0.45..0.89));
> E:=-(0.06); evalf(solve( (((x^4)/2) -((x^2)/2) - E) , x),10);
> a:=simplify((2^(1/2))*int((1/(sqrt(E+(x^2)/2 - (x^4)/2))),x=-0.92..-0.38)); b:=simplify((2^(1/2))*int((1/(sqrt(E+(x^2)/2 - (x^4)/2))),x=0.38..0.92));
> E:=-(0.04); evalf(solve( (((x^4)/2) -((x^2)/2) - E) , x),10);
> a:=simplify((2^(1/2))*int((1/(sqrt(E+(x^2)/2 - (x^4)/2))),x=-0.955..-0.3)); b:=simplify((2^(1/2))*int((1/(sqrt(E+(x^2)/2 - (x^4)/2))),x=0.3..0.955));
> E:=-(0.02); evalf(solve( (((x^4)/2) -((x^2)/2) - E) , x),10);
> a:=simplify((2^(1/2))*int((1/(sqrt(E+(x^2)/2 - (x^4)/2))),x=-0.9789..-0.21)); b:=simplify((2^(1/2))*int((1/(sqrt(E+(x^2)/2 - (x^4)/2))),x=0.21..0.9789));
> E:=-(0.01); evalf(solve( (((x^4)/2) -((x^2)/2) - E) , x),10);
> a:=simplify((2^(1/2))*int((1/(sqrt(E+(x^2)/2 - (x^4)/2))),x=-0.9897..-0.143)); b:=simplify((2^(1/2))*int((1/(sqrt(E+(x^2)/2 - (x^4)/2))),x=0.143..0.9897));
3. Исследовать при каких значениях параметра
Решение.
Мы имеем стандартный полином с коэффициентами
Составим для полинома матрицу Гурвица, и применим критерий Льенара-Шипара:
Следовательно, система асимптотически устойчива при Проверим результат в пакете Maple: > > >
>
>
>
>
Исследовать устойчивость нулевого решения, построив функцию Ляпунова и применив теоремы Ляпунова или Четаева
Решение. Функцию Ляпунова будем искать в виде
Тогда,
Положим, Зададим множество
Теорема 4 (теорема Четаева). Пусть
Очевидно, что на множестве
Проверим полученный результат в пакете Maple (Рис. 4.1)
> restart: with(DEtools): > eq1:=(diff(x(t),t)=(x(t)^5)+(y(t)^3));
> eq2:=(diff(y(t),t)=(x(t)^3)-(y(t)^5));
> DEplot([eq1,eq2],[x(t),y(t)],t=0..50,[[x(0)=0.35, y(0)=-0.39],[x(0)=-0.4, y(0)=0.35], [x(0)=-0.4, y(0)=0.45],[x(0)=0.4, y(0)=-0.4]],x=-0.5..0.5, y=-0.5..0.5, linecolor=sin(t), stepsize=0.01);
Рис. 4.1 Фазовый портрет системы
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 724. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
||||||||||||||||||||||||||||||||||||||||||||||||||||






 .
.
 Тип точки – седло
Тип точки – седло
 Тип точки - седло
Тип точки - седло
 Тип точки – устойчивый фокус
Тип точки – устойчивый фокус



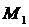










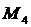








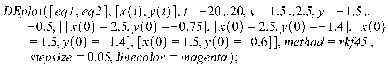





 .
.

 , в потенциальном поле с потенциалом
, в потенциальном поле с потенциалом 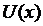 . В нашем случае, уравнение имеет вид:
. В нашем случае, уравнение имеет вид:
 , а
, а  .
. :
: ,
,

 является первым интегралом уравнения. Т.к. он является суммой кинетической
является первым интегралом уравнения. Т.к. он является суммой кинетической  и потенциальной
и потенциальной  энергии системы, этот интеграл называется интегралом энергии данной системы.
энергии системы, этот интеграл называется интегралом энергии данной системы. , мы получаем эквивалентную исходному уравнению систему:
, мы получаем эквивалентную исходному уравнению систему:

 :
: , или
, или 
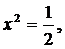

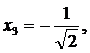

 :
: ;
;

 .
. .
.
 - точка типа «седло».
- точка типа «седло». и
и  - точки типа «центр».
- точки типа «центр».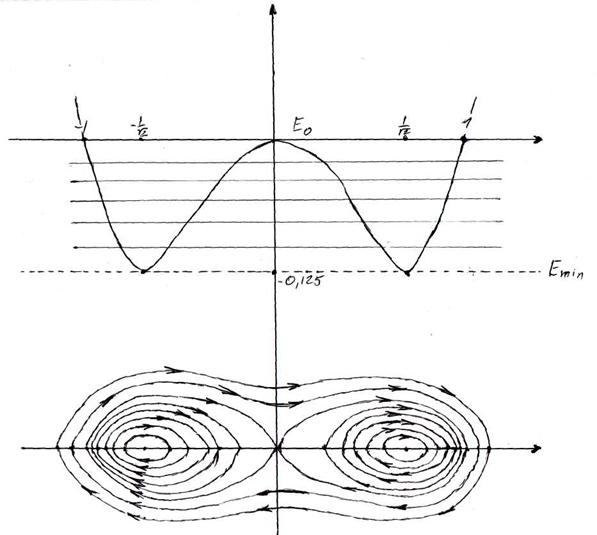




 T+ и T- соответственно.
T+ и T- соответственно.




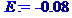



















 асимптотически устойчиво нулевое решение уравнения.
асимптотически устойчиво нулевое решение уравнения.
 ,
,  ,
,  ,
,  ,
,  .
.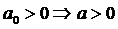


 .
.





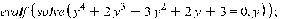


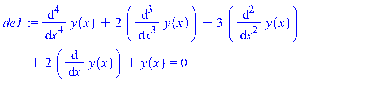





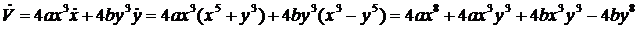
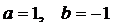 . Функция Ляпунова и ее производная в силу системы будут иметь вид:
. Функция Ляпунова и ее производная в силу системы будут иметь вид:

 – положение равновесия системы
– положение равновесия системы 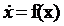 . Пусть
. Пусть  - непрерывно дифференцируемая функция, такая что
- непрерывно дифференцируемая функция, такая что 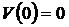 и
и  для некоторой точки
для некоторой точки  , такой что
, такой что  - произвольно малая величина. Определим множество
- произвольно малая величина. Определим множество  , и предположим что
, и предположим что  в
в  . Тогда,
. Тогда, 

